13.3.1 等腰三角形性质课件(23张PPT)
文档属性
| 名称 | 13.3.1 等腰三角形性质课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 17:47:44 | ||
图片预览



文档简介
(共23张PPT)
13.3.1 等腰三角形性质
华师大版 八年级上册
教学目标
1.使学生掌握等腰三角形的性质(等边对等角和三线合一).
2.使学生掌握等边三角形的性质.
【教学重点】等腰三角形的性质.
【教学难点】等腰三角形性质的探索.
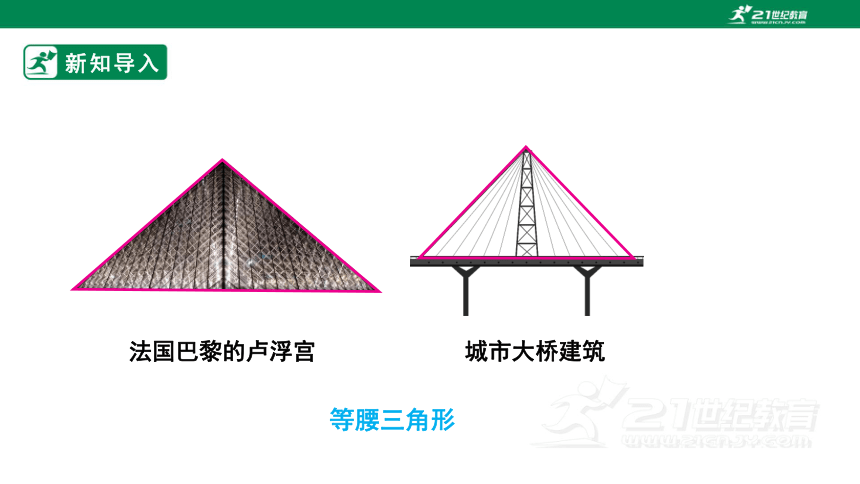
新知导入
法国巴黎的卢浮宫
城市大桥建筑
等腰三角形
新知讲解
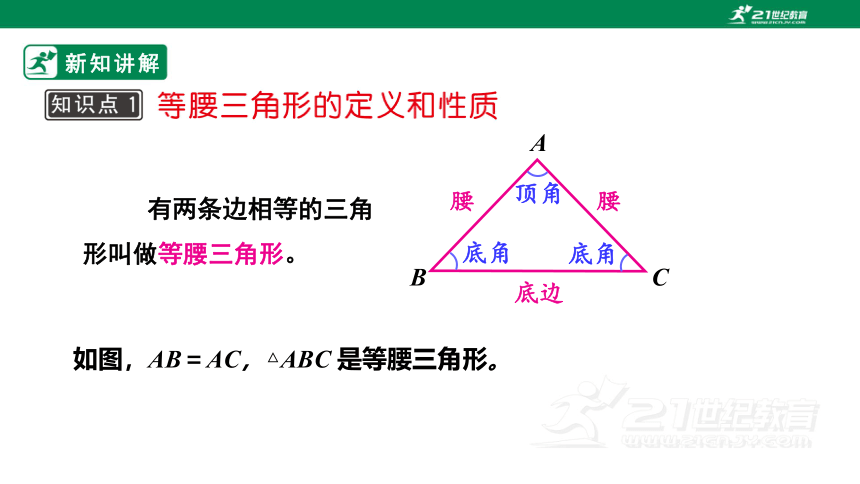
有两条边相等的三角形叫做等腰三角形。
A
B
C
如图,AB=AC,△ABC 是等腰三角形。
腰
腰
底边
顶角
底角
底角
巩固练习
1.填空:
(1)如果等腰三角形的一个底角为50°,那么其余两个角的大小分别为_____和______;
(2)如果等腰三角形的顶角为80°,那么它的一个底角的大小为______.
50°
80°
50°
新知讲解
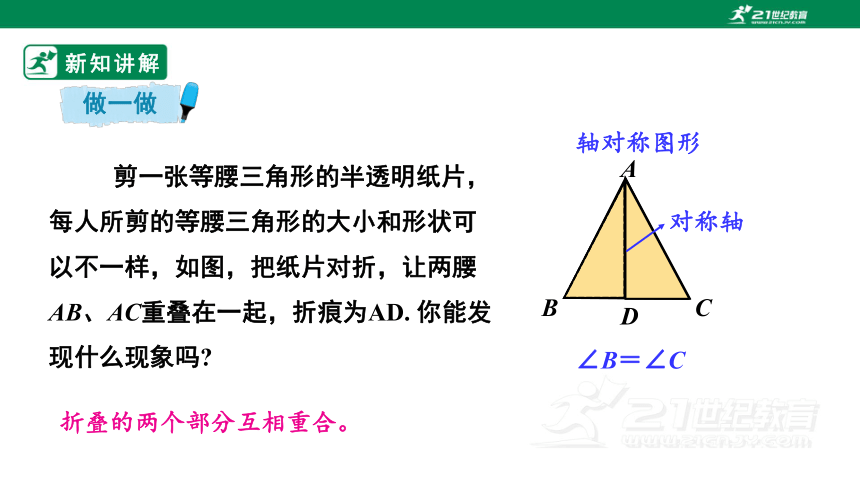
做一做
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD. 你能发现什么现象吗
A
B
C
D
折叠的两个部分互相重合。
轴对称图形
对称轴
∠B=∠C
新知讲解
A
B
C
D
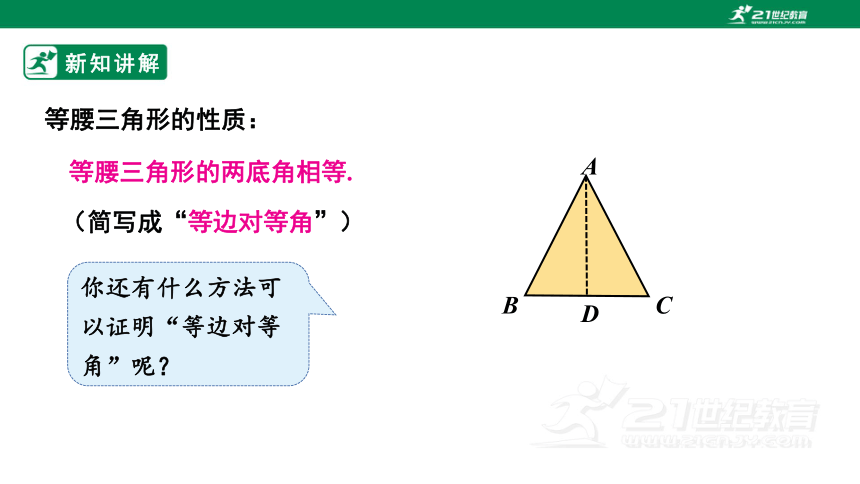
等腰三角形的性质:
等腰三角形的两底角相等.
(简写成“等边对等角”)
你还有什么方法可以证明“等边对等角”呢?
新知讲解
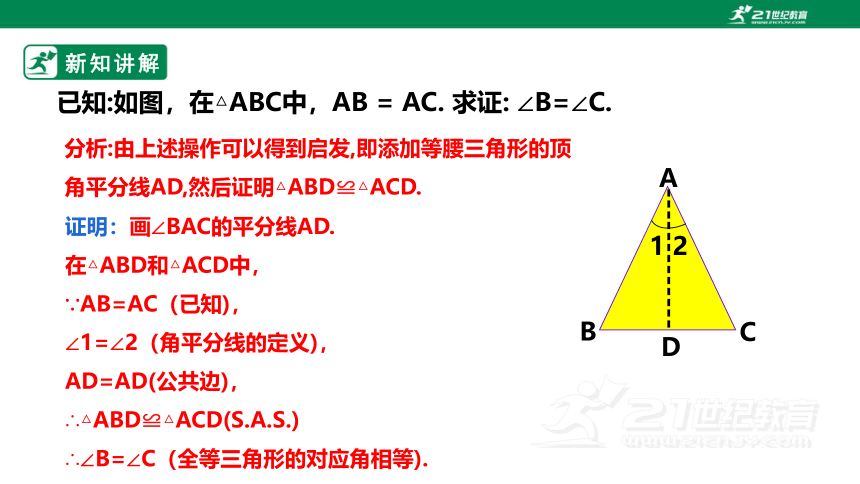
已知:如图,在△ABC中,AB = AC. 求证: ∠B=∠C.
分析:由上述操作可以得到启发,即添加等腰三角形的顶角平分线AD,然后证明△ABD≌△ACD.
-------------
A
C
B
D
1 2
证明:画∠BAC的平分线AD.
在△ABD和△ACD中,
∵AB=AC(已知),
∠1=∠2(角平分线的定义),
AD=AD(公共边),
∴△ABD≌△ACD(S.A.S.)
∴∠B=∠C(全等三角形的对应角相等).
新知讲解
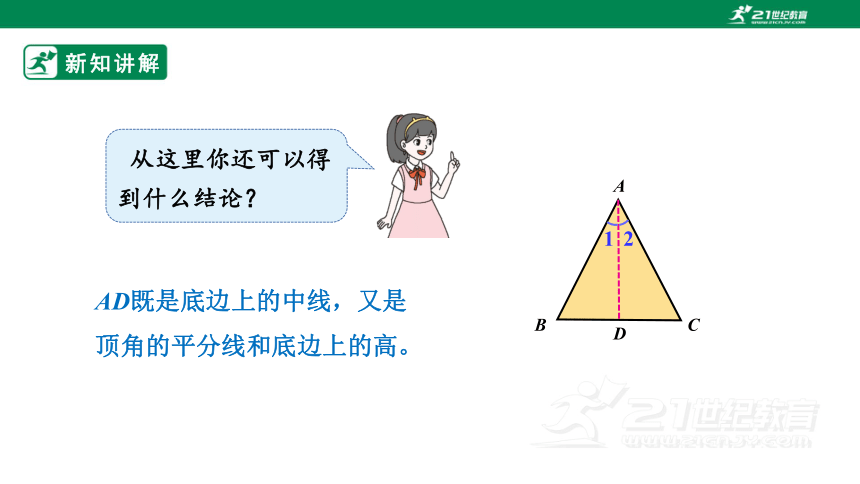
从这里你还可以得到什么结论?
A
B
C
D
1
2
AD既是底边上的中线,又是顶角的平分线和底边上的高。
例题讲解
解: ∵ AB=AC(已知),
∴∠C=∠B=80(等边对等角).
又∵ ∠ A+ ∠ B+ ∠ C=180°(三角形的内角和等于180°),
∴∠ A =180°- ∠ B- ∠ C(等式的性质)
=180°- 80°- 80°= 20°.
例1 已知:在△ABC中,AB=AC,∠B=80°.求∠C和∠A的大小.
例题讲解
例2 如图,在△ABC中,AB = AC,D是BC边上的中点,∠ B= 30°.求:∠ ADC的大小;(2)∠1的大小.
A
C
B
D
1 2
解:(1) ∵ AB= AC,BD = DC(已知),
∴AD⊥BC(等腰三角形的“三线合一”),
∴∠ ADC= ∠ ADB= 90°.
(2)∵ ∠ 1+ ∠ B + ∠ ADB = 180°
(三角形的内角和等于180°),
∠ B = 30°(已知),
∴∠ 1= 180° - ∠ B - ∠ ADB(等式的性质)
= 180°- 30°- 90°= 60°.
等腰三角形的“三线合一”是经常会用到的重要性质.
巩固练习
2. 如图,点E在BC上,AE// DC, AB = AE. 求证:∠B = ∠C.
A
D
C
E
B
证明:∵AE//DC,
∴∠C=∠AEB.
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠C.
新知讲解
A
B
C
等腰三角形
AB=AC
A
B
C
AB=AC=BC
等边三角形
新知讲解
A
B
C
AB=AC=BC
三条边都相等的三角形是等边三角形.
在等边三角形中,每个角的度数是多少呢?
新知讲解
A
B
C
显然,AB=AC,根据“等边对等角”,可以得到∠B=∠C
同理可得∠A=∠B
∴∠A=∠B=∠C
而∠A+∠B+∠C=180°
∴∠A=∠B=∠C=60°
等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的性质:
正三角形
例题讲解
例3 如图,△ABC是等边三角形,D是AC边上的中点,点E在BC的延长线上。若DE=BD,求∠CDE的度数.
巩固练习
3. 如图,△ABC是等边三角形,点D在AC上,∠DBC = 350,则∠ADB的度数为( ).
D
课堂总结
等腰三角形
底与腰不相等
定义
等边对等角→证明角相等
三线合一
底与腰相等→等边三角形
定义
等腰三角形的所有性质
特有性质:三边相等;三个角都等于60°
随堂练习
1. 有两个三角形,它们的三个角分别为:①20°, 40°,120°; ② 20°, 60°,100°. 怎样把它们分成两个等腰三角形 画出图形试试看.
如图所示:
随堂练习
2. 如图,AB = AC,D、E都是BC上的点,且BD = CE.求证:∠ADE = ∠AED.
证明:在△ABD和△ACE中
∵AB=AC ,∴∠B=∠C.
又∵BD=CE,
∴△ABD≌△ACE(S.A.S.)
∴AD=AE,
∴∠ADE=∠AED.
随堂练习
3. 如图,AB、CD相交于点E,EA =EC,AC// BD. 求证:EB = ED.
证明:∵EA=EC,
∴∠A=∠C.
∵AC // BD.
∴∠A=∠B,∠C=∠D,
∴∠B=∠D,
∴EB=ED.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.3.1 等腰三角形性质
华师大版 八年级上册
教学目标
1.使学生掌握等腰三角形的性质(等边对等角和三线合一).
2.使学生掌握等边三角形的性质.
【教学重点】等腰三角形的性质.
【教学难点】等腰三角形性质的探索.
新知导入
法国巴黎的卢浮宫
城市大桥建筑
等腰三角形
新知讲解
有两条边相等的三角形叫做等腰三角形。
A
B
C
如图,AB=AC,△ABC 是等腰三角形。
腰
腰
底边
顶角
底角
底角
巩固练习
1.填空:
(1)如果等腰三角形的一个底角为50°,那么其余两个角的大小分别为_____和______;
(2)如果等腰三角形的顶角为80°,那么它的一个底角的大小为______.
50°
80°
50°
新知讲解
做一做
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD. 你能发现什么现象吗
A
B
C
D
折叠的两个部分互相重合。
轴对称图形
对称轴
∠B=∠C
新知讲解
A
B
C
D
等腰三角形的性质:
等腰三角形的两底角相等.
(简写成“等边对等角”)
你还有什么方法可以证明“等边对等角”呢?
新知讲解
已知:如图,在△ABC中,AB = AC. 求证: ∠B=∠C.
分析:由上述操作可以得到启发,即添加等腰三角形的顶角平分线AD,然后证明△ABD≌△ACD.
-------------
A
C
B
D
1 2
证明:画∠BAC的平分线AD.
在△ABD和△ACD中,
∵AB=AC(已知),
∠1=∠2(角平分线的定义),
AD=AD(公共边),
∴△ABD≌△ACD(S.A.S.)
∴∠B=∠C(全等三角形的对应角相等).
新知讲解
从这里你还可以得到什么结论?
A
B
C
D
1
2
AD既是底边上的中线,又是顶角的平分线和底边上的高。
例题讲解
解: ∵ AB=AC(已知),
∴∠C=∠B=80(等边对等角).
又∵ ∠ A+ ∠ B+ ∠ C=180°(三角形的内角和等于180°),
∴∠ A =180°- ∠ B- ∠ C(等式的性质)
=180°- 80°- 80°= 20°.
例1 已知:在△ABC中,AB=AC,∠B=80°.求∠C和∠A的大小.
例题讲解
例2 如图,在△ABC中,AB = AC,D是BC边上的中点,∠ B= 30°.求:∠ ADC的大小;(2)∠1的大小.
A
C
B
D
1 2
解:(1) ∵ AB= AC,BD = DC(已知),
∴AD⊥BC(等腰三角形的“三线合一”),
∴∠ ADC= ∠ ADB= 90°.
(2)∵ ∠ 1+ ∠ B + ∠ ADB = 180°
(三角形的内角和等于180°),
∠ B = 30°(已知),
∴∠ 1= 180° - ∠ B - ∠ ADB(等式的性质)
= 180°- 30°- 90°= 60°.
等腰三角形的“三线合一”是经常会用到的重要性质.
巩固练习
2. 如图,点E在BC上,AE// DC, AB = AE. 求证:∠B = ∠C.
A
D
C
E
B
证明:∵AE//DC,
∴∠C=∠AEB.
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠C.
新知讲解
A
B
C
等腰三角形
AB=AC
A
B
C
AB=AC=BC
等边三角形
新知讲解
A
B
C
AB=AC=BC
三条边都相等的三角形是等边三角形.
在等边三角形中,每个角的度数是多少呢?
新知讲解
A
B
C
显然,AB=AC,根据“等边对等角”,可以得到∠B=∠C
同理可得∠A=∠B
∴∠A=∠B=∠C
而∠A+∠B+∠C=180°
∴∠A=∠B=∠C=60°
等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的性质:
正三角形
例题讲解
例3 如图,△ABC是等边三角形,D是AC边上的中点,点E在BC的延长线上。若DE=BD,求∠CDE的度数.
巩固练习
3. 如图,△ABC是等边三角形,点D在AC上,∠DBC = 350,则∠ADB的度数为( ).
D
课堂总结
等腰三角形
底与腰不相等
定义
等边对等角→证明角相等
三线合一
底与腰相等→等边三角形
定义
等腰三角形的所有性质
特有性质:三边相等;三个角都等于60°
随堂练习
1. 有两个三角形,它们的三个角分别为:①20°, 40°,120°; ② 20°, 60°,100°. 怎样把它们分成两个等腰三角形 画出图形试试看.
如图所示:
随堂练习
2. 如图,AB = AC,D、E都是BC上的点,且BD = CE.求证:∠ADE = ∠AED.
证明:在△ABD和△ACE中
∵AB=AC ,∴∠B=∠C.
又∵BD=CE,
∴△ABD≌△ACE(S.A.S.)
∴AD=AE,
∴∠ADE=∠AED.
随堂练习
3. 如图,AB、CD相交于点E,EA =EC,AC// BD. 求证:EB = ED.
证明:∵EA=EC,
∴∠A=∠C.
∵AC // BD.
∴∠A=∠B,∠C=∠D,
∴∠B=∠D,
∴EB=ED.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
