13.2.5 全等三角形-边边边课件(20张ppt)
文档属性
| 名称 | 13.2.5 全等三角形-边边边课件(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
13.2.5全等三角形-边边边
华师大版 八年级上册
教学目标
1、掌握S.S.S.判定两个三角形全等,会用S.A.S.、A.S.A.、A.A.S.、S.S.S.判定三角形全等.
2、会用S.S.S.判定两个三角形全等.(重点)
3、证明全等时,判定方法的选择.(难点)
复习导入
问题:目前我们已经学习了几种三角形全等的判定方法?
3种,分别是S.A.S.、A.S.A.、A.A.S.
有两边和它们的夹角对应相等的两个三角形全等
有两角和它们的夹边对应相等的两个三角形全等
有两角和其中一角的对边对应相等的两个三角形全等
S.A.S.
A.S.A.
A.A.S.
新知讲解
如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
不一定,如下面的两个三角形就不全等。
如果将上面的三个角换成三条边,结果又如何呢?
新知讲解
如图,已知三条线段,试画一个三角形,使这三条线段分别为其三条边.
把你画的三角形与你同伴画的三角形进行比较,或将你画的三角形剪下,放到你同伴画的三角形上,看看是否完全重合. 所画的三角形都全等吗?
新知讲解
基本事实 三边分别相等的两个三角形全等.
简记为 S.S.S.(或边边边)
用符号语言表示为:
例如: 在△ABC 和△A′B′C′中,
若AB=A′B′,BC=B′C′,AC=A′C′,
则△ABC≌△A′B′C′ (S.S.S.)
典例讲解
例1、 如图,在四边形ABCD中,AD=CB,AB=CD.求证:∠B=∠D.
由于∠B和∠D分别属于△ABC 和△CDA,所以只需证明这两个三角形全等即可.
证明:在△ABC和△CDA中,
∵CB=AD,AB=CD(已知),
AC=CA(公共边)
∴△ABC≌△CDA(S.S.S. )
∴∠B =∠D
(全等三角形的对应角相等).
巩固练习
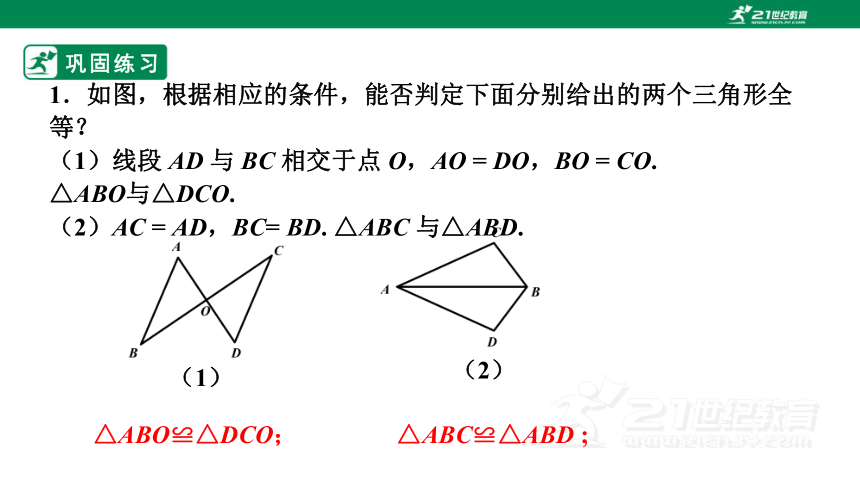
1.如图,根据相应的条件,能否判定下面分别给出的两个三角形全等?
(1)线段 AD 与 BC 相交于点 O,AO = DO,BO = CO.
△ABO与△DCO.
(2)AC = AD,BC= BD. △ABC 与△ABD.
△ABO≌△DCO;
△ABC≌△ABD ;
(1)
(2)
巩固练习
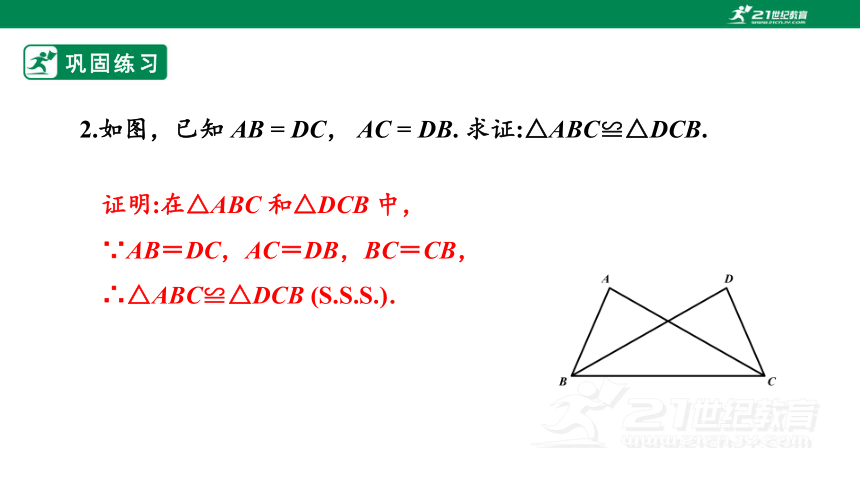
2.如图,已知 AB = DC, AC = DB. 求证:△ABC≌△DCB.
证明:在△ABC 和△DCB 中,
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB (S.S.S.).
巩固练习
3. 如图,点 B、E、C、F 在同一条直线上,AB = DE,AC = DF , BE = CF.求证:∠A = ∠D.并找出图中相互平行的线段,说明 你的理由.
证明:∵BE=CF,∴BE+CE=FC+EC,
∴BC=EF.在△ABC 和△DEF 中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF (S.S.S.),
∴∠A =∠D .AC∥DF.
因为∠ACB=∠DFE,
所以AC∥DF.AB∥DE.
因为∠B=∠DEF,所以 AB∥DE.
新知讲解
读
一
读
至此,我们已经学习了关于全等三角形的三个基本事实,这是进行演绎推理的重要依据. 它们是从静态的角度探索发现的判定方法,其本质与动态的全等三角形定义是一致的,即在这些条件下,两个三角形一定可以通过图形的基本变换 (轴对称、平移与旋转) 而相互重合.
新知讲解
概括
我们可以将前面关于全等三角形判定的探索得到的结论归纳成下表(请补充完整表格中的内容):
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边 三角形是否一定全等 一定 (S.A.S.) 一定 (A.S.A.)
不一定
(S.S.A.)
一定
(A.A.S.)
不一定
(A.A.A.)
一定
(S.S.S.)
例题讲解
例2、 如图,AB=CD,BC=DA,点E、F在AC上,且AE=CF求证:DE=BF.(方法的综合选择,一题多解)
巩固练习
4. 如图,在△ABC和△A’B’C’中,点D和点D’分别是BC和B’C’的中点,且AB=A’B’,BC=B’C’,AD=A’D’求证:△ABC≌△A’B’C’
课堂总结
边边边
判定定理
三边分别相等的两个三角形全等
应用
应用 S.S.S.判定三角形全等
三角形全等的判定方法的综合应用
随堂练习
1.如图,要使各对三角形全等,还需要增加什么条件?
(1)∠A =∠D,∠B = ∠F ;
(2)∠A =∠D,AB = DE.
(1)
(2)
解: (1)AB=DF (或AC=DE 或 BC=FE);
(2)∠B=∠E (或∠C=∠F 或 AC=DF).
随堂练习
2. 如图,已知 AB 与 CD 相交于点 O,∠A = ∠D,
CO = BO. 求证:△AOC≌△DOB.
证明: 在△AOC 和△DOB 中,
∵∠A =∠D ,∠AOC=∠DOB,
CO=BO,
∴△AOC≌△DOB (A.A.S.)
随堂练习
3. 如图,∠1 = ∠2,∠3 =∠4 . 求证: AB = AC.
证明: ∵∠3=∠4,
∴∠ADC=∠ADB.
在△ADC 和△ADB 中,
∵∠1=∠2,AD =AD,∠ADC=∠ADB,
∴△ADC≌△ADB (A.S.A.),
∴AB = AC.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.2.5全等三角形-边边边
华师大版 八年级上册
教学目标
1、掌握S.S.S.判定两个三角形全等,会用S.A.S.、A.S.A.、A.A.S.、S.S.S.判定三角形全等.
2、会用S.S.S.判定两个三角形全等.(重点)
3、证明全等时,判定方法的选择.(难点)
复习导入
问题:目前我们已经学习了几种三角形全等的判定方法?
3种,分别是S.A.S.、A.S.A.、A.A.S.
有两边和它们的夹角对应相等的两个三角形全等
有两角和它们的夹边对应相等的两个三角形全等
有两角和其中一角的对边对应相等的两个三角形全等
S.A.S.
A.S.A.
A.A.S.
新知讲解
如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
不一定,如下面的两个三角形就不全等。
如果将上面的三个角换成三条边,结果又如何呢?
新知讲解
如图,已知三条线段,试画一个三角形,使这三条线段分别为其三条边.
把你画的三角形与你同伴画的三角形进行比较,或将你画的三角形剪下,放到你同伴画的三角形上,看看是否完全重合. 所画的三角形都全等吗?
新知讲解
基本事实 三边分别相等的两个三角形全等.
简记为 S.S.S.(或边边边)
用符号语言表示为:
例如: 在△ABC 和△A′B′C′中,
若AB=A′B′,BC=B′C′,AC=A′C′,
则△ABC≌△A′B′C′ (S.S.S.)
典例讲解
例1、 如图,在四边形ABCD中,AD=CB,AB=CD.求证:∠B=∠D.
由于∠B和∠D分别属于△ABC 和△CDA,所以只需证明这两个三角形全等即可.
证明:在△ABC和△CDA中,
∵CB=AD,AB=CD(已知),
AC=CA(公共边)
∴△ABC≌△CDA(S.S.S. )
∴∠B =∠D
(全等三角形的对应角相等).
巩固练习
1.如图,根据相应的条件,能否判定下面分别给出的两个三角形全等?
(1)线段 AD 与 BC 相交于点 O,AO = DO,BO = CO.
△ABO与△DCO.
(2)AC = AD,BC= BD. △ABC 与△ABD.
△ABO≌△DCO;
△ABC≌△ABD ;
(1)
(2)
巩固练习
2.如图,已知 AB = DC, AC = DB. 求证:△ABC≌△DCB.
证明:在△ABC 和△DCB 中,
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB (S.S.S.).
巩固练习
3. 如图,点 B、E、C、F 在同一条直线上,AB = DE,AC = DF , BE = CF.求证:∠A = ∠D.并找出图中相互平行的线段,说明 你的理由.
证明:∵BE=CF,∴BE+CE=FC+EC,
∴BC=EF.在△ABC 和△DEF 中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF (S.S.S.),
∴∠A =∠D .AC∥DF.
因为∠ACB=∠DFE,
所以AC∥DF.AB∥DE.
因为∠B=∠DEF,所以 AB∥DE.
新知讲解
读
一
读
至此,我们已经学习了关于全等三角形的三个基本事实,这是进行演绎推理的重要依据. 它们是从静态的角度探索发现的判定方法,其本质与动态的全等三角形定义是一致的,即在这些条件下,两个三角形一定可以通过图形的基本变换 (轴对称、平移与旋转) 而相互重合.
新知讲解
概括
我们可以将前面关于全等三角形判定的探索得到的结论归纳成下表(请补充完整表格中的内容):
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边 三角形是否一定全等 一定 (S.A.S.) 一定 (A.S.A.)
不一定
(S.S.A.)
一定
(A.A.S.)
不一定
(A.A.A.)
一定
(S.S.S.)
例题讲解
例2、 如图,AB=CD,BC=DA,点E、F在AC上,且AE=CF求证:DE=BF.(方法的综合选择,一题多解)
巩固练习
4. 如图,在△ABC和△A’B’C’中,点D和点D’分别是BC和B’C’的中点,且AB=A’B’,BC=B’C’,AD=A’D’求证:△ABC≌△A’B’C’
课堂总结
边边边
判定定理
三边分别相等的两个三角形全等
应用
应用 S.S.S.判定三角形全等
三角形全等的判定方法的综合应用
随堂练习
1.如图,要使各对三角形全等,还需要增加什么条件?
(1)∠A =∠D,∠B = ∠F ;
(2)∠A =∠D,AB = DE.
(1)
(2)
解: (1)AB=DF (或AC=DE 或 BC=FE);
(2)∠B=∠E (或∠C=∠F 或 AC=DF).
随堂练习
2. 如图,已知 AB 与 CD 相交于点 O,∠A = ∠D,
CO = BO. 求证:△AOC≌△DOB.
证明: 在△AOC 和△DOB 中,
∵∠A =∠D ,∠AOC=∠DOB,
CO=BO,
∴△AOC≌△DOB (A.A.S.)
随堂练习
3. 如图,∠1 = ∠2,∠3 =∠4 . 求证: AB = AC.
证明: ∵∠3=∠4,
∴∠ADC=∠ADB.
在△ADC 和△ADB 中,
∵∠1=∠2,AD =AD,∠ADC=∠ADB,
∴△ADC≌△ADB (A.S.A.),
∴AB = AC.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
