13.2.6 全等三角形 -斜边直角边课件(26张ppt)
文档属性
| 名称 | 13.2.6 全等三角形 -斜边直角边课件(26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 17:52:10 | ||
图片预览






文档简介
(共26张PPT)
13.2.6 全等三角形 -斜边直角边
华师大版 八年级上册
教学目标
1.会用“H.L.”判定两个直角三角形全等.(重点)
2.会综合用各种方法判定两个直角三角形全等.(难点)
新知导入
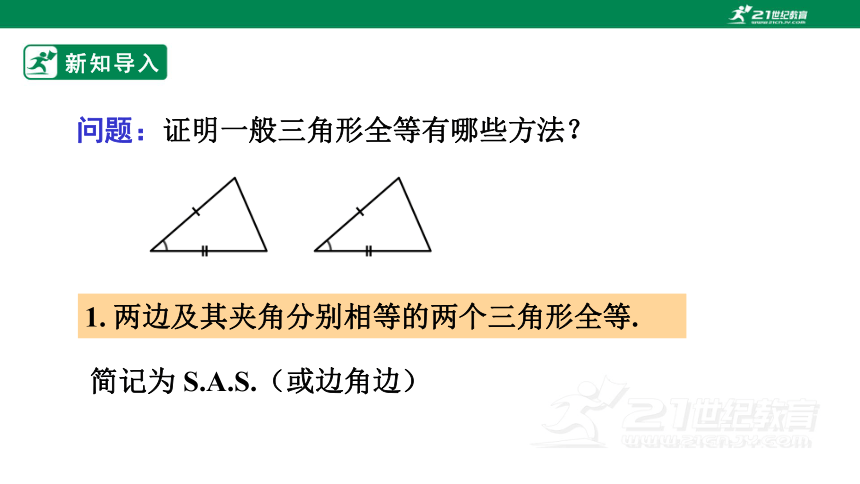
问题:证明一般三角形全等有哪些方法?
1. 两边及其夹角分别相等的两个三角形全等.
简记为 S.A.S.(或边角边)
新知讲解
2.两角及其夹边分别相等的两个三角形全等.
简记为 A.S.A.(或角边角)
新知讲解
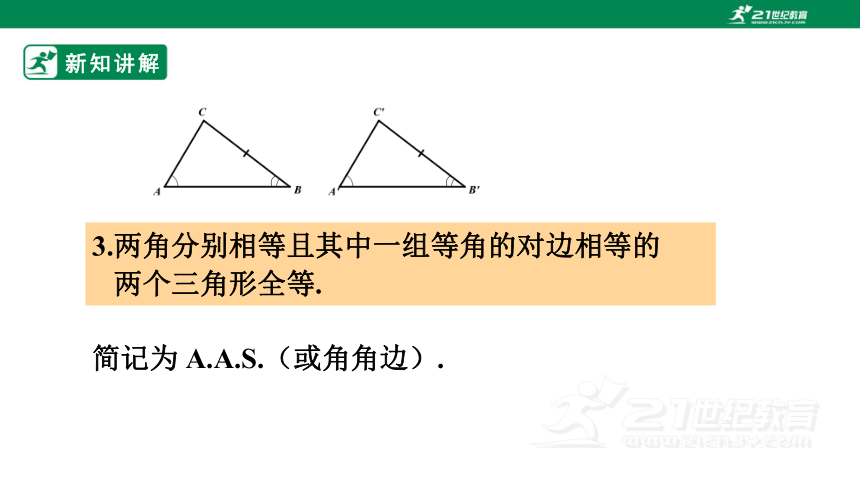
3.两角分别相等且其中一组等角的对边相等的
两个三角形全等.
简记为 A.A.S.(或角角边).
新知讲解
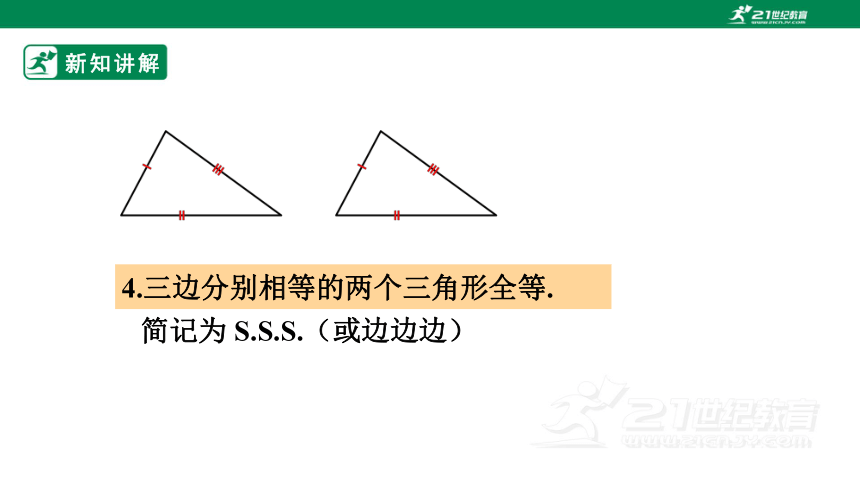
4.三边分别相等的两个三角形全等.
简记为 S.S.S.(或边边边)
新知讲解
我们已经知道,对于两个三角形,如果有“边边角”分别对应相等,那么不能保证这两个三角形全等.
在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形是否全等呢?
新知讲解
如图,已知两条线段(这两条线段长不相等),试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.
新知讲解
步骤:
1.画一条线段AB,使它等于 2 cm;
2.画∠MAB = 90°(用量角器或三角尺);
3.以点 B 为圆心、3 cm 长为半径画圆弧,交射线 AM于点C;
4.连结 BC.
△ABC 即为所求.
新知讲解
把你画的直角三角形与其他同学画的直角三角形进行比较,或将你画的直角三角形剪下,放到其他同学画的直角三角形上,看看是否完全重合. 所画的直角三角形都全等吗?
换两条线段,试试看,是否有同样的结论?
新知讲解
斜边和一条直角边分别相等的两个直角三角形全等.
简记为 H.L.(或斜边直角边).
典例讲解
例1、如图,已知AC=BD,∠C=∠D=90°.
求证:BC = AD.
由于AD与BC分别属于△BAD和△ABC,所以只需证明这两个三角形全等即可.
典例讲解
证明:∵∠C=∠D=90°(已知)
∴△ABC与△BAD都是直角三角形
(直角三角形的定义).
在Rt△ABC与Rt△BAD中,
∵AB=BA(公共边),AC=BD(已知),
∴Rt△ABC≌Rt△BAD(H.L. )
∴BC=AD(全等三角形的对应边相等).
直角三角形可以用符号“Rt△”来表示.
新知讲解
1. 一般三角形的全等与直角三角形的全等是从一般到特殊的关系,二者之间的联系为: 一般三角形的判定方法同样适用于直角三角形.
2.判定一般三角形的全等与直角三角形的全等的区别:
(1)一般三角形全等的条件“S.S.S.”在直角三角形中被“H.L.”代替,无需找第三条边对应相等;
(2)“两边及其中一边的对角对应相等”不能判定一般三角形全等,但能判定直角三角形全等.
巩固练习
如图,在△ABC中,D为 BC 的中点,DE⊥AB,DF⊥AC,点 E、F 为垂足,DE = DF. 求证:△BED≌△CFD.
证明: ∵ DE ⊥ AB,DF ⊥ AC,
∴ ∠BED = ∠CFD = 90°,
∴△BED 与△CFD 都是直角三角形.
∵D 为 BC 的中点,
∴BD = CD .
在 Rt△BED 与 Rt△CFD 中,
∵BD = CD ,DE = DF,
∴Rt△BED ≌Rt△CFD (H.L.).
巩固练习
2. 如图,AC = AD,∠C =∠D = 90°.求证: BC = BD.
证明:在Rt△ACB 和Rt△ADB 中,
∵AB=AB,AC=AD ,
∴Rt△ACB≌Rt△ADB (H.L.).
∴BC = BD .
巩固练习
如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的跨度 DF 相等,两个滑梯的倾斜角∠B 与 ∠F 的大小有什么关系?说说你的想法和理由.
解: ∠B+∠F = 90°.
可以利用已知条件证明
Rt△ABC ≌Rt△DEF (H.L.),
∴∠B =∠DEF,
∴∠B+∠F = 90°.
典例讲解
例2、如图,在中Rt△ACB,∠C=900,AC=10,BC=5,AG⊥AC于A,点P,点Q分别在线段AC和射线AG上运动,且PQ=AB.当点P运动到线段AC上什么位置时,△APQ和△ABC全等
解题策略:当题目中遇到用文字表示的全等中,要分类讨论,避免出错
课堂总结
斜边直角边
判定定理
形式
斜边和一条直角边分别相等的两个直角三角形全等
H.L.(斜边直角边),存在于直角三角形中
判定直角三角形全等与判定一般三角形全等的联系与区别
应用
用H.L.解决问题
拓展提高
拓展提高
拓展提高
拓展提高
拓展提高
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.2.6 全等三角形 -斜边直角边
华师大版 八年级上册
教学目标
1.会用“H.L.”判定两个直角三角形全等.(重点)
2.会综合用各种方法判定两个直角三角形全等.(难点)
新知导入
问题:证明一般三角形全等有哪些方法?
1. 两边及其夹角分别相等的两个三角形全等.
简记为 S.A.S.(或边角边)
新知讲解
2.两角及其夹边分别相等的两个三角形全等.
简记为 A.S.A.(或角边角)
新知讲解
3.两角分别相等且其中一组等角的对边相等的
两个三角形全等.
简记为 A.A.S.(或角角边).
新知讲解
4.三边分别相等的两个三角形全等.
简记为 S.S.S.(或边边边)
新知讲解
我们已经知道,对于两个三角形,如果有“边边角”分别对应相等,那么不能保证这两个三角形全等.
在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形是否全等呢?
新知讲解
如图,已知两条线段(这两条线段长不相等),试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.
新知讲解
步骤:
1.画一条线段AB,使它等于 2 cm;
2.画∠MAB = 90°(用量角器或三角尺);
3.以点 B 为圆心、3 cm 长为半径画圆弧,交射线 AM于点C;
4.连结 BC.
△ABC 即为所求.
新知讲解
把你画的直角三角形与其他同学画的直角三角形进行比较,或将你画的直角三角形剪下,放到其他同学画的直角三角形上,看看是否完全重合. 所画的直角三角形都全等吗?
换两条线段,试试看,是否有同样的结论?
新知讲解
斜边和一条直角边分别相等的两个直角三角形全等.
简记为 H.L.(或斜边直角边).
典例讲解
例1、如图,已知AC=BD,∠C=∠D=90°.
求证:BC = AD.
由于AD与BC分别属于△BAD和△ABC,所以只需证明这两个三角形全等即可.
典例讲解
证明:∵∠C=∠D=90°(已知)
∴△ABC与△BAD都是直角三角形
(直角三角形的定义).
在Rt△ABC与Rt△BAD中,
∵AB=BA(公共边),AC=BD(已知),
∴Rt△ABC≌Rt△BAD(H.L. )
∴BC=AD(全等三角形的对应边相等).
直角三角形可以用符号“Rt△”来表示.
新知讲解
1. 一般三角形的全等与直角三角形的全等是从一般到特殊的关系,二者之间的联系为: 一般三角形的判定方法同样适用于直角三角形.
2.判定一般三角形的全等与直角三角形的全等的区别:
(1)一般三角形全等的条件“S.S.S.”在直角三角形中被“H.L.”代替,无需找第三条边对应相等;
(2)“两边及其中一边的对角对应相等”不能判定一般三角形全等,但能判定直角三角形全等.
巩固练习
如图,在△ABC中,D为 BC 的中点,DE⊥AB,DF⊥AC,点 E、F 为垂足,DE = DF. 求证:△BED≌△CFD.
证明: ∵ DE ⊥ AB,DF ⊥ AC,
∴ ∠BED = ∠CFD = 90°,
∴△BED 与△CFD 都是直角三角形.
∵D 为 BC 的中点,
∴BD = CD .
在 Rt△BED 与 Rt△CFD 中,
∵BD = CD ,DE = DF,
∴Rt△BED ≌Rt△CFD (H.L.).
巩固练习
2. 如图,AC = AD,∠C =∠D = 90°.求证: BC = BD.
证明:在Rt△ACB 和Rt△ADB 中,
∵AB=AB,AC=AD ,
∴Rt△ACB≌Rt△ADB (H.L.).
∴BC = BD .
巩固练习
如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的跨度 DF 相等,两个滑梯的倾斜角∠B 与 ∠F 的大小有什么关系?说说你的想法和理由.
解: ∠B+∠F = 90°.
可以利用已知条件证明
Rt△ABC ≌Rt△DEF (H.L.),
∴∠B =∠DEF,
∴∠B+∠F = 90°.
典例讲解
例2、如图,在中Rt△ACB,∠C=900,AC=10,BC=5,AG⊥AC于A,点P,点Q分别在线段AC和射线AG上运动,且PQ=AB.当点P运动到线段AC上什么位置时,△APQ和△ABC全等
解题策略:当题目中遇到用文字表示的全等中,要分类讨论,避免出错
课堂总结
斜边直角边
判定定理
形式
斜边和一条直角边分别相等的两个直角三角形全等
H.L.(斜边直角边),存在于直角三角形中
判定直角三角形全等与判定一般三角形全等的联系与区别
应用
用H.L.解决问题
拓展提高
拓展提高
拓展提高
拓展提高
拓展提高
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
