2022-2023学年人教版数学八年级上册12.2全等三角形的判定 课件-(共19张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册12.2全等三角形的判定 课件-(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 20:19:36 | ||
图片预览


文档简介
(共19张PPT)
12.2 全等三角形的判定
1
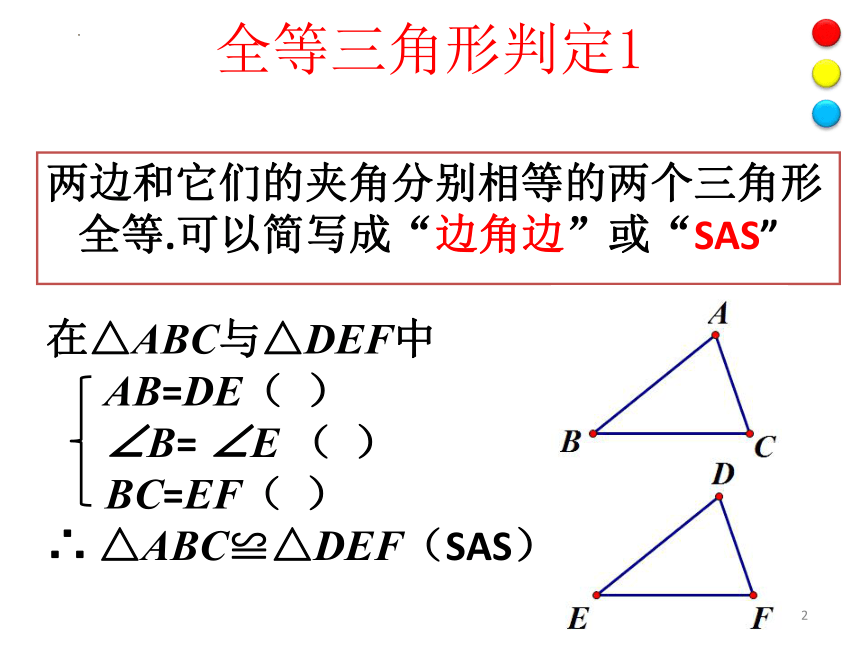
全等三角形判定1
两边和它们的夹角分别相等的两个三角形全等.可以简写成“边角边”或“SAS”
2
在△ABC与△DEF中
AB=DE( )
∠B= ∠E ( )
BC=EF( )
∴ △ABC≌△DEF(SAS)
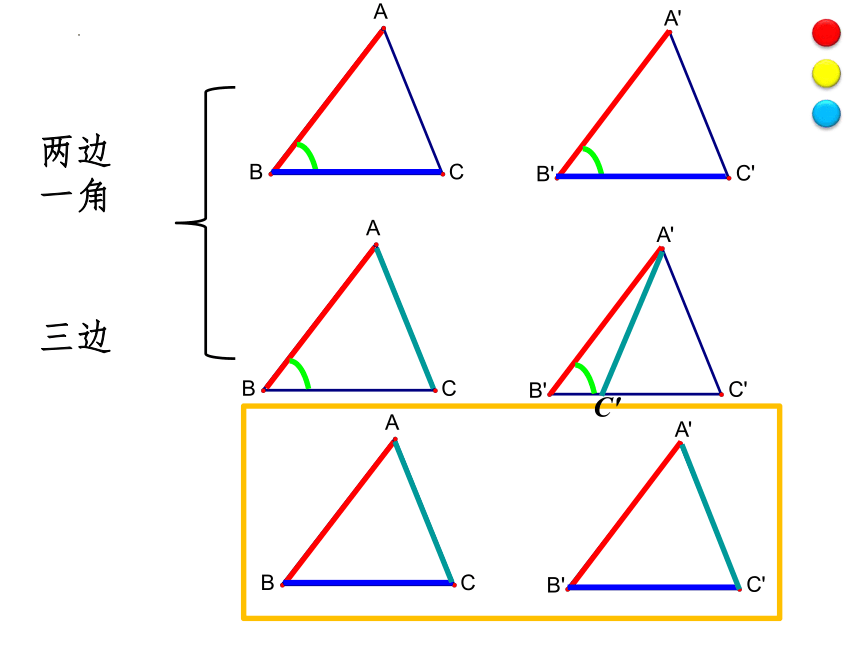
两边
一角
三边
C′
操作画图,验证猜想
先任意画出一个△ABC,再画出一个△A′B′C′,
使A′B′= AB,B′C′= BC,A′C′= AC.它们全等吗?
发现:△ABC≌△A′B′C′
5
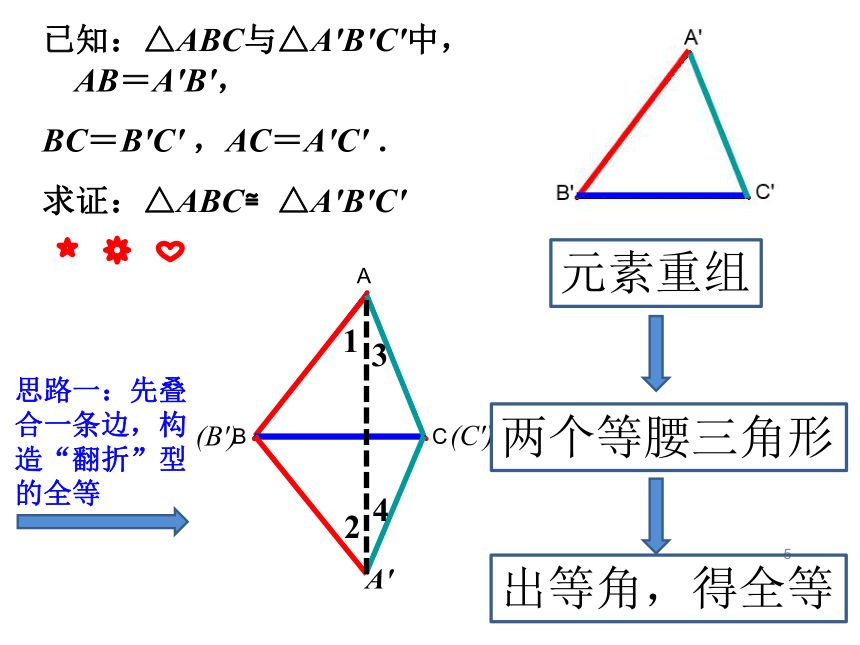
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
A′
(B′)
(C′)
思路一:先叠合一条边,构造“翻折”型的全等
元素重组
两个等腰三角形
出等角,得全等
1
2
3
4
2022/10/2
6
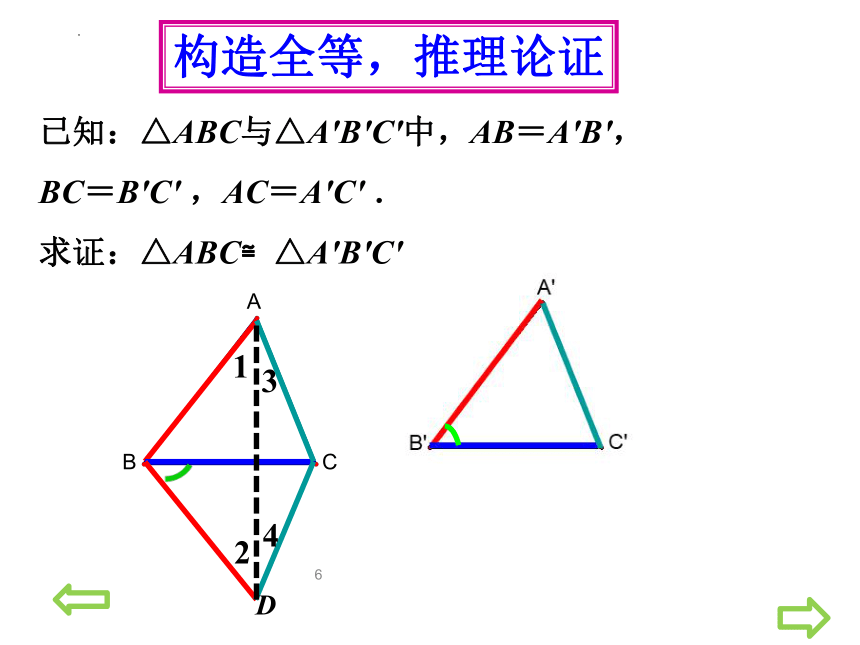
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
D
1
2
3
4
构造全等,推理论证
思路二:先叠合一条边,构造“旋转”型的全等
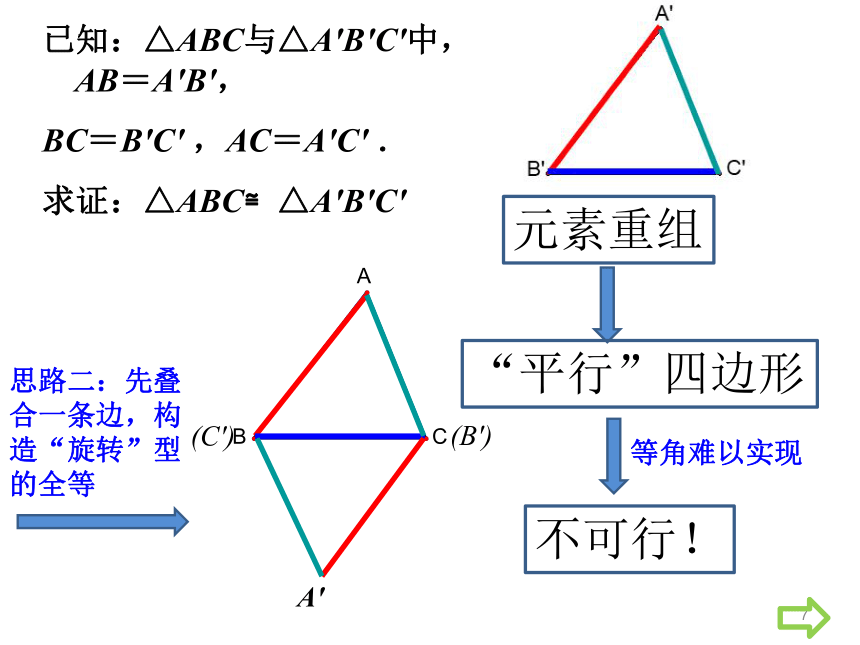
7
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
A′
(C′)
(B′)
元素重组
“平行”四边形
不可行!
等角难以实现
思路三:先叠合一条边,构造“完全重合”型的全等
8
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
A′
(B′)
(C′)
思路四:先叠合一条边,构造同侧“轴对称”型的全等
9
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
A′
(C′)
(B′)
全等三角形判定2
三边分别相等的两个三角形全等.
可以简写成“边边边”或“SSS”
10
在△ABC与△DEF中
AB=DE( )
AC=DF( )
BC=EF( )
∴ △ABC≌△DEF(SSS)
11
三角形具有稳定性
“SSS”
形状、大小唯一确定
三边长度确定
三边分别相等
两个三角形全等
一个三角形
两个三角形
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例1. 用尺规作一个角等于已知角.并说明作图原理。
O
D
B
C
A
应用定理,解决问题
作法:
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
O′
C′
A′
O
D
B
C
A
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例1. 用尺规作一个角等于已知角.并说明作图原理。
作法:
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′;
O′
D′
C′
A′
O
D
B
C
A
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例1. 用尺规作一个角等于已知角.并说明作图原理。
作法:
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
O′
D′
B′
C′
A′
O
D
B
C
A
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例1. 用尺规作一个角等于已知角.并说明作图原理。
16
例2.两组邻边分别相等的四边形叫做筝形.
在四边形ABCD 中,AB =AD,
BC =DC,则四边形ABCD 是筝形 .
A
B
C
D
O
你能发现筝形ABCD有什么性质?
在筝形ABCD 中,
边:
角:
对角线:
17
17
A
B
C
D
O
猜想:
∠ABC =∠ADC
AB =AD,BC =DC
∠BAC =∠DAC,∠ACB =∠ACD ,
AC⊥BD,BO =DO
18
1.本节课我们探究了一个什么问题?
我们是采用什么思路得到的?
3.请你继续运用已学的方法和思路去探究
满足“两角一边”的情形.
2.在探究过程中你学到了哪些技巧与方法?
课堂小结,梳理提升
思维训练
19
已知:在Rt△ABC与Rt△A’B’C’中
∠B= ∠B’=90°,AC=A’C’, AB=A’B’
问:Rt△ABC 与Rt △A’B’C’全等吗?
12.2 全等三角形的判定
1
全等三角形判定1
两边和它们的夹角分别相等的两个三角形全等.可以简写成“边角边”或“SAS”
2
在△ABC与△DEF中
AB=DE( )
∠B= ∠E ( )
BC=EF( )
∴ △ABC≌△DEF(SAS)
两边
一角
三边
C′
操作画图,验证猜想
先任意画出一个△ABC,再画出一个△A′B′C′,
使A′B′= AB,B′C′= BC,A′C′= AC.它们全等吗?
发现:△ABC≌△A′B′C′
5
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
A′
(B′)
(C′)
思路一:先叠合一条边,构造“翻折”型的全等
元素重组
两个等腰三角形
出等角,得全等
1
2
3
4
2022/10/2
6
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
D
1
2
3
4
构造全等,推理论证
思路二:先叠合一条边,构造“旋转”型的全等
7
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
A′
(C′)
(B′)
元素重组
“平行”四边形
不可行!
等角难以实现
思路三:先叠合一条边,构造“完全重合”型的全等
8
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
A′
(B′)
(C′)
思路四:先叠合一条边,构造同侧“轴对称”型的全等
9
已知:△ABC与△A′B′C′中,AB=A′B′,
BC=B′C′ ,AC=A′C′ .
求证:△ABC≌△A′B′C′
A′
(C′)
(B′)
全等三角形判定2
三边分别相等的两个三角形全等.
可以简写成“边边边”或“SSS”
10
在△ABC与△DEF中
AB=DE( )
AC=DF( )
BC=EF( )
∴ △ABC≌△DEF(SSS)
11
三角形具有稳定性
“SSS”
形状、大小唯一确定
三边长度确定
三边分别相等
两个三角形全等
一个三角形
两个三角形
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例1. 用尺规作一个角等于已知角.并说明作图原理。
O
D
B
C
A
应用定理,解决问题
作法:
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
O′
C′
A′
O
D
B
C
A
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例1. 用尺规作一个角等于已知角.并说明作图原理。
作法:
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′;
O′
D′
C′
A′
O
D
B
C
A
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例1. 用尺规作一个角等于已知角.并说明作图原理。
作法:
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
O′
D′
B′
C′
A′
O
D
B
C
A
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例1. 用尺规作一个角等于已知角.并说明作图原理。
16
例2.两组邻边分别相等的四边形叫做筝形.
在四边形ABCD 中,AB =AD,
BC =DC,则四边形ABCD 是筝形 .
A
B
C
D
O
你能发现筝形ABCD有什么性质?
在筝形ABCD 中,
边:
角:
对角线:
17
17
A
B
C
D
O
猜想:
∠ABC =∠ADC
AB =AD,BC =DC
∠BAC =∠DAC,∠ACB =∠ACD ,
AC⊥BD,BO =DO
18
1.本节课我们探究了一个什么问题?
我们是采用什么思路得到的?
3.请你继续运用已学的方法和思路去探究
满足“两角一边”的情形.
2.在探究过程中你学到了哪些技巧与方法?
课堂小结,梳理提升
思维训练
19
已知:在Rt△ABC与Rt△A’B’C’中
∠B= ∠B’=90°,AC=A’C’, AB=A’B’
问:Rt△ABC 与Rt △A’B’C’全等吗?
