数学人教A版(2019)必修第一册3.1.1 函数的概念(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.1.1 函数的概念(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 22:23:54 | ||
图片预览








文档简介
(共20张PPT)
新高考人教版(2019)必修第一册
§3.1.1 函数的概念
(1)初中学习的函数的定义是什么?
设在一个变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数.其中x叫自变量,y叫因变量.
复习回顾
一
(2)一次函数、二次函数、反比例函数、正比例函数的通式
正方形的周长l与边长x之间的关系:
一
(1)y=4x与正比例函数y=4x相同吗?
思考
(2)y=x与y=相同吗?
y=4x
问题1 某“复兴号”高速列车到350km/h后保持匀速运行半小时。这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为
情景导入
二
S =350t
不正确
情景导入
二
思考:根据对应关系S=350t,这趟列车加速到350km/h后,
运行1h就前进了350km,这个说法正确吗?
对应关系应为S=350t,其中,
情景导入
二
问题2:某电气维修告诉要求工人每周工作至少1天,至多不超过6天。如果公司确定的工资标准是每人每天350元,而且每周付一次工资,那么你认为该怎样确定一个工人每周的工资?一个工人的工资w(单位:元)是他工作天数d的函数吗?
是函数,对应关系为w=350d,其中,
在问题1和问题2中的函数有相同的对应关系,你认为它们是同一个函数吗?为什么?
一
思考
不是,自变量取值范围不同
情景导入
二
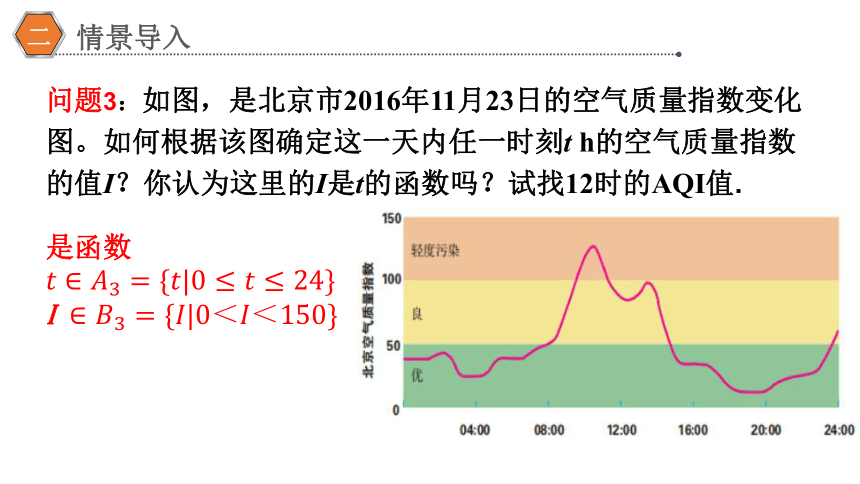
问题3:如图,是北京市2016年11月23日的空气质量指数变化图。如何根据该图确定这一天内任一时刻t h的空气质量指数的值I?你认为这里的I是t的函数吗?试找12时的AQI值.
是函数
I
情景导入
二
问题4:国际上常用恩格尔系数 r() 反映一个地区人民生活质量的高低,恩格尔系数越低,生活质量越高。上表是我国某省城镇居民恩格尔系数变化情况,从表中可以看出,该省城镇居民的生活质量越来越高。你认为该表给出的对应关系,恩格尔系数r是年份y的函数吗?
是函数
思考
问题情景 自变量的集合 对应 关系 函数值所在集合 函数值的集合
问题1 ={t|0≤t≤0.5} S=350t ={S|0≤S≤175}
问题2 ={1,2,3,4,5,6} w=350d ={350,700,1050,1400,1750,2100}
问题3 ={t|0≤t≤24} 图3.1-1 ={I|0<I<150}
问题4 ={2006,2007,...,2015} 表3.1-1 ={r|0上述问题1~问题4中的函数有哪些共同特征?由此你能概括出函数概念的本质特征吗?
上述问题1~问题4中的函数有哪些共同特征?由此你能概括出函数概念的本质特征吗?
一
思考
共同特征有:
(1)都包含两个非空数集,用A,B来表示;
(2)都有一个对应关系;
(3)尽管对应关系的表示方法不同,但它们都有如下特性:对于
数集A中的任意一个数x,按照对应关系,在数集B中都有唯一
确定的数y和它对应。
函数的概念
三
设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数(function),记作:
y=f(x),x∈A
x叫做自变量,x的取值范围A叫做函数的定义域(domain);
与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}
叫做函数的值域(range)
函数的值域与集合B什么关系?请你说出上述四个问题的值域?
函数的值域是集合B的子集.
问题1和问题2中,值域就是集合B1和B2;
问题3和问题4中,值域是B3和B4的真子集.
思考
函数的概念的理解
四
(1) 定义域、值域、对应关系是函数的三个要素,不可分割,其中对 应关系有多种形式,如:解析式、图像、表格、Venn图、文字形式
如:y=ax+b可以写成f (x)= ax+b;当x=1时y=2可以写成f (1)=2
(2) y=f(x)为“y是x的函数”的数学表示,仅是一个函数符号,不能理解为y等于f与x的乘积
(3)y=f (x)是函数符号,可用任意字母表示,如:y=g(x),y=h(x);
函数的概念的理解
四
(5)f (a)与f (x)有什么区别?
一般地,f(a)表示当x=a时的函数值,是一个常量
f(x)表示自变量x的函数,一般情况下是变量
(4) 判断y=f(x),x∈A与u=f(v),v∈A的异同
函数相等,则定义域与对应关系相同
y=x与y=相同吗?
y=x与y=相同吗?
练一练
1.对于函数y=f (x),以下说法正确的有( )
①y是x的函数 ②对于不同的x,y的值也不同
③ f(a)表示当x=a时函数f(x)的值,是一个常量
④ f(x)一定可以用一个具体的式子表示出来
A.1个 B.2个 C.3个 D.4个
B
练一练
2.试确定一次函数、二次函数、反比例函数的定义域和值域
函 数 一次函数 二次函数 反比例函数
a>0 a<0
对应关系
定义域
值 域
x→ax+b
x→ ax2+bx+c
y=ax+b(a≠0)
y=ax2+bx+c (a≠0)
R
R
R
{x|x≠0}
R
{y|y≠0}
(k≠0)
练一练
例1. 函数的解析式是舍弃问题的实际背景而抽象出来的,它所反映的两个量之间的对应关系,可以广泛地用于刻画同一类事物中的变量关系和规律。例如,正比例函数y=kx(k≠0)可以用来刻画匀速运动中的路程与时间的关系、一定密度的物体的质量与体积的关系、圆的周长与半径的关系等。试构建一个问题情境,使其中的变量关系可以用解析式y=x(10-x)来描述。
解:长方形的周长为20,设一边长为x,面积为y,那么y=x(10-x).
其中,x的取值范围是A={x|0对应关系f把每一个长方形的边长x,对应到唯一确定的面积x(10-x).
课堂小结
五
1. 函数的定义
2. 函数相等的条件
设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数(function),记作:
y=f(x),x∈A
作业
教材P63 1,2,3,4
新高考人教版(2019)必修第一册
§3.1.1 函数的概念
(1)初中学习的函数的定义是什么?
设在一个变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数.其中x叫自变量,y叫因变量.
复习回顾
一
(2)一次函数、二次函数、反比例函数、正比例函数的通式
正方形的周长l与边长x之间的关系:
一
(1)y=4x与正比例函数y=4x相同吗?
思考
(2)y=x与y=相同吗?
y=4x
问题1 某“复兴号”高速列车到350km/h后保持匀速运行半小时。这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为
情景导入
二
S =350t
不正确
情景导入
二
思考:根据对应关系S=350t,这趟列车加速到350km/h后,
运行1h就前进了350km,这个说法正确吗?
对应关系应为S=350t,其中,
情景导入
二
问题2:某电气维修告诉要求工人每周工作至少1天,至多不超过6天。如果公司确定的工资标准是每人每天350元,而且每周付一次工资,那么你认为该怎样确定一个工人每周的工资?一个工人的工资w(单位:元)是他工作天数d的函数吗?
是函数,对应关系为w=350d,其中,
在问题1和问题2中的函数有相同的对应关系,你认为它们是同一个函数吗?为什么?
一
思考
不是,自变量取值范围不同
情景导入
二
问题3:如图,是北京市2016年11月23日的空气质量指数变化图。如何根据该图确定这一天内任一时刻t h的空气质量指数的值I?你认为这里的I是t的函数吗?试找12时的AQI值.
是函数
I
情景导入
二
问题4:国际上常用恩格尔系数 r() 反映一个地区人民生活质量的高低,恩格尔系数越低,生活质量越高。上表是我国某省城镇居民恩格尔系数变化情况,从表中可以看出,该省城镇居民的生活质量越来越高。你认为该表给出的对应关系,恩格尔系数r是年份y的函数吗?
是函数
思考
问题情景 自变量的集合 对应 关系 函数值所在集合 函数值的集合
问题1 ={t|0≤t≤0.5} S=350t ={S|0≤S≤175}
问题2 ={1,2,3,4,5,6} w=350d ={350,700,1050,1400,1750,2100}
问题3 ={t|0≤t≤24} 图3.1-1 ={I|0<I<150}
问题4 ={2006,2007,...,2015} 表3.1-1 ={r|0
上述问题1~问题4中的函数有哪些共同特征?由此你能概括出函数概念的本质特征吗?
一
思考
共同特征有:
(1)都包含两个非空数集,用A,B来表示;
(2)都有一个对应关系;
(3)尽管对应关系的表示方法不同,但它们都有如下特性:对于
数集A中的任意一个数x,按照对应关系,在数集B中都有唯一
确定的数y和它对应。
函数的概念
三
设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数(function),记作:
y=f(x),x∈A
x叫做自变量,x的取值范围A叫做函数的定义域(domain);
与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}
叫做函数的值域(range)
函数的值域与集合B什么关系?请你说出上述四个问题的值域?
函数的值域是集合B的子集.
问题1和问题2中,值域就是集合B1和B2;
问题3和问题4中,值域是B3和B4的真子集.
思考
函数的概念的理解
四
(1) 定义域、值域、对应关系是函数的三个要素,不可分割,其中对 应关系有多种形式,如:解析式、图像、表格、Venn图、文字形式
如:y=ax+b可以写成f (x)= ax+b;当x=1时y=2可以写成f (1)=2
(2) y=f(x)为“y是x的函数”的数学表示,仅是一个函数符号,不能理解为y等于f与x的乘积
(3)y=f (x)是函数符号,可用任意字母表示,如:y=g(x),y=h(x);
函数的概念的理解
四
(5)f (a)与f (x)有什么区别?
一般地,f(a)表示当x=a时的函数值,是一个常量
f(x)表示自变量x的函数,一般情况下是变量
(4) 判断y=f(x),x∈A与u=f(v),v∈A的异同
函数相等,则定义域与对应关系相同
y=x与y=相同吗?
y=x与y=相同吗?
练一练
1.对于函数y=f (x),以下说法正确的有( )
①y是x的函数 ②对于不同的x,y的值也不同
③ f(a)表示当x=a时函数f(x)的值,是一个常量
④ f(x)一定可以用一个具体的式子表示出来
A.1个 B.2个 C.3个 D.4个
B
练一练
2.试确定一次函数、二次函数、反比例函数的定义域和值域
函 数 一次函数 二次函数 反比例函数
a>0 a<0
对应关系
定义域
值 域
x→ax+b
x→ ax2+bx+c
y=ax+b(a≠0)
y=ax2+bx+c (a≠0)
R
R
R
{x|x≠0}
R
{y|y≠0}
(k≠0)
练一练
例1. 函数的解析式是舍弃问题的实际背景而抽象出来的,它所反映的两个量之间的对应关系,可以广泛地用于刻画同一类事物中的变量关系和规律。例如,正比例函数y=kx(k≠0)可以用来刻画匀速运动中的路程与时间的关系、一定密度的物体的质量与体积的关系、圆的周长与半径的关系等。试构建一个问题情境,使其中的变量关系可以用解析式y=x(10-x)来描述。
解:长方形的周长为20,设一边长为x,面积为y,那么y=x(10-x).
其中,x的取值范围是A={x|0
课堂小结
五
1. 函数的定义
2. 函数相等的条件
设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数(function),记作:
y=f(x),x∈A
作业
教材P63 1,2,3,4
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
