数学人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程(共14张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 195.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-02 22:24:41 | ||
图片预览






文档简介
(共14张PPT)
3.2.1双曲线及其标准方程
差的绝对值
非零常数
小于
解读:
1,差的绝对值:
只有加上绝对值,才表示双曲线的两支
2,非零常数:如果等于零,则动点的轨迹是两焦点的垂直平分线
3,大于焦距时,动点轨迹不存在
等于焦距时,动点轨迹为以焦点为端点的射线
焦点
焦距
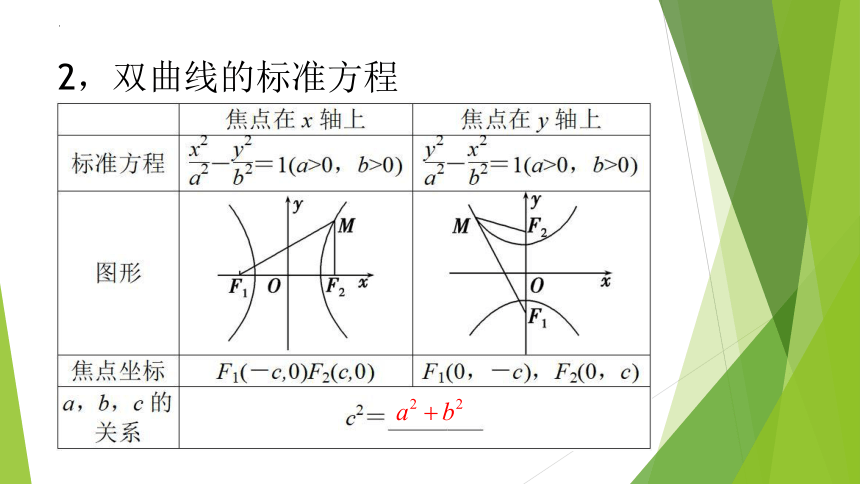
2,双曲线的标准方程
解读:
1,谁的系数是正的,焦点就在谁的轴上
即x的平方的系数为正,则焦点在x轴上
y的平方的系数为正,则焦点在y轴上
2,在椭圆中,a的值最大
在双曲线中,c的值最大
题型一:求双曲线的标准方程
总结:
求双曲线标准方程的方法:
1,定义法:由定义得到a,b的值,再确定焦点的位置,从而写出双曲线的方程
2,待定系数法:
(1)当焦点位置确定时,设出双曲线的标准方程,再代入点的坐标,从而求出方程;当焦点位置不确定时,可以把两种情况都设出来,再根据实际情况进行取舍
(2)当焦点位置不确定时,分情况讨论太复杂,所以可以设双曲线的方程为
题型二:求与双曲线有关的轨迹方程
总结:
求与双曲线有关的轨迹方程方法:
1,根据题意,列出等量关系
2,根据双曲线定义,找出所需量,从而写出方程
注意:
1,焦点所在的位置
2,自变量的取值范围
题型三:双曲线的实际应用
总结:
解决双曲线实际应用的方法:
1,在实际问题中找等量关系
2,利用等量关系得到几何关系
3,检验是否满足双曲线的定义,尤其要注意是双曲线的一支还是两支
课堂小结:
1,双曲线的定义
2,双曲线的标准方程
3,如何求双曲线的标准方程
4,如何求与双曲线有关的轨迹方程
5,如何解决双曲线的实际问题
课堂检测:
3.2.1双曲线及其标准方程
差的绝对值
非零常数
小于
解读:
1,差的绝对值:
只有加上绝对值,才表示双曲线的两支
2,非零常数:如果等于零,则动点的轨迹是两焦点的垂直平分线
3,大于焦距时,动点轨迹不存在
等于焦距时,动点轨迹为以焦点为端点的射线
焦点
焦距
2,双曲线的标准方程
解读:
1,谁的系数是正的,焦点就在谁的轴上
即x的平方的系数为正,则焦点在x轴上
y的平方的系数为正,则焦点在y轴上
2,在椭圆中,a的值最大
在双曲线中,c的值最大
题型一:求双曲线的标准方程
总结:
求双曲线标准方程的方法:
1,定义法:由定义得到a,b的值,再确定焦点的位置,从而写出双曲线的方程
2,待定系数法:
(1)当焦点位置确定时,设出双曲线的标准方程,再代入点的坐标,从而求出方程;当焦点位置不确定时,可以把两种情况都设出来,再根据实际情况进行取舍
(2)当焦点位置不确定时,分情况讨论太复杂,所以可以设双曲线的方程为
题型二:求与双曲线有关的轨迹方程
总结:
求与双曲线有关的轨迹方程方法:
1,根据题意,列出等量关系
2,根据双曲线定义,找出所需量,从而写出方程
注意:
1,焦点所在的位置
2,自变量的取值范围
题型三:双曲线的实际应用
总结:
解决双曲线实际应用的方法:
1,在实际问题中找等量关系
2,利用等量关系得到几何关系
3,检验是否满足双曲线的定义,尤其要注意是双曲线的一支还是两支
课堂小结:
1,双曲线的定义
2,双曲线的标准方程
3,如何求双曲线的标准方程
4,如何求与双曲线有关的轨迹方程
5,如何解决双曲线的实际问题
课堂检测:
