24.1.2垂直于弦的直径课件
文档属性
| 名称 | 24.1.2垂直于弦的直径课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 368.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-29 00:00:00 | ||
图片预览







文档简介
课件30张PPT。 24.1.2垂径定理 赵州桥坐落在河北省赵县洨河上。建于隋代(公元581-618年)大业年间(公元605-618年),由著名匠师李春设计和建造,距今已有约1400年的历史,是当今世界上现存最早、保存最完善的古代敞肩石拱桥。1961年被国务院列为第一批全国重点文物保护单位。因赵州桥是重点文物,通车易造成损坏,所以不允许车辆通行,但行人仍然可以自由通过。学习目标【知识与能力】 理解垂径定理并灵活运用垂径定理及圆的概念解决一些实际问题. 通过复合图形的折叠方法得出猜想垂径定理,并辅以逻辑证明加予理解.【过程与方法】【情感态度与价值观】 培养通过动手实践发现问题的能力.
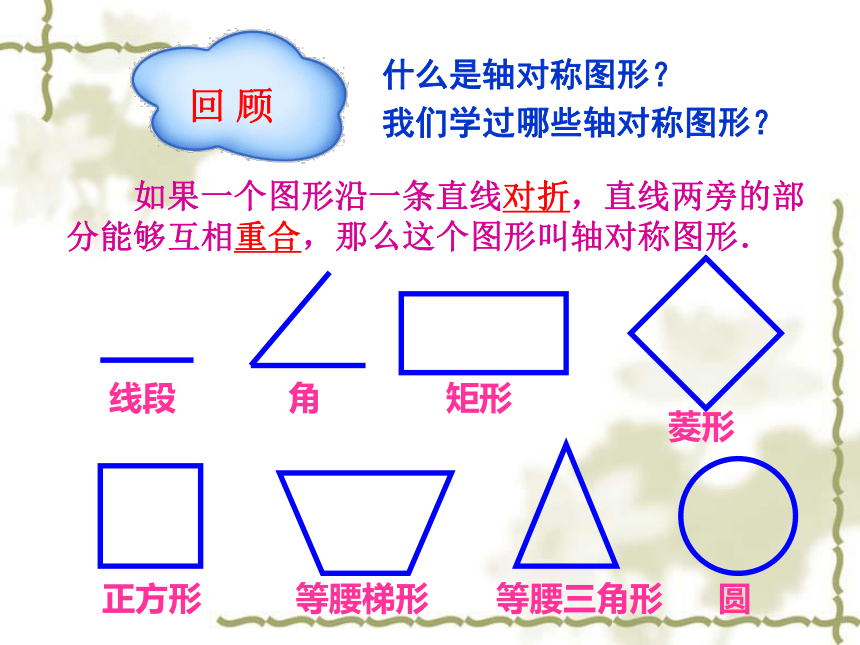
渗透“观察→分析→归纳→概括”的数学思想方法.学习重难点 垂径定理及其运用.什么是轴对称图形?
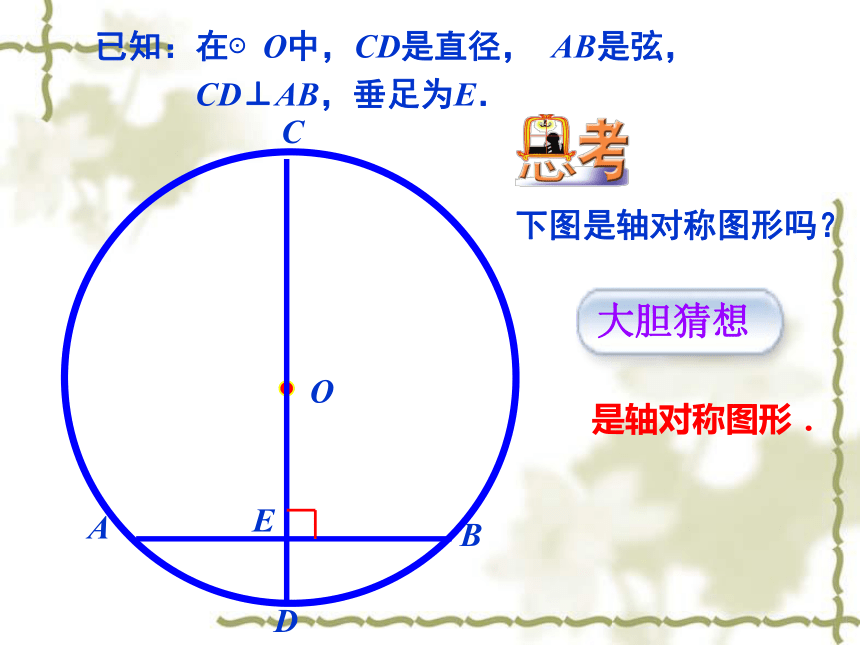
我们学过哪些轴对称图形? 如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形.回 顾线段角等腰三角形矩形菱形等腰梯形正方形圆任何一条直径所在的直线都是它的对称轴.圆有哪些对称轴?OOABCDE 是轴对称图形.大胆猜想已知:在⊙O中,CD是直径, AB是弦,
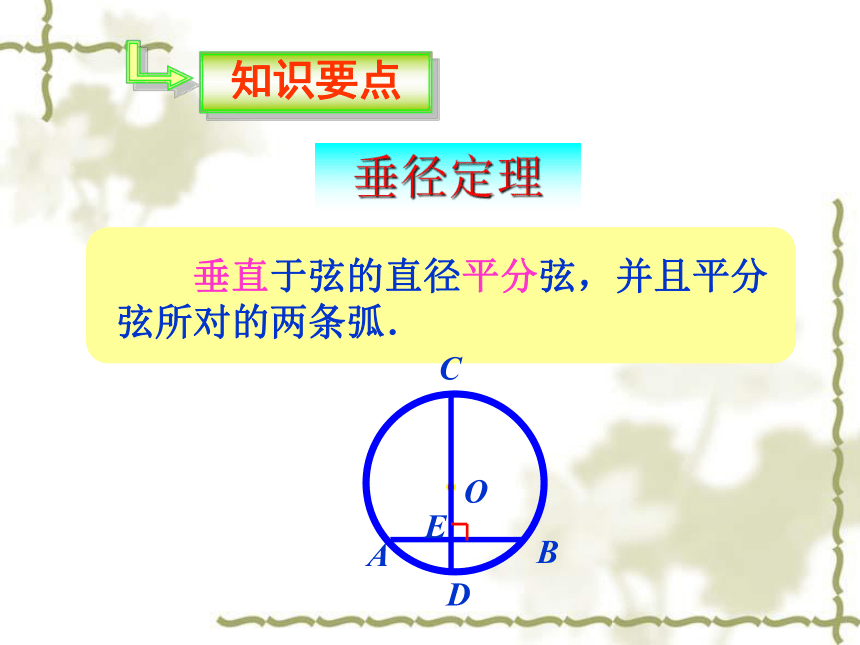
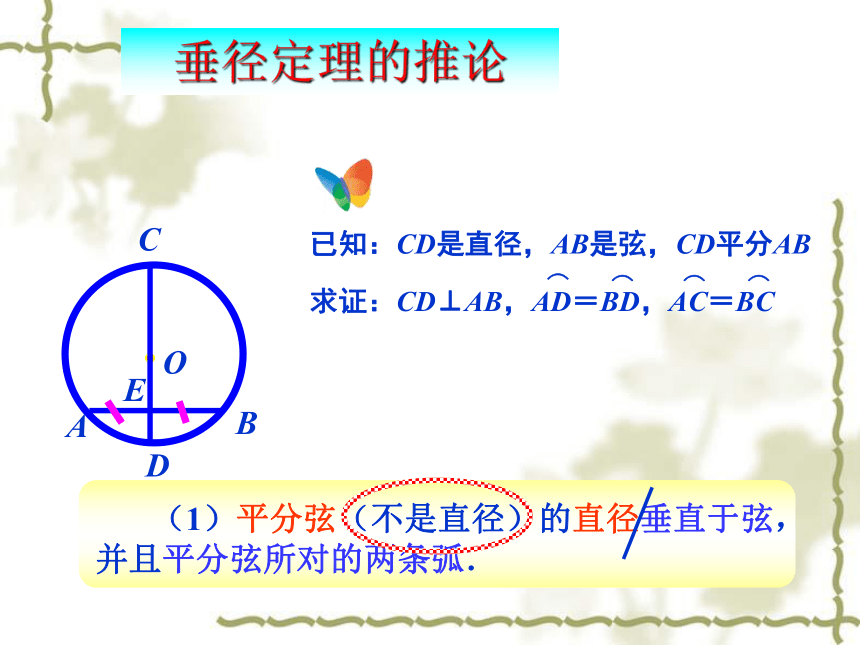
CD⊥AB,垂足为E. 下图是轴对称图形吗?叠合法 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 垂径定理CD是直径,AB是弦,
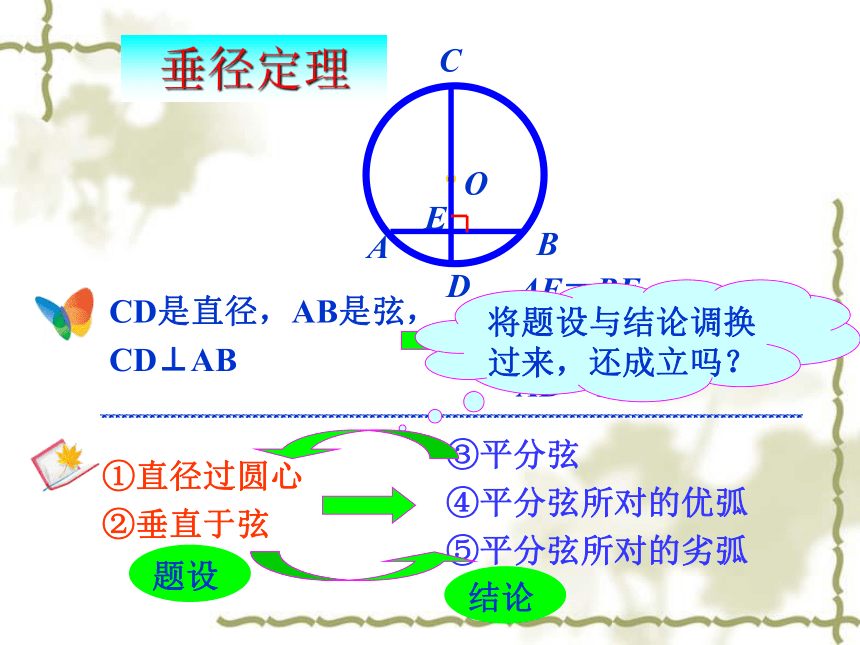
CD⊥AB①直径过圆心
②垂直于弦③平分弦
④平分弦所对的优弧
⑤平分弦所对的劣弧垂径定理将题设与结论调换过来,还成立吗? (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理的推论一个圆的任意两条直径总是互相平分,但它们不一定互相垂直.因此这里的弦如果是直径,结论不一定成立.OABMNCD注意为什么强调这里的弦不是直径?CDABE作法:1. 连结AB.小练习ABCDE作法:1. 连结AB.3. 连结AC.5. 点G同理.你能破镜重圆吗?ABCmnO 作弦AB、AC及它们的垂直平分线m、n,交于O点;以O为圆心,OA为半径作圆.作法:依据: 弦的垂直平分线经过圆心,并且平分弦所对的两条弧. 你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m. 赵州桥主桥拱的半径是多少? 垂径定理的应用 用 表示主桥拱,设 所在圆的圆心为O,半径为R.
经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是 的中点,CD 就是拱高.解:AB=37.4,CD=7.2,OD=OC-CD=R-7.2解得 R≈27.9(m)在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2课堂小结1. 圆是轴对称图形任何一条直径所在的直线都是它的对称轴. 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 2. 垂径定理 平分弦(不是直径)的直径垂直于弦并且平分弦所对的两条弧.3.垂径定理的推论4.将一条弧2等分和4等分的方法作弧所对着的弦的垂直平分线 经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.5. 解决有关弦的问题 1. 在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE解:答:⊙O的半径为5cm. 2. 在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,
求证:四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形. 3. 弓形的弦长为6cm,弓形的高为2cm,则这弓形所在的圆的半径为________. cm 4. 已知P为⊙O内一点,且OP=2cm,如果⊙O的半径是3cm,,那么过P点的最短的弦等于____________.cm5. 在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.
求证:AC=BD.证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE.
AE-CE=BE-DE.
所以,AC=BDE结论:在同圆或等圆中,平行弦所夹的弧相等。再见!
渗透“观察→分析→归纳→概括”的数学思想方法.学习重难点 垂径定理及其运用.什么是轴对称图形?
我们学过哪些轴对称图形? 如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形.回 顾线段角等腰三角形矩形菱形等腰梯形正方形圆任何一条直径所在的直线都是它的对称轴.圆有哪些对称轴?OOABCDE 是轴对称图形.大胆猜想已知:在⊙O中,CD是直径, AB是弦,
CD⊥AB,垂足为E. 下图是轴对称图形吗?叠合法 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 垂径定理CD是直径,AB是弦,
CD⊥AB①直径过圆心
②垂直于弦③平分弦
④平分弦所对的优弧
⑤平分弦所对的劣弧垂径定理将题设与结论调换过来,还成立吗? (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理的推论一个圆的任意两条直径总是互相平分,但它们不一定互相垂直.因此这里的弦如果是直径,结论不一定成立.OABMNCD注意为什么强调这里的弦不是直径?CDABE作法:1. 连结AB.小练习ABCDE作法:1. 连结AB.3. 连结AC.5. 点G同理.你能破镜重圆吗?ABCmnO 作弦AB、AC及它们的垂直平分线m、n,交于O点;以O为圆心,OA为半径作圆.作法:依据: 弦的垂直平分线经过圆心,并且平分弦所对的两条弧. 你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m. 赵州桥主桥拱的半径是多少? 垂径定理的应用 用 表示主桥拱,设 所在圆的圆心为O,半径为R.
经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是 的中点,CD 就是拱高.解:AB=37.4,CD=7.2,OD=OC-CD=R-7.2解得 R≈27.9(m)在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2课堂小结1. 圆是轴对称图形任何一条直径所在的直线都是它的对称轴. 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 2. 垂径定理 平分弦(不是直径)的直径垂直于弦并且平分弦所对的两条弧.3.垂径定理的推论4.将一条弧2等分和4等分的方法作弧所对着的弦的垂直平分线 经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.5. 解决有关弦的问题 1. 在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE解:答:⊙O的半径为5cm. 2. 在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,
求证:四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形. 3. 弓形的弦长为6cm,弓形的高为2cm,则这弓形所在的圆的半径为________. cm 4. 已知P为⊙O内一点,且OP=2cm,如果⊙O的半径是3cm,,那么过P点的最短的弦等于____________.cm5. 在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.
求证:AC=BD.证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE.
AE-CE=BE-DE.
所以,AC=BDE结论:在同圆或等圆中,平行弦所夹的弧相等。再见!
同课章节目录
