北师大版八年级数学上册第一章专题四模型拓展——勾股定理模型课件(共24张PPT)
文档属性
| 名称 | 北师大版八年级数学上册第一章专题四模型拓展——勾股定理模型课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 694.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 20:25:19 | ||
图片预览





文档简介
(共24张PPT)
专题四 模型拓展——勾股定理模型
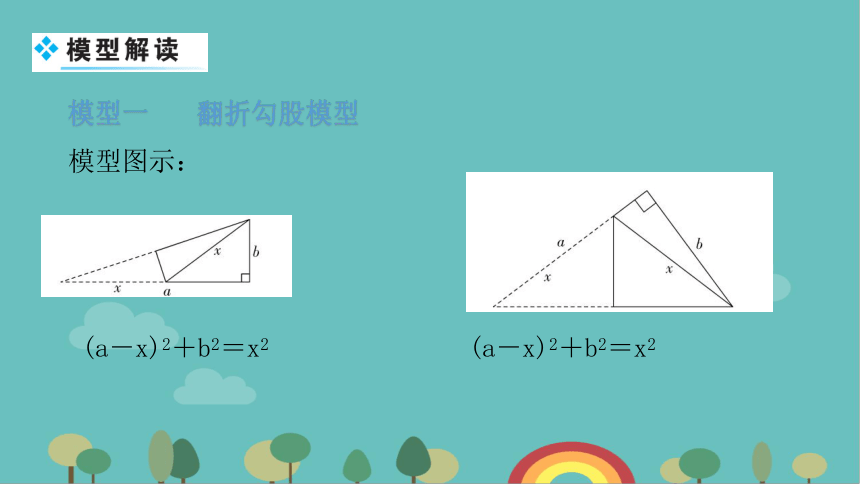
模型一 翻折勾股模型
模型图示:
(a-x)2+b2=x2 (a-x)2+b2=x2
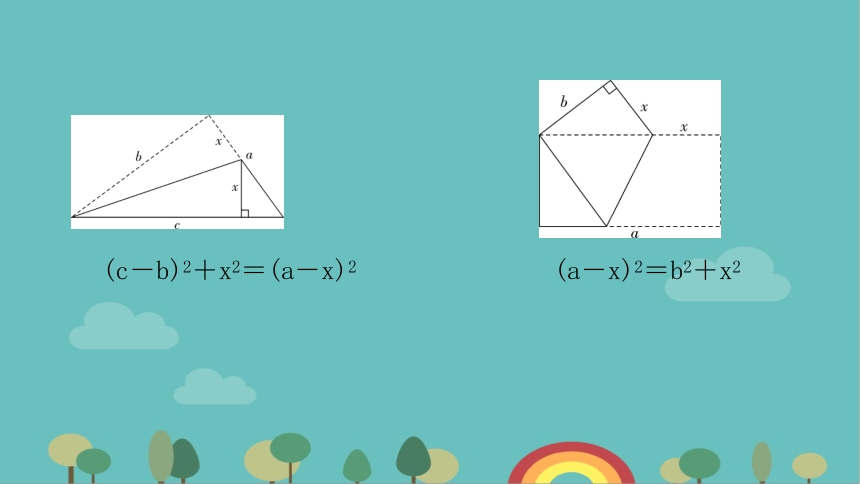
(c-b)2+x2=(a-x)2 (a-x)2=b2+x2
(a-x)2=b2+x2
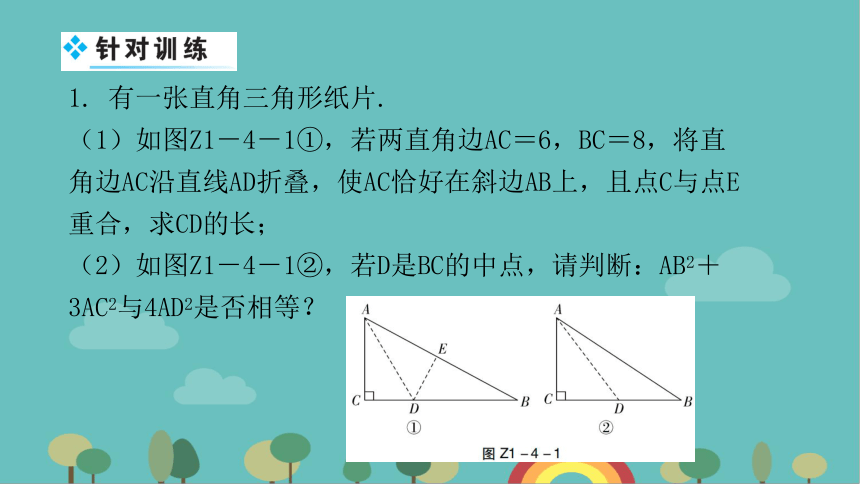
1. 有一张直角三角形纸片.
(1)如图Z1-4-1①,若两直角边AC=6,BC=8,将直角边AC沿直线AD折叠,使AC恰好在斜边AB上,且点C与点E重合,求CD的长;
(2)如图Z1-4-1②,若D是BC的中点,请判断:AB2+3AC2与4AD2是否相等?
(2)相等,理由如下:
在图Z1-4-1②中,
因为∠C=90°,
所以AB2=AC2+BC2,CD2=AD2-AC2.
因为D是BC的中点,
所以BC=2CD.
所以AB2=AC2+4CD2=AC2+4(AD2-AC2).
所以AB2=AC2+4AD2-4AC2.
所以AB2+3AC2=4AD2.
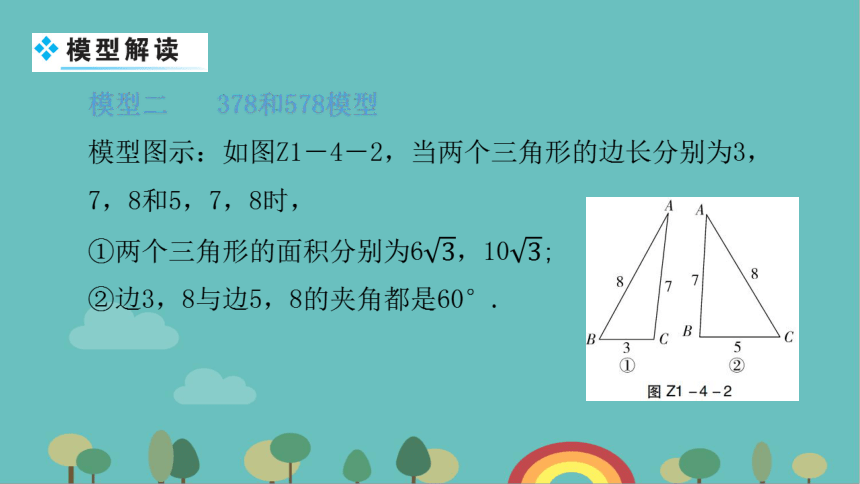
总结:如图Z1-4-2,观察这两个三角形,得这两个三角形的高相等,且有两边相等.如图Z1-4-3,将这个三角形拼在一起后构成一个边长为8的等边三角形,且该等边三角形的高即为这两个三角形的高.
2. 如图Z1-4-4,在△ABC中,AB=7,AC=8,BC=5,求∠C的度数.
解:如答图Z1-4-1,过点A作AD⊥BC于点D.
设CD=x,
则BD=BC-CD=5-x.
在Rt△ABD中,由勾股定理,
得AD2=AB2-BD2.
模型三 共边勾股模型
模型图示:
a2-b2=m2-n2=c2 a2-b2=m2-n2=c2
a2-b2=m2-n2=c2 a2-b2=m2+n2=c2
a2-b2=m2+n2=c2
3. 如图Z1-4-5,在△ABC中,AB=2,BC=6,AC=5,求边BC上的高.
模型四 等腰勾股模型
模型图示:
a2+b2=c2=(m+b)2 a2+b2=c2=(m-b)2
(m+a)2-a2=b2
4. 如图Z1-4-6,在△ABC中,AB=6,AC=8,BC=10,BC的垂直平分线分别交AC,BC于点D,E.求CD的长.
模型五 垂美模型
模型图示:
a2+d2=b2+c2
S四边形ABCD=(AC·BD)÷2
a2+d2=b2+c2
S四边形ABCD=(AC·BD)÷2
垂美四边形:对角线互相垂直的四边形.
垂美结论:垂美四边形对边的平方和相等.
5. 对角线互相垂直的四边形叫做垂美四边形.
(1)小美同学猜想“垂美四边形两组对边的平方和相等”,如图Z1-4-7①,在四边形ABCD中,若AC⊥BD,则AB2+CD2=AD2+BC2.请判断小美同学的猜想是否正确,并说明理由;
(2)如图Z1-4-7②.在△ABC中,BC=3,AC=4,D, E分别是AC, BC的中点,
连接AE, BD,且AE⊥BD,求AB.
解:(1)猜想正确,理由如下.
因为在四边形ABCD中,AC⊥BD,
所以∠AOB=∠COD=∠BOC=∠AOD=90°.
所以AB2=OA2+OB2,CD2=OC2+OD2,
BC2=OB2+OC2,AD2=OA2+OD2.
所以AB2+CD2=OA2+OB2+OC2+OD2,
BC2+AD2=OB2+OC2+OA2+OD2.
所以AB2+CD2=AD2+BC2.
谢 谢
专题四 模型拓展——勾股定理模型
模型一 翻折勾股模型
模型图示:
(a-x)2+b2=x2 (a-x)2+b2=x2
(c-b)2+x2=(a-x)2 (a-x)2=b2+x2
(a-x)2=b2+x2
1. 有一张直角三角形纸片.
(1)如图Z1-4-1①,若两直角边AC=6,BC=8,将直角边AC沿直线AD折叠,使AC恰好在斜边AB上,且点C与点E重合,求CD的长;
(2)如图Z1-4-1②,若D是BC的中点,请判断:AB2+3AC2与4AD2是否相等?
(2)相等,理由如下:
在图Z1-4-1②中,
因为∠C=90°,
所以AB2=AC2+BC2,CD2=AD2-AC2.
因为D是BC的中点,
所以BC=2CD.
所以AB2=AC2+4CD2=AC2+4(AD2-AC2).
所以AB2=AC2+4AD2-4AC2.
所以AB2+3AC2=4AD2.
总结:如图Z1-4-2,观察这两个三角形,得这两个三角形的高相等,且有两边相等.如图Z1-4-3,将这个三角形拼在一起后构成一个边长为8的等边三角形,且该等边三角形的高即为这两个三角形的高.
2. 如图Z1-4-4,在△ABC中,AB=7,AC=8,BC=5,求∠C的度数.
解:如答图Z1-4-1,过点A作AD⊥BC于点D.
设CD=x,
则BD=BC-CD=5-x.
在Rt△ABD中,由勾股定理,
得AD2=AB2-BD2.
模型三 共边勾股模型
模型图示:
a2-b2=m2-n2=c2 a2-b2=m2-n2=c2
a2-b2=m2-n2=c2 a2-b2=m2+n2=c2
a2-b2=m2+n2=c2
3. 如图Z1-4-5,在△ABC中,AB=2,BC=6,AC=5,求边BC上的高.
模型四 等腰勾股模型
模型图示:
a2+b2=c2=(m+b)2 a2+b2=c2=(m-b)2
(m+a)2-a2=b2
4. 如图Z1-4-6,在△ABC中,AB=6,AC=8,BC=10,BC的垂直平分线分别交AC,BC于点D,E.求CD的长.
模型五 垂美模型
模型图示:
a2+d2=b2+c2
S四边形ABCD=(AC·BD)÷2
a2+d2=b2+c2
S四边形ABCD=(AC·BD)÷2
垂美四边形:对角线互相垂直的四边形.
垂美结论:垂美四边形对边的平方和相等.
5. 对角线互相垂直的四边形叫做垂美四边形.
(1)小美同学猜想“垂美四边形两组对边的平方和相等”,如图Z1-4-7①,在四边形ABCD中,若AC⊥BD,则AB2+CD2=AD2+BC2.请判断小美同学的猜想是否正确,并说明理由;
(2)如图Z1-4-7②.在△ABC中,BC=3,AC=4,D, E分别是AC, BC的中点,
连接AE, BD,且AE⊥BD,求AB.
解:(1)猜想正确,理由如下.
因为在四边形ABCD中,AC⊥BD,
所以∠AOB=∠COD=∠BOC=∠AOD=90°.
所以AB2=OA2+OB2,CD2=OC2+OD2,
BC2=OB2+OC2,AD2=OA2+OD2.
所以AB2+CD2=OA2+OB2+OC2+OD2,
BC2+AD2=OB2+OC2+OA2+OD2.
所以AB2+CD2=AD2+BC2.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
