鲁教版(五四制)九年级上册2.5.1三角函数的应用课件(共16张PPT)
文档属性
| 名称 | 鲁教版(五四制)九年级上册2.5.1三角函数的应用课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 21:26:17 | ||
图片预览



文档简介
(共16张PPT)
三角函数的应用
(1)
直角三角形两锐角的关系:
直角三角形三边的关系:
回顾与思考
b
A
B
C
a
┌
c
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:
勾股定理 a +b =c .
两锐角互余 ∠A+∠B=90 .
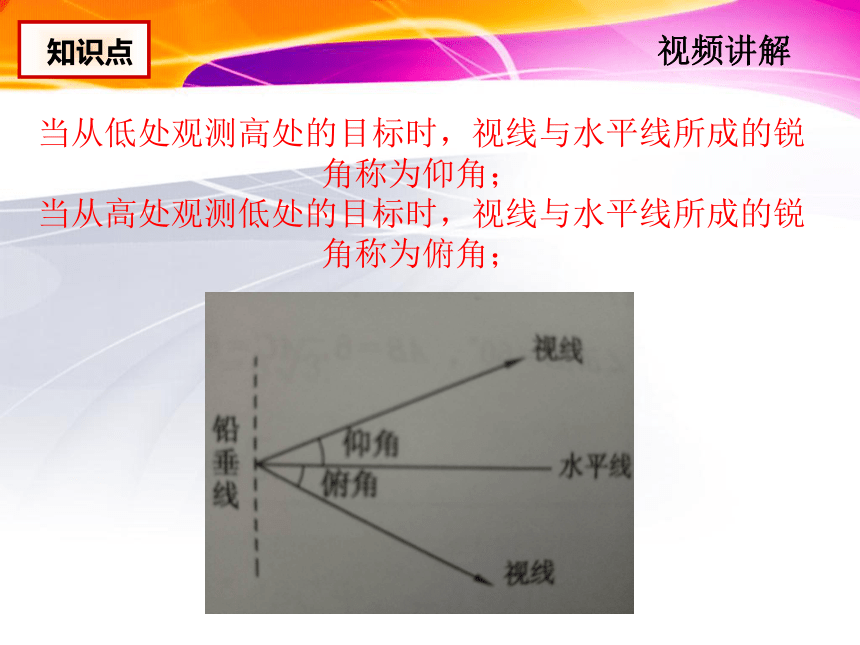
当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角;
当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角;
知识点
视频讲解
古塔究竟有多高
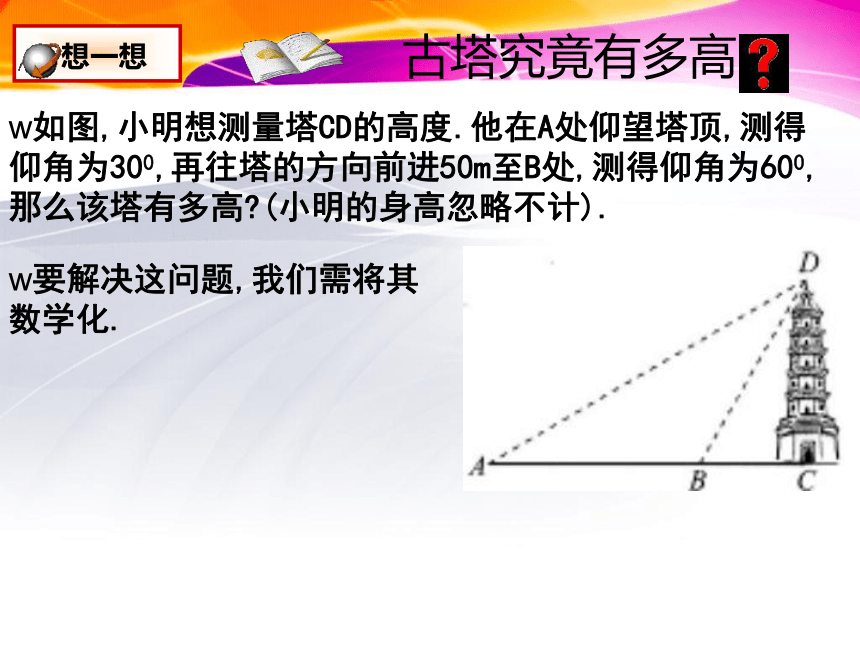
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高 (小明的身高忽略不计).
想一想
要解决这问题,我们需将其数学化.
解析
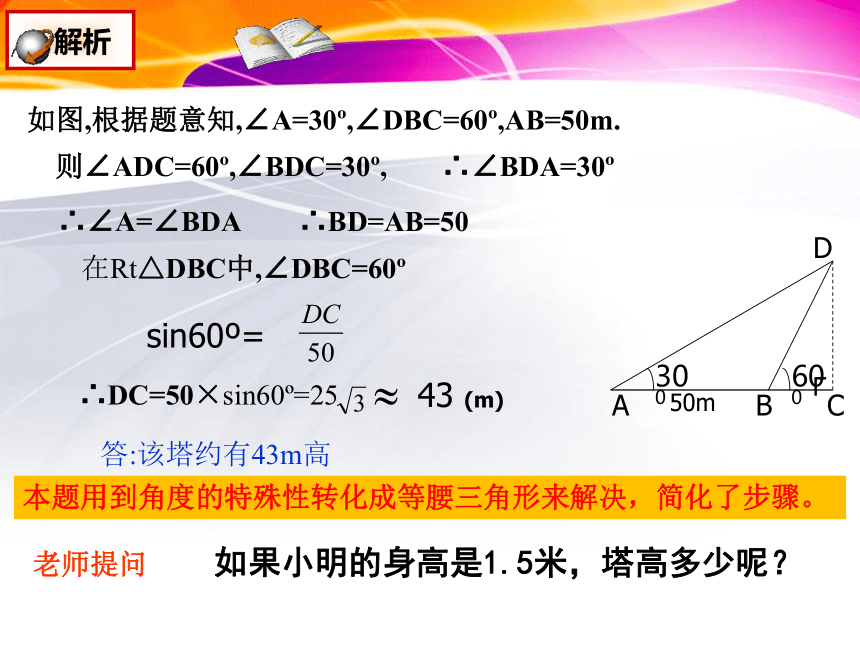
如图,根据题意知,∠A=30 ,∠DBC=60 ,AB=50m.
则∠ADC=60 ,∠BDC=30 ,
D
A
B
C
┌
50m
300
600
∴∠BDA=30
∴∠A=∠BDA
∴BD=AB=50
在Rt△DBC中,∠DBC=60
sin60 =
∴DC=50×sin60 =25
43
(m)
答:该塔约有43m高
老师提问
如果小明的身高是1.5米,塔高多少呢?
本题用到角度的特殊性转化成等腰三角形来解决,简化了步骤。
课堂小结:在运用锐角三角函数的知识解决实际问题时,你是如何思考的?
主要步骤:
1.分析实际问题中某些名词、概念的意义,正确理解条件和结论的关系;
2.将现实问题转化为数学问题,建立直角三角形模型;
3.根据条件特点,选用适当的锐角三角函数解决问题;
4、写出解答过程与答案 .
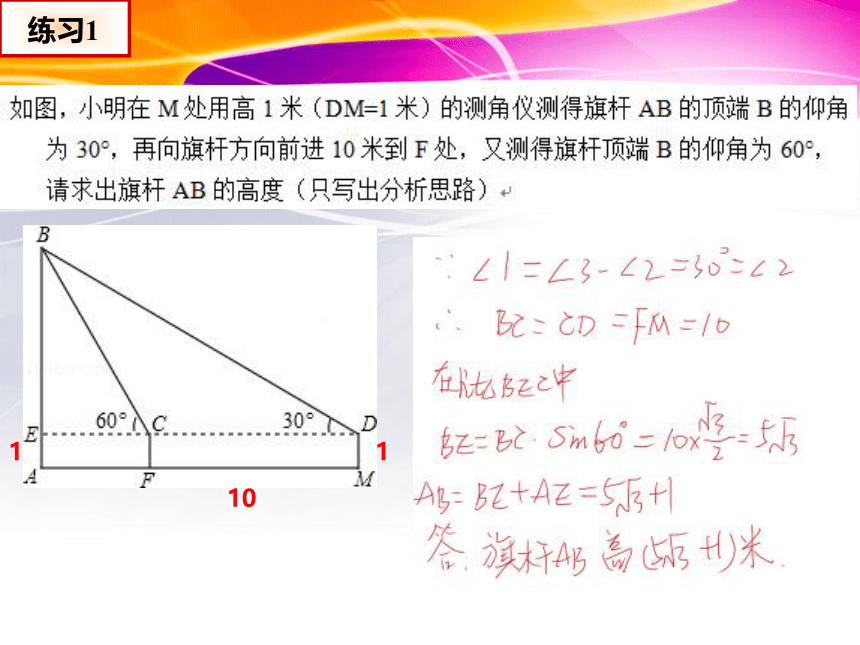
练习1
1
1
10
练习2
某商场准备改善原有楼梯的安全性能,把倾角由原来的450减至300,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面
A
B
C
D
┌
想一想
解:如图,根据题意可知,∠A=300,∠BDC=450,DB=4m.求(1)AB-BD的长,(2)AD的长.
A
B
C
D
┌
4m
300
450
答:调整后的楼梯会加长约 m.
解:如图,根据题意可知,∠A=300,∠BDC=450,DB=4m.求(2) AD的长.
A
B
C
D
┌
4m
300
450
答:楼梯多占约 一段地面.
解题过程
因为我们解决的都是两个有公共边的直角三角形,特对过程总结如下:
1、找边:找两直角三角形的公共边,
2、确定关系:确定公共边与已知边、与待求解边的关系,从而确定选择正弦、余弦还是正切,
3、熟练应用三角函数进行求解。
450
600
20
20
结束寄语
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.
下课了!
再见
三角函数的应用
(1)
直角三角形两锐角的关系:
直角三角形三边的关系:
回顾与思考
b
A
B
C
a
┌
c
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:
勾股定理 a +b =c .
两锐角互余 ∠A+∠B=90 .
当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角;
当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角;
知识点
视频讲解
古塔究竟有多高
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高 (小明的身高忽略不计).
想一想
要解决这问题,我们需将其数学化.
解析
如图,根据题意知,∠A=30 ,∠DBC=60 ,AB=50m.
则∠ADC=60 ,∠BDC=30 ,
D
A
B
C
┌
50m
300
600
∴∠BDA=30
∴∠A=∠BDA
∴BD=AB=50
在Rt△DBC中,∠DBC=60
sin60 =
∴DC=50×sin60 =25
43
(m)
答:该塔约有43m高
老师提问
如果小明的身高是1.5米,塔高多少呢?
本题用到角度的特殊性转化成等腰三角形来解决,简化了步骤。
课堂小结:在运用锐角三角函数的知识解决实际问题时,你是如何思考的?
主要步骤:
1.分析实际问题中某些名词、概念的意义,正确理解条件和结论的关系;
2.将现实问题转化为数学问题,建立直角三角形模型;
3.根据条件特点,选用适当的锐角三角函数解决问题;
4、写出解答过程与答案 .
练习1
1
1
10
练习2
某商场准备改善原有楼梯的安全性能,把倾角由原来的450减至300,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面
A
B
C
D
┌
想一想
解:如图,根据题意可知,∠A=300,∠BDC=450,DB=4m.求(1)AB-BD的长,(2)AD的长.
A
B
C
D
┌
4m
300
450
答:调整后的楼梯会加长约 m.
解:如图,根据题意可知,∠A=300,∠BDC=450,DB=4m.求(2) AD的长.
A
B
C
D
┌
4m
300
450
答:楼梯多占约 一段地面.
解题过程
因为我们解决的都是两个有公共边的直角三角形,特对过程总结如下:
1、找边:找两直角三角形的公共边,
2、确定关系:确定公共边与已知边、与待求解边的关系,从而确定选择正弦、余弦还是正切,
3、熟练应用三角函数进行求解。
450
600
20
20
结束寄语
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.
下课了!
再见
