鲁教版(五四制)九年级上册2.4解直角三角形课件(共18张PPT)
文档属性
| 名称 | 鲁教版(五四制)九年级上册2.4解直角三角形课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 21:29:20 | ||
图片预览



文档简介
(共18张PPT)
解直角三角形
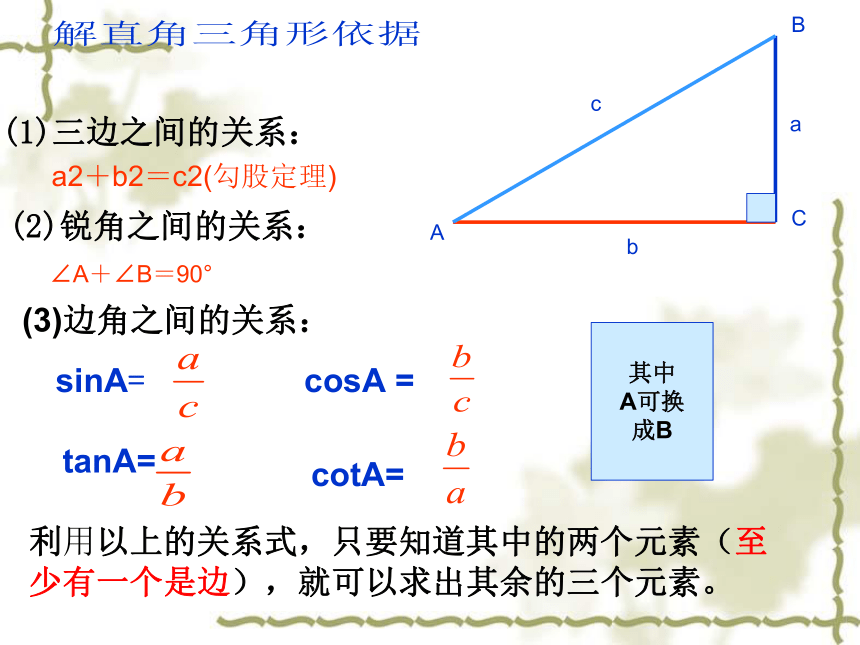
(1)三边之间的关系:
B
C
a
b
c
A
(2)锐角之间的关系:
a2+b2=c2(勾股定理)
∠A+∠B=90°
(3)边角之间的关系:
sinA=
cosA =
tanA=
cotA=
其中
A可换
成B
利用以上的关系式,只要知道其中的两个元素(至少有一个是边),就可以求出其余的三个元素。
解直角三角形依据
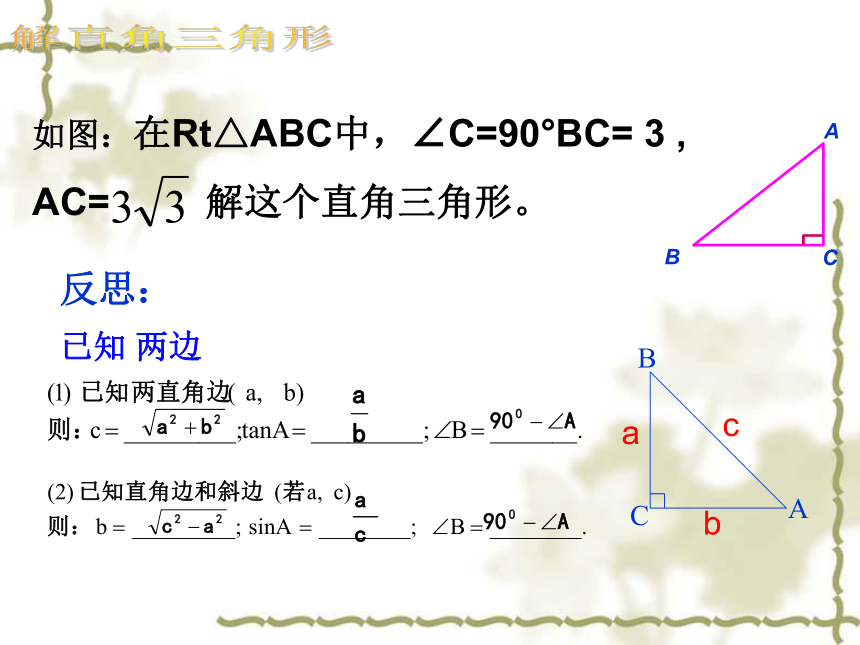
如图:在Rt△ABC中,∠C=90°BC= 3 ,
AC= 解这个直角三角形。
B
A
C
解直角三角形
已知 两边
反思:
A
B
C
a
c
b
1.已知两条边:
⑴两直角边
⑵一直角边和斜边
2.已知一边一角
猜想,解直角三角形的类型:
⑴一直角边和一锐角
⑵ 斜边和一锐角
例1:已知:在Rt△ABC中, ∠C=90°,∠A=60°,a=15,解这个直角
三角形.
C
B
A
b
a
c
解: ∵ ∠C=90°,∠A=60°
∴ ∠B=90°-∠A=30°
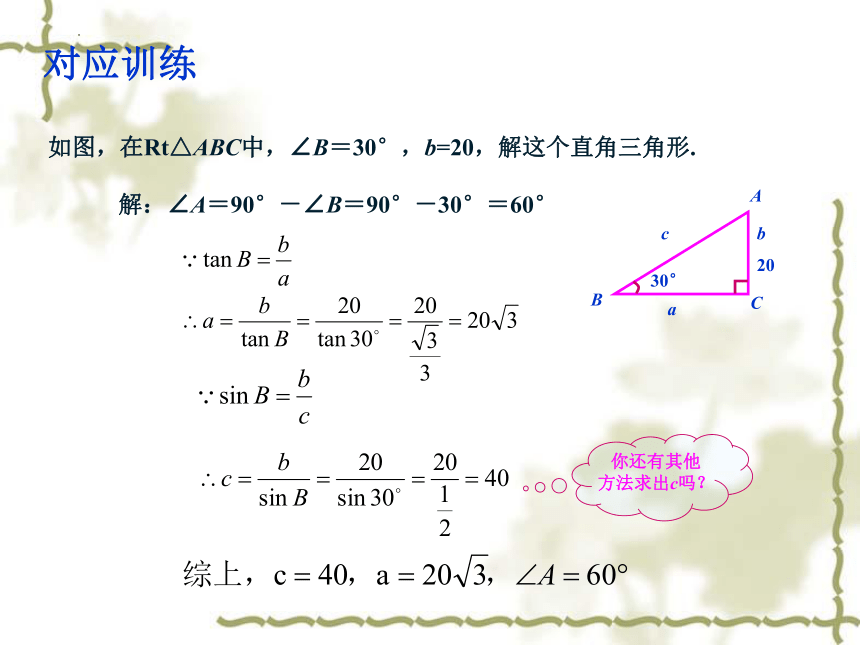
对应训练
如图,在Rt△ABC中,∠B=30°,b=20,解这个直角三角形.
解:∠A=90°-∠B=90°-30°=60°
A
B
C
a
b
c
20
30°
你还有其他方法求出c吗?
C
A
D
B
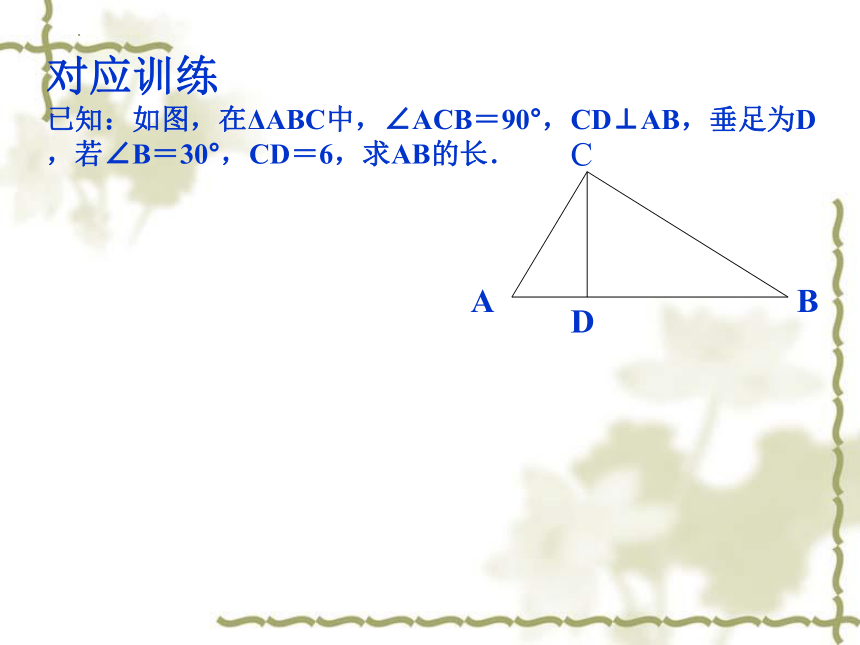
对应训练
已知:如图,在ΔABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
1、在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,求b, ∠A ,∠B
(2)已知b=10,∠B=60°,求 ∠A ,a,c.
(3)已知c=20,∠A=60°,求 ∠B, a,b.
(4)已知a=1,b= ,求c, ∠A, ∠B
尝试
在Rt△ABC中,∠C=90度,a,b,c分别是∠A,∠B,∠C的对边.
(1)已知 解这个直角三角形
(2)已知 解这个直角三角形
A
C
B
a
b
c
A
C
B
a
b
c
45°
30°
例2
对应训练
如图:Rt△ABC中,∠C=90°,∠A=30°,∠BDC=45°
求:(1)若BC=2,求AD
( 2 ) 若AD=4,求BC
小结
1、直角三角形解法
2、点睛:在求解直角三角形有关问题时, 要先画出图形以利于分析解决问题。
选择关系式时要尽量利用原始数据,以防止“累积误差”和“一错再错”
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边
D、已知两角
D
当堂练习
2.已知:在Rt△ABC中,∠C=90°,c= 8 ,∠A=60°,求∠B、a、b.
3.已知:在Rt△ABC中,∠C=90°,c=3 ,∠A=45°,求∠B、a、b.
A
B
C
如图,在△ABC中,已知AC=6,
∠ C=75°,∠B=45°,
求:AB的长;
⌒
75°
┓
D
⌒
450
⌒
60°
6
点睛:添加辅助线,“化斜为直”是我们常用的一种方法。
尝试中考
思考练习题
1、已知在△ABC中,∠C=90 ∠A=60 ,BC=5,BD是中线,则BD的长为_______
2、在△ABC中 ∠C=90 ,CD ⊥AB 于D
AD=4, sin ∠ACD= , CD=__BC=__
求b,c,tanB;
(2)a+C=12,b=8,求a,c,cosB
3、 △ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,
(1)a=4,,sinA=
小结
1、直角三角形解法
2、点睛:在求解直角三角形有关问题时, 要先画出图形以利于分析解决问题。
选择关系式时要尽量利用原始数据,以防止“累积误差”和“一错再错”
学习目标
互助合学
达标检测
师生答疑
配餐作业
知斜求直
知直求直
知边求角
正余弦
正余切
要选好
能用乘法不用除.
3、优选关系式
解直角三角形
(1)三边之间的关系:
B
C
a
b
c
A
(2)锐角之间的关系:
a2+b2=c2(勾股定理)
∠A+∠B=90°
(3)边角之间的关系:
sinA=
cosA =
tanA=
cotA=
其中
A可换
成B
利用以上的关系式,只要知道其中的两个元素(至少有一个是边),就可以求出其余的三个元素。
解直角三角形依据
如图:在Rt△ABC中,∠C=90°BC= 3 ,
AC= 解这个直角三角形。
B
A
C
解直角三角形
已知 两边
反思:
A
B
C
a
c
b
1.已知两条边:
⑴两直角边
⑵一直角边和斜边
2.已知一边一角
猜想,解直角三角形的类型:
⑴一直角边和一锐角
⑵ 斜边和一锐角
例1:已知:在Rt△ABC中, ∠C=90°,∠A=60°,a=15,解这个直角
三角形.
C
B
A
b
a
c
解: ∵ ∠C=90°,∠A=60°
∴ ∠B=90°-∠A=30°
对应训练
如图,在Rt△ABC中,∠B=30°,b=20,解这个直角三角形.
解:∠A=90°-∠B=90°-30°=60°
A
B
C
a
b
c
20
30°
你还有其他方法求出c吗?
C
A
D
B
对应训练
已知:如图,在ΔABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
1、在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,求b, ∠A ,∠B
(2)已知b=10,∠B=60°,求 ∠A ,a,c.
(3)已知c=20,∠A=60°,求 ∠B, a,b.
(4)已知a=1,b= ,求c, ∠A, ∠B
尝试
在Rt△ABC中,∠C=90度,a,b,c分别是∠A,∠B,∠C的对边.
(1)已知 解这个直角三角形
(2)已知 解这个直角三角形
A
C
B
a
b
c
A
C
B
a
b
c
45°
30°
例2
对应训练
如图:Rt△ABC中,∠C=90°,∠A=30°,∠BDC=45°
求:(1)若BC=2,求AD
( 2 ) 若AD=4,求BC
小结
1、直角三角形解法
2、点睛:在求解直角三角形有关问题时, 要先画出图形以利于分析解决问题。
选择关系式时要尽量利用原始数据,以防止“累积误差”和“一错再错”
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边
D、已知两角
D
当堂练习
2.已知:在Rt△ABC中,∠C=90°,c= 8 ,∠A=60°,求∠B、a、b.
3.已知:在Rt△ABC中,∠C=90°,c=3 ,∠A=45°,求∠B、a、b.
A
B
C
如图,在△ABC中,已知AC=6,
∠ C=75°,∠B=45°,
求:AB的长;
⌒
75°
┓
D
⌒
450
⌒
60°
6
点睛:添加辅助线,“化斜为直”是我们常用的一种方法。
尝试中考
思考练习题
1、已知在△ABC中,∠C=90 ∠A=60 ,BC=5,BD是中线,则BD的长为_______
2、在△ABC中 ∠C=90 ,CD ⊥AB 于D
AD=4, sin ∠ACD= , CD=__BC=__
求b,c,tanB;
(2)a+C=12,b=8,求a,c,cosB
3、 △ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,
(1)a=4,,sinA=
小结
1、直角三角形解法
2、点睛:在求解直角三角形有关问题时, 要先画出图形以利于分析解决问题。
选择关系式时要尽量利用原始数据,以防止“累积误差”和“一错再错”
学习目标
互助合学
达标检测
师生答疑
配餐作业
知斜求直
知直求直
知边求角
正余弦
正余切
要选好
能用乘法不用除.
3、优选关系式
