2022-2023学年度人教版数学八年级上册 第十二章全等三角形易错点例析课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年度人教版数学八年级上册 第十二章全等三角形易错点例析课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 641.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 17:24:26 | ||
图片预览







文档简介
(共20张PPT)
本章知识梳理
1.理解全等三角形的概念,能识别全等三角形中的对应边、对
应角.
2.掌握基本事实:两边及其夹角分别相等的两个三角形全等.
3.掌握基本事实:两角及其夹边分别相等的两个三角形全等.
课程标准
单元复习课
本章知识梳理
4.掌握基本事实:三边分别相等的两个三角形全等.
5.证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
6.探索并掌握判定直角三角形全等的“斜边、直角边”定理.
7.理解角平分线的概念,探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上.
全等形 能够完全重合的两个图形
全等三角形 概念:能够完全重合的两个三角形,表示符号为“≌”
性质:对应边相等;对应角相等;对应中线、角平分线和高相等;周长相等、面积相等
判定:1.边边边(SSS);2.边角边(SAS);3.角边角(ASA);4.角角边(AAS);5.HL(只适用于直角三角形)
角的平分线 性质:角的平分线上的点到角的两边的距离相等
判定:角的内部到角的两边的距离相等的点在角的平分线上
尺规作图 1.作一角等于已知角;2.作已知角的平分线
知识导航
第十二章 全等三角形
专题一 本章易错点例析
目录
01
易错典例
02
过关训练
易错点1.找错对应关系
易错典例
【例1】已知△ABC与△A′B′C′全等,且∠A=70°,∠B′=30°,∠A′=80°,BC=3,则A′B′的值为( )
A.3 B.4 C.5 D.不确定
错解:D.
错解分析:本题容易受惯性思维影响,把∠A的对应角看成∠A′,把∠B的对应角看成∠B′.本题根据已知条件,应该得到△ABC≌△C′A′B′或△ABC≌△C′B′A′,因此对应边相等,即A′B′=BC=3.
正解:A.
过关训练
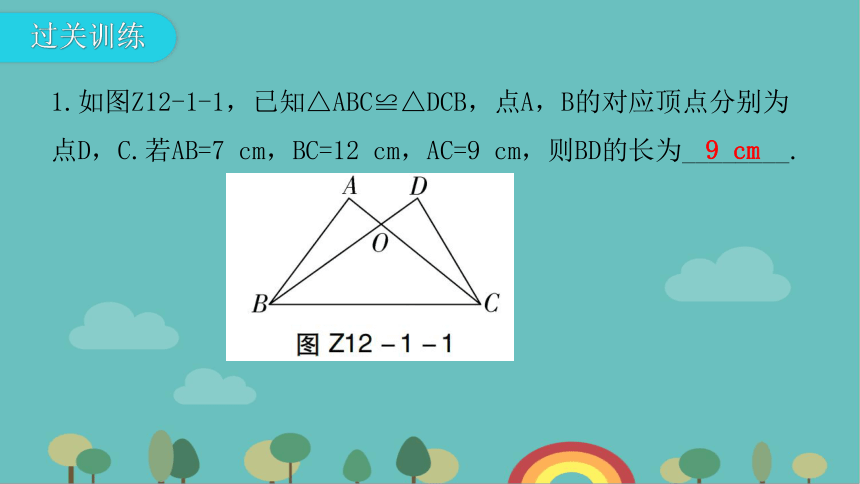
1.如图Z12-1-1,已知△ABC≌△DCB,点A,B的对应顶点分别为点D,C.若AB=7 cm,BC=12 cm,AC=9 cm,则BD的长为________.
9 cm
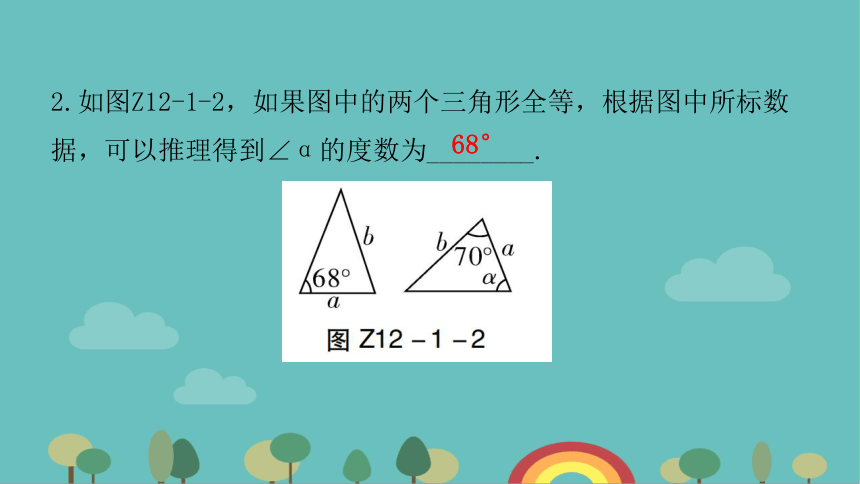
2.如图Z12-1-2,如果图中的两个三角形全等,根据图中所标数据,可以推理得到∠α的度数为________.
68°
易错点2.判定方法有错误
易错典例
过关训练
3.如图Z12-1-4,∠BAC=∠DAE=90°,∠B=∠C,AD=AE.求证:△ABD≌△ACE.
易错点3.错误套用等式性质
易错典例
过关训练
4.如图Z12-1-6,AB=AC,AD⊥BC.求证:BE=CE.
易错点4.把“AAA”或“SSA”当成判定三角形全等的条件来使用
易错典例
【例4】如图Z12-1-7, ∠CAB =∠DBA, ∠C=∠D, E为AC和BD的交点.△ADB与△BCA全等吗 请说明理由.
错解:△ADB ≌△BCA.
理由如下:
∵∠C = ∠D, ∠CAB = ∠DBA,
∴∠DAB =∠CBA.
∴△ADB ≌△BCA(AAA) .
过关训练
5.如图Z12-1-8,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.
谢 谢
本章知识梳理
1.理解全等三角形的概念,能识别全等三角形中的对应边、对
应角.
2.掌握基本事实:两边及其夹角分别相等的两个三角形全等.
3.掌握基本事实:两角及其夹边分别相等的两个三角形全等.
课程标准
单元复习课
本章知识梳理
4.掌握基本事实:三边分别相等的两个三角形全等.
5.证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
6.探索并掌握判定直角三角形全等的“斜边、直角边”定理.
7.理解角平分线的概念,探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上.
全等形 能够完全重合的两个图形
全等三角形 概念:能够完全重合的两个三角形,表示符号为“≌”
性质:对应边相等;对应角相等;对应中线、角平分线和高相等;周长相等、面积相等
判定:1.边边边(SSS);2.边角边(SAS);3.角边角(ASA);4.角角边(AAS);5.HL(只适用于直角三角形)
角的平分线 性质:角的平分线上的点到角的两边的距离相等
判定:角的内部到角的两边的距离相等的点在角的平分线上
尺规作图 1.作一角等于已知角;2.作已知角的平分线
知识导航
第十二章 全等三角形
专题一 本章易错点例析
目录
01
易错典例
02
过关训练
易错点1.找错对应关系
易错典例
【例1】已知△ABC与△A′B′C′全等,且∠A=70°,∠B′=30°,∠A′=80°,BC=3,则A′B′的值为( )
A.3 B.4 C.5 D.不确定
错解:D.
错解分析:本题容易受惯性思维影响,把∠A的对应角看成∠A′,把∠B的对应角看成∠B′.本题根据已知条件,应该得到△ABC≌△C′A′B′或△ABC≌△C′B′A′,因此对应边相等,即A′B′=BC=3.
正解:A.
过关训练
1.如图Z12-1-1,已知△ABC≌△DCB,点A,B的对应顶点分别为点D,C.若AB=7 cm,BC=12 cm,AC=9 cm,则BD的长为________.
9 cm
2.如图Z12-1-2,如果图中的两个三角形全等,根据图中所标数据,可以推理得到∠α的度数为________.
68°
易错点2.判定方法有错误
易错典例
过关训练
3.如图Z12-1-4,∠BAC=∠DAE=90°,∠B=∠C,AD=AE.求证:△ABD≌△ACE.
易错点3.错误套用等式性质
易错典例
过关训练
4.如图Z12-1-6,AB=AC,AD⊥BC.求证:BE=CE.
易错点4.把“AAA”或“SSA”当成判定三角形全等的条件来使用
易错典例
【例4】如图Z12-1-7, ∠CAB =∠DBA, ∠C=∠D, E为AC和BD的交点.△ADB与△BCA全等吗 请说明理由.
错解:△ADB ≌△BCA.
理由如下:
∵∠C = ∠D, ∠CAB = ∠DBA,
∴∠DAB =∠CBA.
∴△ADB ≌△BCA(AAA) .
过关训练
5.如图Z12-1-8,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.
谢 谢
