北师大版七年级数学上册字母表示数、代数式、整式一课一练(含答案)
文档属性
| 名称 | 北师大版七年级数学上册字母表示数、代数式、整式一课一练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 00:00:00 | ||
图片预览




文档简介
《字母表示数、代数式、整式》
一、单选题
1.下列式子表示不正确的是( )
A.m与5的积的平方记为 B.a与b的平方差是
C.比m除以n的商小5的数是 D.加上a等于b的数是
2.整式-0.3x2y,0,,-22abc2,x2, y, ab2-a2b中单项式的个数有( )
A.6个 B.5个 C.4个 D.3个
3.单项式的系数是( )
A.2 B.3 C.4 D.5
4.下列代数式属于二次三项式的是( )
A. B. C. D.
5.下列说法正确的是( )
①和都是单项式;②的项是x和1;③和都是多项式.
A.①② B.①③ C.②③ D.①②③
6.如图,阴影部分面积的表达式为( ).
A.ab-πa2 B.ab-πa2 C.ab-πa2 D.ab-πa2
7.某服装店新开张,第一天销售服装件,第二天比第一天多销售5件,第三天的销售量是第二天的3倍少9件,则第三天销售了( )
A.件 B.件
C.件 D.件
8.已知x﹣2y=4,xy=4,则代数式5xy﹣3x+6y的值为( )
A.32 B.16 C.8 D.﹣8
9.当时,代数式的值为2021,则当时,代数式的值为( )
A. B. C. D.2019
10.如图,用灰白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖块数为( )(用含n的代数式表示)
A.2+3n B.2n+3 C.3n-2 D.2n-3
11.下列说法中,正确的是( )
A.单项式xy2的系数是
B.单项式﹣6x2的次数为﹣6
C.多项式x3+2x+18是三次三项式
D.多项式3x2+y2﹣2的常数项是2
二、填空题
1.现有5元面值人民币m张,10元面值人民币n张,共有人民币________元(用含m、n的代数式表示).
2.方孔铜钱应天圆地方之说,古代人们认为天是圆的,地是方的.如图,现有一枚铜钱,图形外面是一个半径为r的圆,里面是一个边长为a的正方形,则阴影部分的面积是__________.(用的代数式表示)
3.小明买单价为x元的球拍a个,结账后还有27元,小明出门带了现金____元.
4.我校即将举办第22届阳光体育嘉年华,现计划新购进一批体育器材,其中实心球每个m元,拔河绳每根n元,则购进15个实心球,10根拔河绳共需______元.
5.单项式的系数是________,次数是_______.
6.多项式的次数是________.
7.多项式是____次____项式.
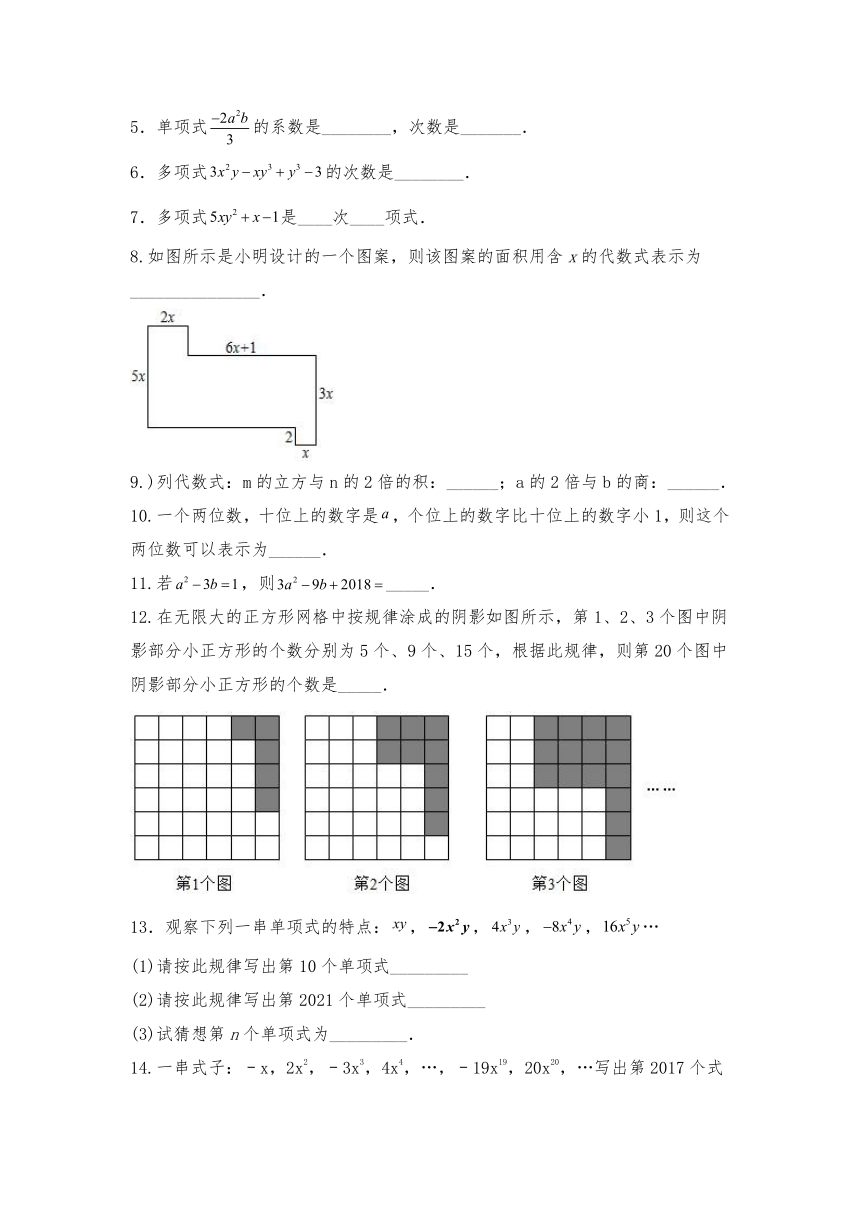
8.如图所示是小明设计的一个图案,则该图案的面积用含x的代数式表示为_______________.
9.)列代数式:m的立方与n的2倍的积:______;a的2倍与b的商:______.
10.一个两位数,十位上的数字是,个位上的数字比十位上的数字小1,则这个两位数可以表示为______.
11.若,则_____.
12.在无限大的正方形网格中按规律涂成的阴影如图所示,第1、2、3个图中阴影部分小正方形的个数分别为5个、9个、15个,根据此规律,则第20个图中阴影部分小正方形的个数是_____.
13.观察下列一串单项式的特点:,,,,…
(1)请按此规律写出第10个单项式_________
(2)请按此规律写出第2021个单项式_________
(3)试猜想第n个单项式为_________.
14.一串式子:﹣x,2x2,﹣3x3,4x4,…,﹣19x19,20x20,…写出第2017个式子_____,写出第n个______.
15.现在有4个小长方体纸盒,每个的长、宽、高都分别是a,b,c,a>2b且b>2c,若用这4个长方体纸盒搭成一个大长方体,搭成的大长方体的表面积最小为___________cm2,(用含a,b,c的代数式表示)
16.已知2m2+2mn﹣n2=3a﹣35,mn+2n2=2+a,则式子m2﹣mn﹣n2的值为__.
17.有一列式子,按一定规律排列成,,,,,…,第n个式子为_____(n为正整数)
三、解答题
1.某校在新建学生宿舍时需如图所示的铅合金窗框(别忘了中间还用了一根),它共用了长8米的铝合金,设长方形窗框的一边长为x米(如图).
(1)求长方形窗框的另一边长及窗框的面积(用含x的代数式表示).
(2)若x的取值分别为1,2,3,则哪一种取值所做的窗框面积最大?
2.指出下列各式中,哪些是单项式、哪些是多项式、哪些是整式?填在相应的横线上:①;②-x;③;④10;⑤6xy+1;⑥;⑦m2n;⑧2x2-x-5;⑨a7;⑩
单项式:____________________________;
多项式:________________________;
整式:________________________;
3.已知多项式x|m|﹣(m+2)x+12是关于x的二次二项式,求m的值.
4.如图, 在宽为米,长为米的长方形地面上,修筑宽度为米的两条互相垂直的小路,余下的部分作为草地,现给两条小路铺上地砖,选用地砖的价格是每平米元.
(1)买地砖需要多少元 (用含的式子表示);
(2)当时,计算地砖的费用.
5.某房间窗户如图所示.其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同).
(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光的部分的面积是多少?
6.已知a,b,c,d,x,y均为有理数,按要求解答下列问题:
(1)已知a,b互为相反数,c,d互为倒数,则a+b= ,cd= ;
(2)在(1)的条件下,若x,y满足|x+|+|y﹣|=0,求﹣2(a+b)﹣cd+x﹣y的值.
7.小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同).
(1)请用代数式表示装饰物的面积:______;
用代数式表示窗户能射进阳光的面积:______;(结果保留)
(2)小亮又设计了如图2的空帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(用代数式表示)
8.观察下列一组单项式:,,,,….
(1)直接写出第5个单项式为____,第6个单项式_____;
(2)直接写出第个单项式(为正整数);
(3)是否存在某一项的系数为的情况?如果存在,求出这是第几项;如果不存在,请说明理由.
答案
一、单选题
A. B. C.C.B.D.A.C.C.A.C.
二、填空题
1.
2.πr2-a2.
3.(ax+27).
4.(15m+10n).
5.,3.
6.4.
7.三,三.
8.
9.;.
10.11a-1.
11.2021.
12.423
13.-512x10y,-22020x2021y,(-1)n+12n-1xny.
14.-2017x2017;(-1)nnxn.
15.4ab+4ac+8bc.
16.
17..
三、解答题
1.解:(1)由题意得,另一边长:,面积为:x(8-2x);
(2)当x=1,面积为x(8-2x)=2;
当x=2,面积为x(8-2x)=;
当x=3,面积为x(8-2x)=2,
故当x=2时,面积最大.
2.解:单项式有:-x,10,m2n,a7;
多项式有:,,6xy+1,2x2-x-5;
整式有:,-x,,10,6xy+1,m2n,2x2-x-5,a7.
3.解:∵多项式x|m|﹣(m+2)x+12是关于x的二次二项式,
∴|m|=2,且m+2=0,
∴m=﹣2.
即m的值是﹣2.
4.解:依题意, 地砖的面积为,
所以买地砖至少需要元
当时,
.
所以当时,地砖的费用是元.
5.(1)装饰物的面积正好等于一个半径为的圆的面积=;
(2)窗户中能射进阳光的部分的面积是.
6.解:(1)∵a,b互为相反数,c,d互为倒数,
∴a+b=0,cd=1;
故答案为:0、1.
(2)∵x,y满足|x+|+|y﹣|=0,
∴x+=0,y﹣=0,
解得x=﹣,y=,
∴﹣2(a+b)﹣cd+x﹣y
=﹣2×0﹣1+(﹣)﹣
=0﹣1﹣1
=﹣2.
7.(1)由题意知:四分之一圆的半径为,
∴装饰物的面积为==,
∴窗户能射进阳光的面积为=ab-,
故答案为:,ab-;
(2)图2窗户能射进阳光的面积= ,
∵>,
∴ab-< ,
∴此时,窗户能射进阳光的面积更大,
()-(ab-)=-ab+=,
∴此时,窗户能射进阳光的面积比原来大
8.解:(1)第1个单项式=;
第2个单项式=;
第3个单项式=;
第4个单项式=;
∴第5个单项式为=;
第6个单项式为=;
故答案为:;;
(2)由(1)得,第个单项式为;
(3)可能
∵
∴当时,其系数为
∴第20个单项式的系数为.
一、单选题
1.下列式子表示不正确的是( )
A.m与5的积的平方记为 B.a与b的平方差是
C.比m除以n的商小5的数是 D.加上a等于b的数是
2.整式-0.3x2y,0,,-22abc2,x2, y, ab2-a2b中单项式的个数有( )
A.6个 B.5个 C.4个 D.3个
3.单项式的系数是( )
A.2 B.3 C.4 D.5
4.下列代数式属于二次三项式的是( )
A. B. C. D.
5.下列说法正确的是( )
①和都是单项式;②的项是x和1;③和都是多项式.
A.①② B.①③ C.②③ D.①②③
6.如图,阴影部分面积的表达式为( ).
A.ab-πa2 B.ab-πa2 C.ab-πa2 D.ab-πa2
7.某服装店新开张,第一天销售服装件,第二天比第一天多销售5件,第三天的销售量是第二天的3倍少9件,则第三天销售了( )
A.件 B.件
C.件 D.件
8.已知x﹣2y=4,xy=4,则代数式5xy﹣3x+6y的值为( )
A.32 B.16 C.8 D.﹣8
9.当时,代数式的值为2021,则当时,代数式的值为( )
A. B. C. D.2019
10.如图,用灰白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖块数为( )(用含n的代数式表示)
A.2+3n B.2n+3 C.3n-2 D.2n-3
11.下列说法中,正确的是( )
A.单项式xy2的系数是
B.单项式﹣6x2的次数为﹣6
C.多项式x3+2x+18是三次三项式
D.多项式3x2+y2﹣2的常数项是2
二、填空题
1.现有5元面值人民币m张,10元面值人民币n张,共有人民币________元(用含m、n的代数式表示).
2.方孔铜钱应天圆地方之说,古代人们认为天是圆的,地是方的.如图,现有一枚铜钱,图形外面是一个半径为r的圆,里面是一个边长为a的正方形,则阴影部分的面积是__________.(用的代数式表示)
3.小明买单价为x元的球拍a个,结账后还有27元,小明出门带了现金____元.
4.我校即将举办第22届阳光体育嘉年华,现计划新购进一批体育器材,其中实心球每个m元,拔河绳每根n元,则购进15个实心球,10根拔河绳共需______元.
5.单项式的系数是________,次数是_______.
6.多项式的次数是________.
7.多项式是____次____项式.
8.如图所示是小明设计的一个图案,则该图案的面积用含x的代数式表示为_______________.
9.)列代数式:m的立方与n的2倍的积:______;a的2倍与b的商:______.
10.一个两位数,十位上的数字是,个位上的数字比十位上的数字小1,则这个两位数可以表示为______.
11.若,则_____.
12.在无限大的正方形网格中按规律涂成的阴影如图所示,第1、2、3个图中阴影部分小正方形的个数分别为5个、9个、15个,根据此规律,则第20个图中阴影部分小正方形的个数是_____.
13.观察下列一串单项式的特点:,,,,…
(1)请按此规律写出第10个单项式_________
(2)请按此规律写出第2021个单项式_________
(3)试猜想第n个单项式为_________.
14.一串式子:﹣x,2x2,﹣3x3,4x4,…,﹣19x19,20x20,…写出第2017个式子_____,写出第n个______.
15.现在有4个小长方体纸盒,每个的长、宽、高都分别是a,b,c,a>2b且b>2c,若用这4个长方体纸盒搭成一个大长方体,搭成的大长方体的表面积最小为___________cm2,(用含a,b,c的代数式表示)
16.已知2m2+2mn﹣n2=3a﹣35,mn+2n2=2+a,则式子m2﹣mn﹣n2的值为__.
17.有一列式子,按一定规律排列成,,,,,…,第n个式子为_____(n为正整数)
三、解答题
1.某校在新建学生宿舍时需如图所示的铅合金窗框(别忘了中间还用了一根),它共用了长8米的铝合金,设长方形窗框的一边长为x米(如图).
(1)求长方形窗框的另一边长及窗框的面积(用含x的代数式表示).
(2)若x的取值分别为1,2,3,则哪一种取值所做的窗框面积最大?
2.指出下列各式中,哪些是单项式、哪些是多项式、哪些是整式?填在相应的横线上:①;②-x;③;④10;⑤6xy+1;⑥;⑦m2n;⑧2x2-x-5;⑨a7;⑩
单项式:____________________________;
多项式:________________________;
整式:________________________;
3.已知多项式x|m|﹣(m+2)x+12是关于x的二次二项式,求m的值.
4.如图, 在宽为米,长为米的长方形地面上,修筑宽度为米的两条互相垂直的小路,余下的部分作为草地,现给两条小路铺上地砖,选用地砖的价格是每平米元.
(1)买地砖需要多少元 (用含的式子表示);
(2)当时,计算地砖的费用.
5.某房间窗户如图所示.其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同).
(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光的部分的面积是多少?
6.已知a,b,c,d,x,y均为有理数,按要求解答下列问题:
(1)已知a,b互为相反数,c,d互为倒数,则a+b= ,cd= ;
(2)在(1)的条件下,若x,y满足|x+|+|y﹣|=0,求﹣2(a+b)﹣cd+x﹣y的值.
7.小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同).
(1)请用代数式表示装饰物的面积:______;
用代数式表示窗户能射进阳光的面积:______;(结果保留)
(2)小亮又设计了如图2的空帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(用代数式表示)
8.观察下列一组单项式:,,,,….
(1)直接写出第5个单项式为____,第6个单项式_____;
(2)直接写出第个单项式(为正整数);
(3)是否存在某一项的系数为的情况?如果存在,求出这是第几项;如果不存在,请说明理由.
答案
一、单选题
A. B. C.C.B.D.A.C.C.A.C.
二、填空题
1.
2.πr2-a2.
3.(ax+27).
4.(15m+10n).
5.,3.
6.4.
7.三,三.
8.
9.;.
10.11a-1.
11.2021.
12.423
13.-512x10y,-22020x2021y,(-1)n+12n-1xny.
14.-2017x2017;(-1)nnxn.
15.4ab+4ac+8bc.
16.
17..
三、解答题
1.解:(1)由题意得,另一边长:,面积为:x(8-2x);
(2)当x=1,面积为x(8-2x)=2;
当x=2,面积为x(8-2x)=;
当x=3,面积为x(8-2x)=2,
故当x=2时,面积最大.
2.解:单项式有:-x,10,m2n,a7;
多项式有:,,6xy+1,2x2-x-5;
整式有:,-x,,10,6xy+1,m2n,2x2-x-5,a7.
3.解:∵多项式x|m|﹣(m+2)x+12是关于x的二次二项式,
∴|m|=2,且m+2=0,
∴m=﹣2.
即m的值是﹣2.
4.解:依题意, 地砖的面积为,
所以买地砖至少需要元
当时,
.
所以当时,地砖的费用是元.
5.(1)装饰物的面积正好等于一个半径为的圆的面积=;
(2)窗户中能射进阳光的部分的面积是.
6.解:(1)∵a,b互为相反数,c,d互为倒数,
∴a+b=0,cd=1;
故答案为:0、1.
(2)∵x,y满足|x+|+|y﹣|=0,
∴x+=0,y﹣=0,
解得x=﹣,y=,
∴﹣2(a+b)﹣cd+x﹣y
=﹣2×0﹣1+(﹣)﹣
=0﹣1﹣1
=﹣2.
7.(1)由题意知:四分之一圆的半径为,
∴装饰物的面积为==,
∴窗户能射进阳光的面积为=ab-,
故答案为:,ab-;
(2)图2窗户能射进阳光的面积= ,
∵>,
∴ab-< ,
∴此时,窗户能射进阳光的面积更大,
()-(ab-)=-ab+=,
∴此时,窗户能射进阳光的面积比原来大
8.解:(1)第1个单项式=;
第2个单项式=;
第3个单项式=;
第4个单项式=;
∴第5个单项式为=;
第6个单项式为=;
故答案为:;;
(2)由(1)得,第个单项式为;
(3)可能
∵
∴当时,其系数为
∴第20个单项式的系数为.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
