数学人教A版(2019)必修第一册3.2.2函数的奇偶性(共40张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.2.2函数的奇偶性(共40张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 837.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 11:42:07 | ||
图片预览







文档简介
(共40张PPT)
(第一册) 第三章 函数的概念与性质
函数的基本性质
函数的奇偶性(第一课时)
2022年10月3日星期一
1
人教A版(2019)必修第一册
【学习目标】
奇函数的概念;
偶函数的概念;
函数奇偶性的判断;
【学习重点】
函数奇偶性的概念
【学习难点】
函数奇偶性的判断
【自学指导】阅读课本P82-84思考下列问题
1、奇函数与偶函数的概念分别是什么?
2、奇函数与偶函数的图像分别有什么特征?
3、判断函数的奇偶性的步骤是什么?
引入
引 例
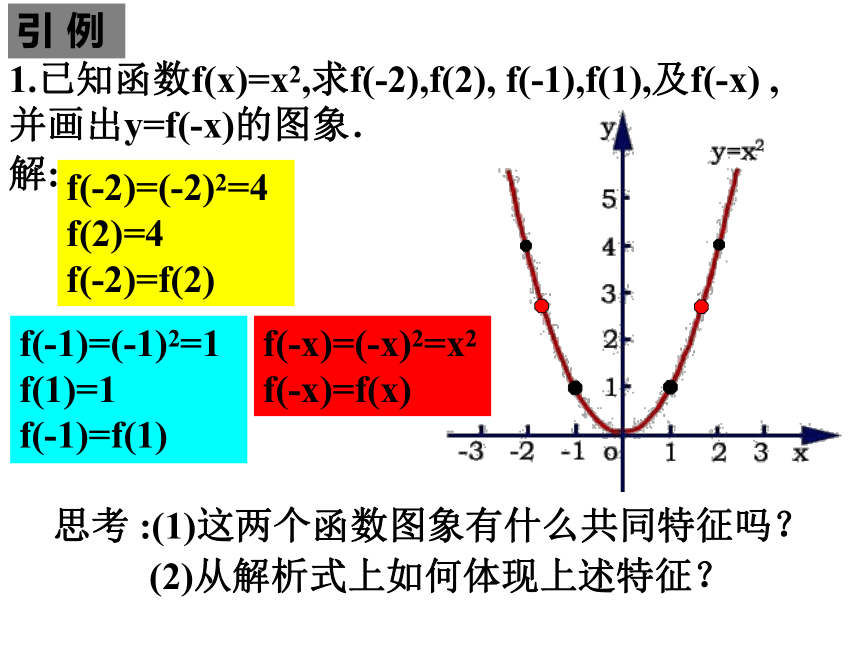
1.已知函数f(x)=x2,求f(-2),f(2), f(-1),f(1),及f(-x) ,并画出y=f(-x)的图象.
解:
f(-2)=(-2)2=4 f(2)=4
f(-2)=f(2)
f(-1)=(-1)2=1 f(1)=1
f(-1)=f(1)
f(-x)=(-x)2=x2
f(-x)=f(x)
思考 :(1)这两个函数图象有什么共同特征吗?
(2)从解析式上如何体现上述特征?
偶函数的特征:
①解析式的基本特征:
f (-x)=f (x)
②图像特征:关于y轴对称.
如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数。
1. 偶函数的概念
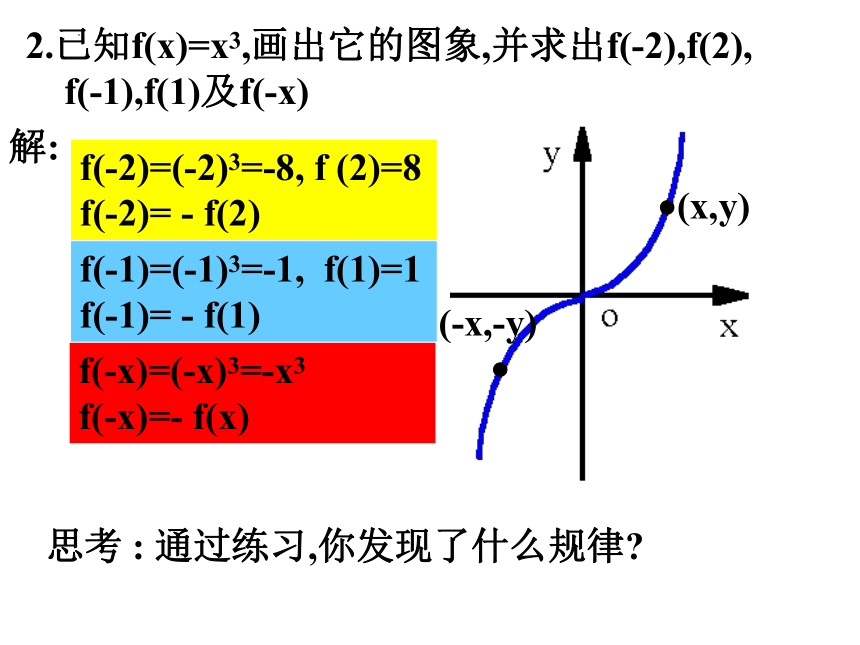
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),
f(-1),f(1)及f(-x)
解:
f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)
f(-1)=(-1)3=-1, f(1)=1 f(-1)= - f(1)
f(-x)=(-x)3=-x3 f(-x)=- f(x)
思考 : 通过练习,你发现了什么规律
(-x,-y)
(x,y)
奇函数的特征:
①解析式的基本特征:
f (-x)=-f (x)
②图像特征:关于原点对称.
如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数。
2.奇函数的概念
如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.
3.奇偶性的概念
(1)若f(x)为奇函数, 则f(-x)=-f(x)成立.
若f(x)为偶函数, 则f(-x)= f(x) 成立.
(2)判断函数是否具有奇偶性.首先要看函数的定义域是否关于原点对称,即函数定义域关于原点对称是函数具有奇偶性的前提.
注意事项
[a ,b]
[-b,-a]
x
o
(3)函数的奇偶性是函数的整体性质;而函数的单调性是函数的局部性质.
奇函数的图象(如y=x3 )
偶函数的图象(如y=x2)
y
x
o
a
a
P/(-a ,f(-a))
p(a ,f(a))
-a
y
x
o
a
P/(-a ,f(-a))
p(a ,f(a))
-a
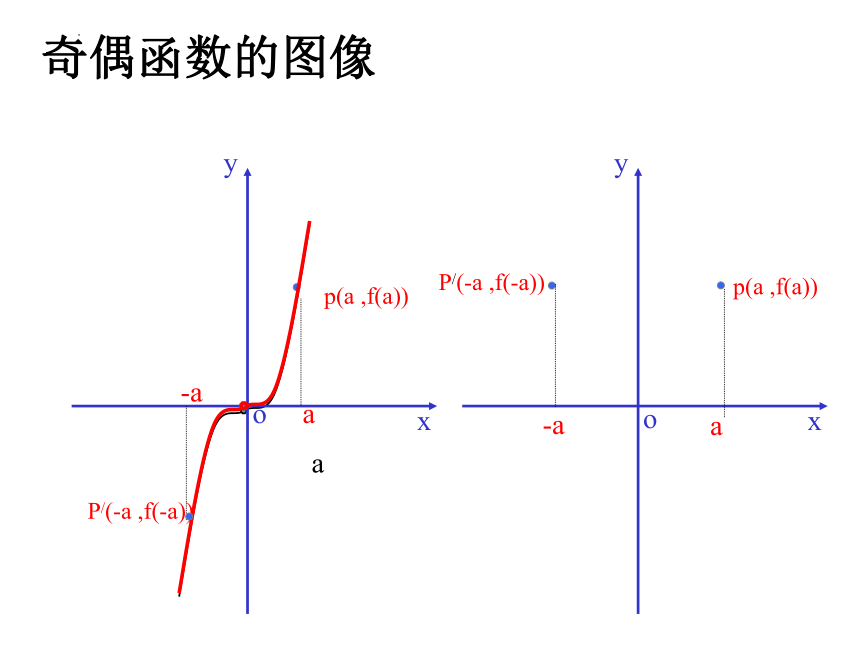
奇偶函数的图像
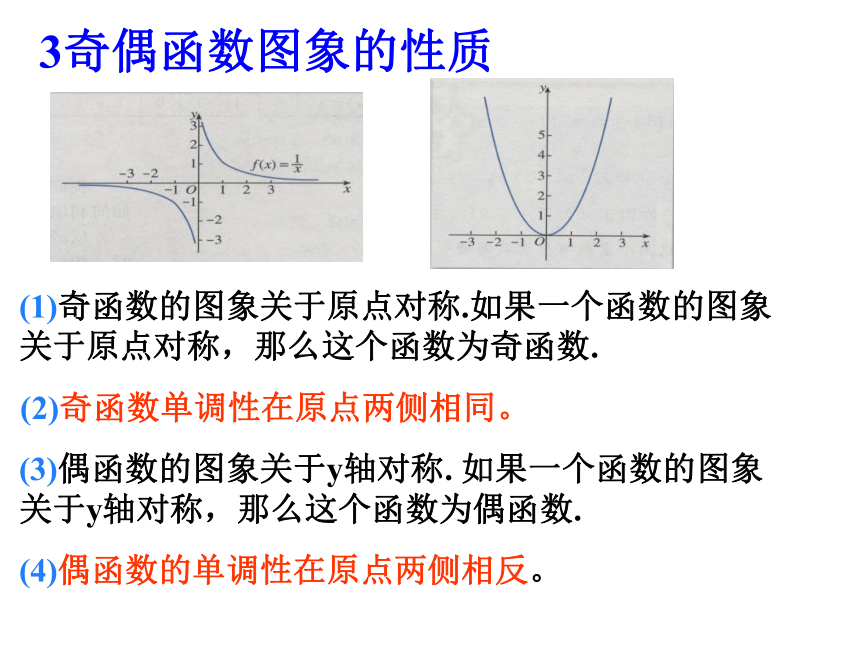
3奇偶函数图象的性质
(1)奇函数的图象关于原点对称.如果一个函数的图象关于原点对称,那么这个函数为奇函数.
(3)偶函数的图象关于y轴对称. 如果一个函数的图象关于y轴对称,那么这个函数为偶函数.
(2)奇函数单调性在原点两侧相同。
(4)偶函数的单调性在原点两侧相反。
例1. 判断下列函数的奇偶性
(1) f(x)=x3+2x; (2) f(x)=2x4+3x2;
解:
∵f(-x)=(-x)3+2(-x)
= -x3-2x
= -(x3+2x)
= - f(x),
∴f(x)为奇函数.
∵f(-x)=2(-x)4+3(-x)2
=2x4+3x2
∴f(x)为偶函数.
函数定义域为R.
解:
函数定义域为R.
= f(x),
巩固双基
解:函数定义域为R.
∴f(x)为奇函数.
有既是奇函数又是偶函数的吗?
解:函数定义域为 [0 ,+∞).
∵定义域不关于原点对称
∴f(x)为非奇非偶函数.
-2
3
0
x
y
(6) f(x)=x+1
解:函数f(x)的定义域为R.
∵ f(-x)=f(x)=0,
又 f(-x)=-f(x)=0,
∴f(x)为既奇又偶函数.
(5)f(x)=0 (x R)
根据奇偶性,
函数可划分为四类:
奇函数;
偶函数;
既奇又偶函数;
非奇非偶函数.
解:函数定义域为R.
∵ f(-x)= -x+1,
- f(x)= -x-1,
∴f(-x)≠f(x),且f(-x)≠ –f(x).
∴f(x)为非奇非偶函数.
注:对于形如 f(x)=x n 的函数,
若n为偶数,则它为偶函数。
若n为奇数,则它为奇函数。
练习1.判断下列函数的奇偶性
∴f(x)为奇函数.
解:定义域为{x|x≠0},
即 f(-x)= - f(x),
(2)f(x)=5
解:f(x)的定义域为R.
∵ f(-x)=f(x)=5
y
o
x
5
∴f(x)为偶函数.
∴f(x)既是偶函数, 又是奇函数.
解:函数的定义域为{-1,1},
例2.若函数
是偶函数,求m的值及函数的单调区间。
(1)
(2)
(3)
(4)
偶函数
非奇非偶函数
奇函数
非奇非偶函数
小结
o
o
o
o
x
x
x
x
y
y
y
y
例3、判断下列函数的奇偶性
课堂小结
1. 奇函数和偶函数定义.
一个函数为奇函数 它的图象关于原点对称.
一个函数为偶函数 它的图象关于y 轴对称.
2.奇偶函数的性质:
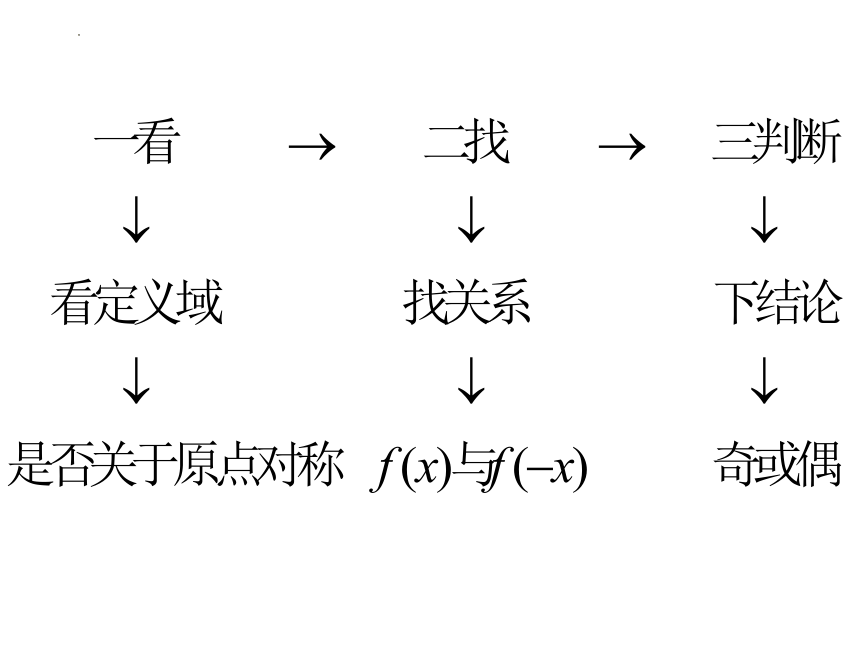
3.判断函数奇偶性的步骤
①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.
作业、
1、书P85练习的第2题
2、书P86复习巩固的第5题
(第一册) 第三章 函数的概念与性质
函数的基本性质
函数的奇偶性(第二课时)
2022年10月3日星期一
21
人教A版(2019)必修第一册
【学习重点】
【学习目标】
【学习难点】
学习目标
奇函数图象的对称性
了解函数的奇偶性与图象的对称性之间的关系
偶函数图象的对称性
奇偶函数图象的性质;
熟练解决函数单调性、奇偶性综合问题.
复习回顾
1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x) f(x)为奇函数.
如果都有f(-x)=f(x) f(x)为偶函数.
一个函数为奇函数 它的图象关于原点对称.
一个函数为偶函数 它的图象关于y 轴对称.
2.两个性质:
4.判断函数奇偶性的步骤
①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.
3、奇偶性与单调性的关系
奇函数在关于原点对称的区间上具有相同的单调性;
偶函数在关于原点对称的区间上具有相反的单调性.
【1】已知函数f(x)=ax2+bx+c,(2a-3≤x≤1)是 偶函数,则a=___,b=____,c∈___.
1
0
R
课前热身
【2】对于奇函数f(x),若x能取到零,则f(0)=__.
0
【4】函数 是偶函数.
【3】对于定义在R上的函数 f (x),
下列判断是否正确?
若f (-2) = f (2),则函数 f (x)是偶函数.
若f (-2)≠f (2),则函数 f (x)不是偶函数.
函数的奇偶性可用于:
(1)求函数的解析式
(2)简化函数图象的画法
(3)判断函数的单调性
(4)比较函数值的大小
(5)求参数的取值范围
例题讲解
(一)求函数的解析式
练习1、已知 f(x) 是定义在R上的奇函数,当x>0时, f(x)=x2+x-1, 求函数f(x)的表达式.
引申:如果改为偶函数呢?
x
y
o
例2.若 f(x) 为偶函数,g(x)为奇函数,且 求 f(x), g(x).
例3、已知函数的右半部分图象,根据下列条件把函数图象补充完整;
f(x)是偶函数; 2) f(x)是奇函数.
x
y
O
1
2
x
y
O
1
3
2
-1
B
A
(二)简化函数图象的画法
练习2、已知函数y=f(x)是偶函数,它在y轴右边的 图象如图,画出y=f(x)在 y轴左边的图象.
解:
o
y
x
练习3:如果奇函数f(x)在区间[3,7]上为增函数,且最小值是5,则在区间[-7,-3]上有没有最大值?是多少?
解:如图所示
函数有最大值
-7
-3
-5
3
5
x
y
7
o
函数f(x)在区间[-7,-3]上为增函数.
(三)比较函数值的大小
(四)求参数的取值范围
练习.定义在[-1,1]上的函数f(x) 是奇函数,并且在[-1,1] 上f(x)是增函数,求满足条件 f(1-a)+ f(1-a2)≤0的 a 的取值范围.
解:由f(1-a)+f(1-a2)≤0,
∵ f (x)是奇函数,
∵f(x)在[-1,1]上是增函数,
-2
2
0
1
故 a 的取值范围为
课堂小结
1.函数奇偶性的定义.
定义法
利用性质
2.函数奇偶性的判定
图象法:画出函数图象
①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.
拓展1:若对一切实数x, y 都有
(1)求f(0)的值;
(2)判定f(x)的奇偶性。
令 x = y = 0, 则
令y = -x , 则
故 f (x)是奇函数.
解:因为对于任何实数 x, y 都有
练习.已知函数 f (x) 对于任何实数 x, y 都有 f (x+y)+f(x-y)=2f (x) f (y) 且 f (0)≠0.
求证: f (x) 是偶函数.
令 x = y = 0, 则
令 x = 0 , 则
故 f (x)是偶函数.
解:已知函数 f (x) 对于任何实数 x, y 都有 f (x+y)+f(x-y)=2f (x) f (y),
课后巩固提高
1.奇函数 是定义在(-2,2)上的减函数,
若 求实数 的取值范围
2. 已知f(x)是R上的奇函数,且当x>0时,
求f(x)的解析式。
3. 函数 是定义在(-1,1)上的奇
函数,且 。
(1)求f(x)的解析式;
(2) 证明f(x)在(-1,1)上是增函数;
(3) 解不等式f(t-1)+f(t)<0.
(第一册) 第三章 函数的概念与性质
函数的基本性质
函数的奇偶性(第一课时)
2022年10月3日星期一
1
人教A版(2019)必修第一册
【学习目标】
奇函数的概念;
偶函数的概念;
函数奇偶性的判断;
【学习重点】
函数奇偶性的概念
【学习难点】
函数奇偶性的判断
【自学指导】阅读课本P82-84思考下列问题
1、奇函数与偶函数的概念分别是什么?
2、奇函数与偶函数的图像分别有什么特征?
3、判断函数的奇偶性的步骤是什么?
引入
引 例
1.已知函数f(x)=x2,求f(-2),f(2), f(-1),f(1),及f(-x) ,并画出y=f(-x)的图象.
解:
f(-2)=(-2)2=4 f(2)=4
f(-2)=f(2)
f(-1)=(-1)2=1 f(1)=1
f(-1)=f(1)
f(-x)=(-x)2=x2
f(-x)=f(x)
思考 :(1)这两个函数图象有什么共同特征吗?
(2)从解析式上如何体现上述特征?
偶函数的特征:
①解析式的基本特征:
f (-x)=f (x)
②图像特征:关于y轴对称.
如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数。
1. 偶函数的概念
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),
f(-1),f(1)及f(-x)
解:
f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)
f(-1)=(-1)3=-1, f(1)=1 f(-1)= - f(1)
f(-x)=(-x)3=-x3 f(-x)=- f(x)
思考 : 通过练习,你发现了什么规律
(-x,-y)
(x,y)
奇函数的特征:
①解析式的基本特征:
f (-x)=-f (x)
②图像特征:关于原点对称.
如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数。
2.奇函数的概念
如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.
3.奇偶性的概念
(1)若f(x)为奇函数, 则f(-x)=-f(x)成立.
若f(x)为偶函数, 则f(-x)= f(x) 成立.
(2)判断函数是否具有奇偶性.首先要看函数的定义域是否关于原点对称,即函数定义域关于原点对称是函数具有奇偶性的前提.
注意事项
[a ,b]
[-b,-a]
x
o
(3)函数的奇偶性是函数的整体性质;而函数的单调性是函数的局部性质.
奇函数的图象(如y=x3 )
偶函数的图象(如y=x2)
y
x
o
a
a
P/(-a ,f(-a))
p(a ,f(a))
-a
y
x
o
a
P/(-a ,f(-a))
p(a ,f(a))
-a
奇偶函数的图像
3奇偶函数图象的性质
(1)奇函数的图象关于原点对称.如果一个函数的图象关于原点对称,那么这个函数为奇函数.
(3)偶函数的图象关于y轴对称. 如果一个函数的图象关于y轴对称,那么这个函数为偶函数.
(2)奇函数单调性在原点两侧相同。
(4)偶函数的单调性在原点两侧相反。
例1. 判断下列函数的奇偶性
(1) f(x)=x3+2x; (2) f(x)=2x4+3x2;
解:
∵f(-x)=(-x)3+2(-x)
= -x3-2x
= -(x3+2x)
= - f(x),
∴f(x)为奇函数.
∵f(-x)=2(-x)4+3(-x)2
=2x4+3x2
∴f(x)为偶函数.
函数定义域为R.
解:
函数定义域为R.
= f(x),
巩固双基
解:函数定义域为R.
∴f(x)为奇函数.
有既是奇函数又是偶函数的吗?
解:函数定义域为 [0 ,+∞).
∵定义域不关于原点对称
∴f(x)为非奇非偶函数.
-2
3
0
x
y
(6) f(x)=x+1
解:函数f(x)的定义域为R.
∵ f(-x)=f(x)=0,
又 f(-x)=-f(x)=0,
∴f(x)为既奇又偶函数.
(5)f(x)=0 (x R)
根据奇偶性,
函数可划分为四类:
奇函数;
偶函数;
既奇又偶函数;
非奇非偶函数.
解:函数定义域为R.
∵ f(-x)= -x+1,
- f(x)= -x-1,
∴f(-x)≠f(x),且f(-x)≠ –f(x).
∴f(x)为非奇非偶函数.
注:对于形如 f(x)=x n 的函数,
若n为偶数,则它为偶函数。
若n为奇数,则它为奇函数。
练习1.判断下列函数的奇偶性
∴f(x)为奇函数.
解:定义域为{x|x≠0},
即 f(-x)= - f(x),
(2)f(x)=5
解:f(x)的定义域为R.
∵ f(-x)=f(x)=5
y
o
x
5
∴f(x)为偶函数.
∴f(x)既是偶函数, 又是奇函数.
解:函数的定义域为{-1,1},
例2.若函数
是偶函数,求m的值及函数的单调区间。
(1)
(2)
(3)
(4)
偶函数
非奇非偶函数
奇函数
非奇非偶函数
小结
o
o
o
o
x
x
x
x
y
y
y
y
例3、判断下列函数的奇偶性
课堂小结
1. 奇函数和偶函数定义.
一个函数为奇函数 它的图象关于原点对称.
一个函数为偶函数 它的图象关于y 轴对称.
2.奇偶函数的性质:
3.判断函数奇偶性的步骤
①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.
作业、
1、书P85练习的第2题
2、书P86复习巩固的第5题
(第一册) 第三章 函数的概念与性质
函数的基本性质
函数的奇偶性(第二课时)
2022年10月3日星期一
21
人教A版(2019)必修第一册
【学习重点】
【学习目标】
【学习难点】
学习目标
奇函数图象的对称性
了解函数的奇偶性与图象的对称性之间的关系
偶函数图象的对称性
奇偶函数图象的性质;
熟练解决函数单调性、奇偶性综合问题.
复习回顾
1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x) f(x)为奇函数.
如果都有f(-x)=f(x) f(x)为偶函数.
一个函数为奇函数 它的图象关于原点对称.
一个函数为偶函数 它的图象关于y 轴对称.
2.两个性质:
4.判断函数奇偶性的步骤
①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.
3、奇偶性与单调性的关系
奇函数在关于原点对称的区间上具有相同的单调性;
偶函数在关于原点对称的区间上具有相反的单调性.
【1】已知函数f(x)=ax2+bx+c,(2a-3≤x≤1)是 偶函数,则a=___,b=____,c∈___.
1
0
R
课前热身
【2】对于奇函数f(x),若x能取到零,则f(0)=__.
0
【4】函数 是偶函数.
【3】对于定义在R上的函数 f (x),
下列判断是否正确?
若f (-2) = f (2),则函数 f (x)是偶函数.
若f (-2)≠f (2),则函数 f (x)不是偶函数.
函数的奇偶性可用于:
(1)求函数的解析式
(2)简化函数图象的画法
(3)判断函数的单调性
(4)比较函数值的大小
(5)求参数的取值范围
例题讲解
(一)求函数的解析式
练习1、已知 f(x) 是定义在R上的奇函数,当x>0时, f(x)=x2+x-1, 求函数f(x)的表达式.
引申:如果改为偶函数呢?
x
y
o
例2.若 f(x) 为偶函数,g(x)为奇函数,且 求 f(x), g(x).
例3、已知函数的右半部分图象,根据下列条件把函数图象补充完整;
f(x)是偶函数; 2) f(x)是奇函数.
x
y
O
1
2
x
y
O
1
3
2
-1
B
A
(二)简化函数图象的画法
练习2、已知函数y=f(x)是偶函数,它在y轴右边的 图象如图,画出y=f(x)在 y轴左边的图象.
解:
o
y
x
练习3:如果奇函数f(x)在区间[3,7]上为增函数,且最小值是5,则在区间[-7,-3]上有没有最大值?是多少?
解:如图所示
函数有最大值
-7
-3
-5
3
5
x
y
7
o
函数f(x)在区间[-7,-3]上为增函数.
(三)比较函数值的大小
(四)求参数的取值范围
练习.定义在[-1,1]上的函数f(x) 是奇函数,并且在[-1,1] 上f(x)是增函数,求满足条件 f(1-a)+ f(1-a2)≤0的 a 的取值范围.
解:由f(1-a)+f(1-a2)≤0,
∵ f (x)是奇函数,
∵f(x)在[-1,1]上是增函数,
-2
2
0
1
故 a 的取值范围为
课堂小结
1.函数奇偶性的定义.
定义法
利用性质
2.函数奇偶性的判定
图象法:画出函数图象
①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.
拓展1:若对一切实数x, y 都有
(1)求f(0)的值;
(2)判定f(x)的奇偶性。
令 x = y = 0, 则
令y = -x , 则
故 f (x)是奇函数.
解:因为对于任何实数 x, y 都有
练习.已知函数 f (x) 对于任何实数 x, y 都有 f (x+y)+f(x-y)=2f (x) f (y) 且 f (0)≠0.
求证: f (x) 是偶函数.
令 x = y = 0, 则
令 x = 0 , 则
故 f (x)是偶函数.
解:已知函数 f (x) 对于任何实数 x, y 都有 f (x+y)+f(x-y)=2f (x) f (y),
课后巩固提高
1.奇函数 是定义在(-2,2)上的减函数,
若 求实数 的取值范围
2. 已知f(x)是R上的奇函数,且当x>0时,
求f(x)的解析式。
3. 函数 是定义在(-1,1)上的奇
函数,且 。
(1)求f(x)的解析式;
(2) 证明f(x)在(-1,1)上是增函数;
(3) 解不等式f(t-1)+f(t)<0.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
