数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质(1)课件(16张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质(1)课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 291.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 13:01:13 | ||
图片预览






文档简介
(共16张PPT)
3.2.2双曲线的简单几何性质(1)
范围:
图像法:
代数法:
对称性:
双曲线的对称中心叫做双曲线的中心.
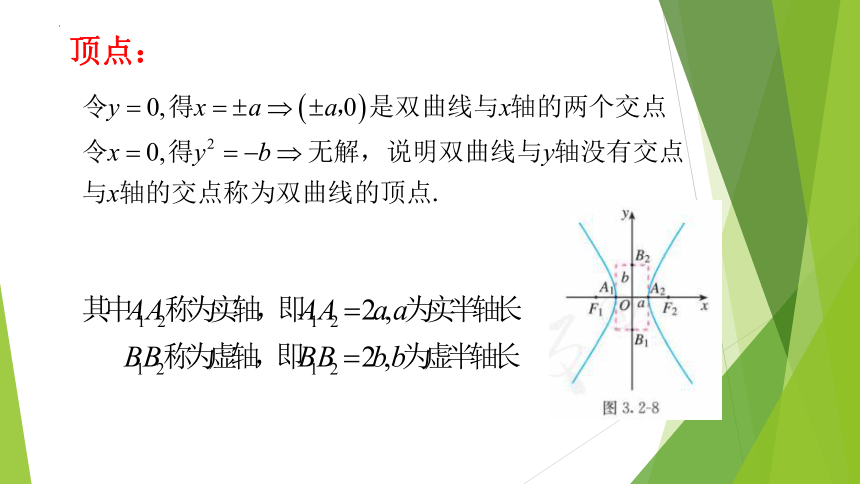
顶点:
渐近线:(双曲线特有的)
离心率:
总结:
坐标轴
原点
题型一:双曲线的简单几何性质
总结:
(1)把方程写成双曲线的标准方程
(2)写出a与b的值,从而求出c
(3)写出所求的双曲线的几何性质
注意:区分实轴与实半轴,虚轴与虚半轴
题型二:由几何性质求双曲线的标准方程
总结:
(1)先确定焦点的位置,设方程
(2)根据题意求出
(3)最后写出所求的双曲线方程
题型三:求双曲线的离心率的值或范围
总结:
求双曲线离心率的值或范围的步骤:
1,根据题意建立关于a,b,c的关系
2,利用双曲线的几何性质构建齐次方程或不等式
3,采用同除以a的最高次幂的方法得到关于离心率的方程或不等式
4,解方程或不等式从而得到结果
课堂小结:
1,从范围,对称性,顶点,渐近线,离心率角度了解双曲线的简单几何性质
2,能指出双曲线的几何性质,并利用双曲线的几何性质求双曲线的标准方程
3,掌握求双曲线离心率的方法
课堂检测:
3.2.2双曲线的简单几何性质(1)
范围:
图像法:
代数法:
对称性:
双曲线的对称中心叫做双曲线的中心.
顶点:
渐近线:(双曲线特有的)
离心率:
总结:
坐标轴
原点
题型一:双曲线的简单几何性质
总结:
(1)把方程写成双曲线的标准方程
(2)写出a与b的值,从而求出c
(3)写出所求的双曲线的几何性质
注意:区分实轴与实半轴,虚轴与虚半轴
题型二:由几何性质求双曲线的标准方程
总结:
(1)先确定焦点的位置,设方程
(2)根据题意求出
(3)最后写出所求的双曲线方程
题型三:求双曲线的离心率的值或范围
总结:
求双曲线离心率的值或范围的步骤:
1,根据题意建立关于a,b,c的关系
2,利用双曲线的几何性质构建齐次方程或不等式
3,采用同除以a的最高次幂的方法得到关于离心率的方程或不等式
4,解方程或不等式从而得到结果
课堂小结:
1,从范围,对称性,顶点,渐近线,离心率角度了解双曲线的简单几何性质
2,能指出双曲线的几何性质,并利用双曲线的几何性质求双曲线的标准方程
3,掌握求双曲线离心率的方法
课堂检测:
