13.3.2 等腰三角形判定课件(20张PPT)
文档属性
| 名称 | 13.3.2 等腰三角形判定课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-03 17:54:14 | ||
图片预览








文档简介
(共20张PPT)
13.3.2 等腰三角形判定
华师大版 八年级上册
教学目标
1.等腰三角形的判定.
2.等边三角形的判定.
3.等腰三角形的性质与判定的综合运用.
【教学重点】等腰三角形(含等边三角形)的判定.
【教学难点】等腰三角形的性质与判定的综合运用.
复习导入
A
B
C
等腰三角形的性质:
等腰三角形两腰相等。
等腰三角形两底角相等(等边对等角)。
等腰三角形底边上的高、中线及顶角的平分线互相重合(三线合一)。
等腰三角形是轴对称图形。
新知讲解
探索
我们知道,等腰三角形的两个底角相等.反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?
画画看,你发现了什么?
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
如何证明这一结论?
新知讲解
A
B
C
设法构造两个全等三角形.
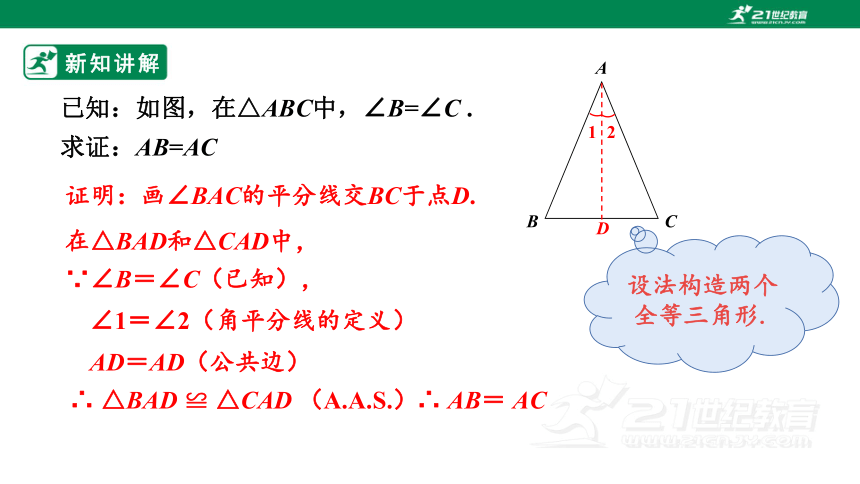
已知:如图,在△ABC中,∠B=∠C .
求证:AB=AC
∴ AB= AC
∵∠B=∠C(已知),
∴ △BAD ≌ △CAD (A.A.S.)
AD=AD(公共边)
证明:画∠BAC的平分线交BC于点D.
在△BAD和△CAD中,
∠1=∠2(角平分线的定义)
1
2
D
新知讲解
A
B
C
如果一个三角形有两个角相等,那么这两个角所对的边也相等.
(简写成“等角对等边”)。
符号语言:
∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
巩固练习
1. 如图,∠A = 72°,∠B = 36°,CD平分∠ACB.试指出图中的哪些三角形是等腰三角形,并说明理由.
A
B
C
D
72°
36°
72°
36°
36°
∠ACB=72°
∠BCD=∠ACD=36°
△ACD,△BCD,△ABC都是等腰三角形。
教材84页第1题
例题讲解
A
C
B
40°
例1 如图,在△ABC中,已知∠A = 40°,∠B = 70°.求证:AB = AC.
70°
证明:∵ ∠ A+ ∠ B+ ∠ C =180°(三角形的内角和等于180°),
∠A = 40°,∠ B = 70°(已知),
∴ ∠C = 180° - ∠ A- ∠ B(等式的性质),
= 180°- 40°- 70° = 70°,
∴ ∠ C = ∠ B(等量代换),
∴ AB = AC(等角对等边).
巩固练习
2. 如图,AB = DC,∠ABC = ∠DCB,AC、BD相交于点E. 求证:EB =EC.
B
A
E
D
C
证明: 在△ABC和△DCB中,
∵ AB=DC,
∠ABC=∠DCB,
BC=CB,
∴ △ABC≌△DCB(S.A.S.),
∴ ∠ECB=∠EBC,
∴ EB=EC.
教材84页第2题
新知讲解
A
B
C
由“等角对等边”可知:
三个角都相等的三角形是等边三角形.
有一个角等于60°的等腰三角形是等边三角形.
顶角、底角都可判定
巩固练习
3.如图,已知D为BC的中点,DE ⊥AB,DF ⊥ AC,点E、F为垂足,且 BE = CF,∠BDE =30°.求证:△ABC是等边三角形.
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在 Rt△BDE和 Rt△CDF中,
BD=CD,BE=CF,
∴Rt△BDE≌Rt△CDF(H.L.),
教材85页第7题
∴∠B=∠C.∴AB=AC.
又∵∠BDE=30°,∴ ∠B=∠C=60°,
∴△ ABC是等边三角形.
例题讲解
例2 如图,AB// CD, ∠ 1 = ∠ 2.求证:AB = AC.
A
C
B
分析 要证AB = AC,可以设法证明∠ B= ∠ 1 ,而∠ 1 = ∠ 2,因此只要证明∠ B = ∠ 2.
1 2
D
证明:
∵ AB// CD(已知),
∴ ∠ B= ∠ 2(两直线平行,同位角相等).
又∵ ∠ 1 = ∠ 2(已知),
∴∠ B = ∠ 1(等量代换),
∴ AB = AC(等角对等边).
例题讲解
例3 如图,在Rt △ABC和Rt △ A'B'C'中,∠ACB=∠A'C'B'= 90°,AB = A'B',AC =A'C'.求证:Rt△ABC≌Rt△A'B'C'.
-------------------
--------------------------------
A
C
B
A' (A)
C'(C)
B'
B
证明:由于直角边AC = A'C',
我们移动Rt△ABC,使点A与点A'、点C与点C'重合,且使点B与点B'分别位于A'C'的两侧.
∵ ∠A'C'B = ∠A'C'B'=90°(已知),
∴∠B'C'B= ∠A'C'B'+ ∠A'C'B = 180°,
即点B'、C'、B在同一条直线上.
例题讲解
在△A'B'B中,
∵A'B'=AB = A'B(已知),
∠ B = ∠ B'(等边对等角).
在△ABC和△A'B'C'中,
∵ ∠ B=∠ B'(已证),
∠ ACB=∠ A'C'B'(已知),
AC=A'C'(已知),
∴Rt△ABC≌Rt△A'B'C'(A.A.S.).
这样,我们就证明了前面已给出的直角三角形全等的H.L.判定定理.
巩固练习
4. 如图所示的三角测平架中,AB = AC,在BC的中点D挂一个重锤,自然下垂.调整架身,使点A恰好在重锤线上.试问:此时BC是否正好处于水平位置?为什么?
解:在.
∵AB=AC,BD=DC,
∴AD⊥BC.
而AD与水平线垂直,所以BC在水平位置.
教材85页第8题
课堂总结
等腰三角形
判定→等角对等边
应用→证明同一个三角形中两边相等
等边三角形→判定方法
证三个角都相等或有两个角等于60°
先证等腰三角形,再证有一个角等于60°
随堂练习
1. 如图,∠A = ∠B,CE∥DA. 求证:CE = CB. 需再增加什么条件,可使△BCE成为等边三角形
B
A
D
C
E
证明: ∵CE∥DA,
∴∠A=∠CEB .
∵∠A=∠B,
∴∠CEB=∠B,
∴CE=CB .
再增加∠B=60°,可使△BCE成为等边三角形(答案不唯一)
随堂练习
2. 如图,在△ABC中,∠ACB=900,点D在BC的延长线上,点E在边AB上,连结DE交AC于点F,若AE=EF,求证:△BDE为等腰三角形。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.3.2 等腰三角形判定
华师大版 八年级上册
教学目标
1.等腰三角形的判定.
2.等边三角形的判定.
3.等腰三角形的性质与判定的综合运用.
【教学重点】等腰三角形(含等边三角形)的判定.
【教学难点】等腰三角形的性质与判定的综合运用.
复习导入
A
B
C
等腰三角形的性质:
等腰三角形两腰相等。
等腰三角形两底角相等(等边对等角)。
等腰三角形底边上的高、中线及顶角的平分线互相重合(三线合一)。
等腰三角形是轴对称图形。
新知讲解
探索
我们知道,等腰三角形的两个底角相等.反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?
画画看,你发现了什么?
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
如何证明这一结论?
新知讲解
A
B
C
设法构造两个全等三角形.
已知:如图,在△ABC中,∠B=∠C .
求证:AB=AC
∴ AB= AC
∵∠B=∠C(已知),
∴ △BAD ≌ △CAD (A.A.S.)
AD=AD(公共边)
证明:画∠BAC的平分线交BC于点D.
在△BAD和△CAD中,
∠1=∠2(角平分线的定义)
1
2
D
新知讲解
A
B
C
如果一个三角形有两个角相等,那么这两个角所对的边也相等.
(简写成“等角对等边”)。
符号语言:
∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
巩固练习
1. 如图,∠A = 72°,∠B = 36°,CD平分∠ACB.试指出图中的哪些三角形是等腰三角形,并说明理由.
A
B
C
D
72°
36°
72°
36°
36°
∠ACB=72°
∠BCD=∠ACD=36°
△ACD,△BCD,△ABC都是等腰三角形。
教材84页第1题
例题讲解
A
C
B
40°
例1 如图,在△ABC中,已知∠A = 40°,∠B = 70°.求证:AB = AC.
70°
证明:∵ ∠ A+ ∠ B+ ∠ C =180°(三角形的内角和等于180°),
∠A = 40°,∠ B = 70°(已知),
∴ ∠C = 180° - ∠ A- ∠ B(等式的性质),
= 180°- 40°- 70° = 70°,
∴ ∠ C = ∠ B(等量代换),
∴ AB = AC(等角对等边).
巩固练习
2. 如图,AB = DC,∠ABC = ∠DCB,AC、BD相交于点E. 求证:EB =EC.
B
A
E
D
C
证明: 在△ABC和△DCB中,
∵ AB=DC,
∠ABC=∠DCB,
BC=CB,
∴ △ABC≌△DCB(S.A.S.),
∴ ∠ECB=∠EBC,
∴ EB=EC.
教材84页第2题
新知讲解
A
B
C
由“等角对等边”可知:
三个角都相等的三角形是等边三角形.
有一个角等于60°的等腰三角形是等边三角形.
顶角、底角都可判定
巩固练习
3.如图,已知D为BC的中点,DE ⊥AB,DF ⊥ AC,点E、F为垂足,且 BE = CF,∠BDE =30°.求证:△ABC是等边三角形.
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在 Rt△BDE和 Rt△CDF中,
BD=CD,BE=CF,
∴Rt△BDE≌Rt△CDF(H.L.),
教材85页第7题
∴∠B=∠C.∴AB=AC.
又∵∠BDE=30°,∴ ∠B=∠C=60°,
∴△ ABC是等边三角形.
例题讲解
例2 如图,AB// CD, ∠ 1 = ∠ 2.求证:AB = AC.
A
C
B
分析 要证AB = AC,可以设法证明∠ B= ∠ 1 ,而∠ 1 = ∠ 2,因此只要证明∠ B = ∠ 2.
1 2
D
证明:
∵ AB// CD(已知),
∴ ∠ B= ∠ 2(两直线平行,同位角相等).
又∵ ∠ 1 = ∠ 2(已知),
∴∠ B = ∠ 1(等量代换),
∴ AB = AC(等角对等边).
例题讲解
例3 如图,在Rt △ABC和Rt △ A'B'C'中,∠ACB=∠A'C'B'= 90°,AB = A'B',AC =A'C'.求证:Rt△ABC≌Rt△A'B'C'.
-------------------
--------------------------------
A
C
B
A' (A)
C'(C)
B'
B
证明:由于直角边AC = A'C',
我们移动Rt△ABC,使点A与点A'、点C与点C'重合,且使点B与点B'分别位于A'C'的两侧.
∵ ∠A'C'B = ∠A'C'B'=90°(已知),
∴∠B'C'B= ∠A'C'B'+ ∠A'C'B = 180°,
即点B'、C'、B在同一条直线上.
例题讲解
在△A'B'B中,
∵A'B'=AB = A'B(已知),
∠ B = ∠ B'(等边对等角).
在△ABC和△A'B'C'中,
∵ ∠ B=∠ B'(已证),
∠ ACB=∠ A'C'B'(已知),
AC=A'C'(已知),
∴Rt△ABC≌Rt△A'B'C'(A.A.S.).
这样,我们就证明了前面已给出的直角三角形全等的H.L.判定定理.
巩固练习
4. 如图所示的三角测平架中,AB = AC,在BC的中点D挂一个重锤,自然下垂.调整架身,使点A恰好在重锤线上.试问:此时BC是否正好处于水平位置?为什么?
解:在.
∵AB=AC,BD=DC,
∴AD⊥BC.
而AD与水平线垂直,所以BC在水平位置.
教材85页第8题
课堂总结
等腰三角形
判定→等角对等边
应用→证明同一个三角形中两边相等
等边三角形→判定方法
证三个角都相等或有两个角等于60°
先证等腰三角形,再证有一个角等于60°
随堂练习
1. 如图,∠A = ∠B,CE∥DA. 求证:CE = CB. 需再增加什么条件,可使△BCE成为等边三角形
B
A
D
C
E
证明: ∵CE∥DA,
∴∠A=∠CEB .
∵∠A=∠B,
∴∠CEB=∠B,
∴CE=CB .
再增加∠B=60°,可使△BCE成为等边三角形(答案不唯一)
随堂练习
2. 如图,在△ABC中,∠ACB=900,点D在BC的延长线上,点E在边AB上,连结DE交AC于点F,若AE=EF,求证:△BDE为等腰三角形。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
