北师大版八年级上册3.1 确定位置课件(共20张PPT)
文档属性
| 名称 | 北师大版八年级上册3.1 确定位置课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 20:24:27 | ||
图片预览







文档简介
(共20张PPT)
北师大版数学 八年级上册
第三章 位置与坐标
教学课件
1.确定位置
教学目标
第三章 位置与坐标
1.知道在平面内,确定物体的位置需要两个数据.(重点)
2.掌握平面内的行列定位法、方位角加距离定位法、经纬定位法等定位方法.(难点)
教学过程——温故知新
第三章 位置与坐标
平面内,如何确定物体的方位角?
教学过程——新课引入
第三章 位置与坐标
议一议
在茫茫的大海上,一艘轮船遭遇了强台风,船员发出了求救信号,一艘救援船接到信息后,如何确定遇险船只的位置?
sos...
收到...
教学过程——新知探究
第三章 位置与坐标
知识点1 利用行列定位
行列定位法
在电影院看电影时,我们的电影票上常常写着“X排X座”等字样,这实际上就是一种定位方法。
在平面内,用物体所在的行数和列数确定物体位置的方法称为行列定位法。
由此可见,用行列定位法确定物体的位置需要两个数据——行数和列数。
教学过程——新知探究
第三章 位置与坐标
知识点2 利用方位角加距离定位
方位角加距离定位法
在海上航行的两艘船,可以利用方位角加距离来确定彼此的位置。
在平面内,用物体所在的方向和距离确定物体位置的方法称为方向角加距离定位法。
北
78°
35海里
由此可见,用这种方法确定物体的位置同样需要两个数据——方位角和距离。
教学过程——新知探究
第三章 位置与坐标
知识点3 利用经度和纬度定位
经纬定位法
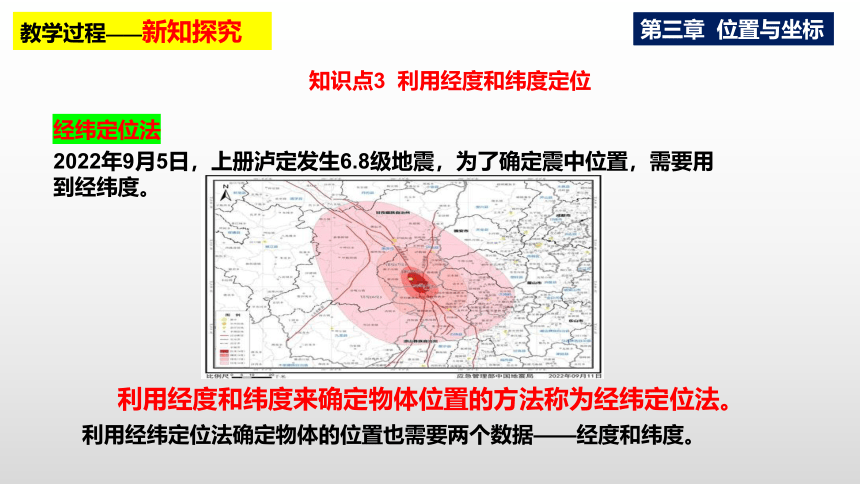
2022年9月5日,上册泸定发生6.8级地震,为了确定震中位置,需要用到经纬度。
利用经度和纬度来确定物体位置的方法称为经纬定位法。
利用经纬定位法确定物体的位置也需要两个数据——经度和纬度。
教学过程——新知探究
第三章 位置与坐标
知识点4 利用区域定位
区域定位法
有时我们只需要确定物体位置的大致区域,这时我们就可以用区域定位。
从上面的图中可知广州火车站在B3区,烈士陵园在C4区。
区域定位法也需要两个数据,区域定位是简单明了,但定位不够准确。
在平面内,确定一个物体的位置一般需要两个数据。
教学过程——学以致用
第三章 位置与坐标
做一做
1. 教室里将第2排第3列记为(2 , 3),那么第5排第4列记为( )
A. 5 B. 4 C. (4 , 5) D. (5 , 4)
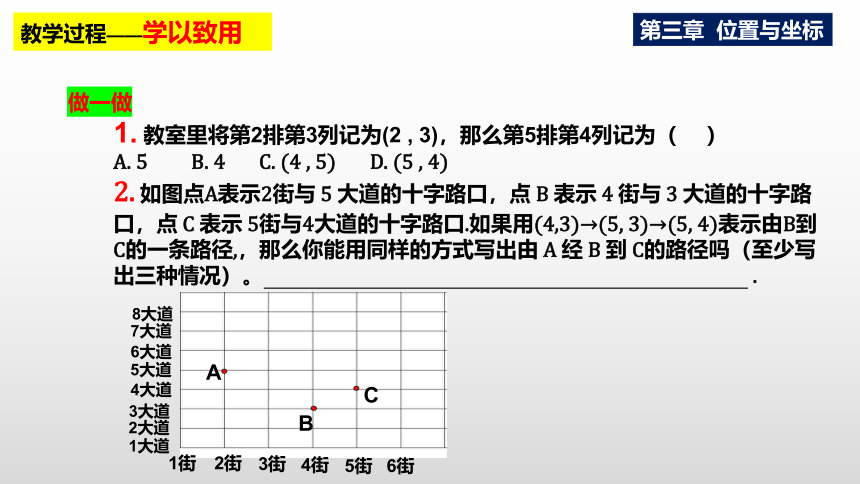
2. 如图点A表示2街与 5 大道的十字路口,点 B 表示 4 街与 3 大道的十字路口,点 C 表示 5街与4大道的十字路口.如果用(4,3)→(5, 3)→(5, 4)表示由B到C的一条路径,,那么你能用同样的方式写出由 A 经 B 到 C的路径吗(至少写出三种情况)。 .
1街
2街
3街
4街
5街
6街
1大道
2大道
3大道
4大道
5大道
6大道
7大道
8大道
A
B
C
教学过程——学以致用
第三章 位置与坐标
做一做
3. 文具店、书店和玩具店依次坐落在一条东西走向的大街上,文具店在书店西边 20m 处,玩具位于书店东边 100m 处,小明从书店沿街向东走了30m,接差着又向东走了-50m,此时小明位在( )
A.文具店 B.玩具店 C.文具店西 30m D.玩具店西 50m
4. 小刚家在学校的北偏东 30°方向,距离学校 2000m,则学校在小刚家 .
教学过程——典例精析
第三章 位置与坐标
听一听
典例1
如图,海上有 A.B.C三个小岛,测得 AC=30 千米,AB=50千米,B 岛在 C 岛北偏西 75°的方向上,距C岛40 千米,请你根据上述条件确定 C岛相对于 A岛的位置。
75°
教学过程——典例精析
第三章 位置与坐标
听一听
解:在△ABC中 ,BC2+AC2=402+302=2500,
AB2=502=2500
75°
∴BC2+AC2=AB2
∴△ABC为直角三角形
∴A岛位于C岛北偏东(90°-75°)方向.
∴C岛位于A岛南偏西15°方向,距离A岛30km处.
教学过程——典例精析
第三章 位置与坐标
听一听
典例2
如图,某风景区有A、B、C三个景点,已知景点C在景点 A 的正东方向 400 米处,景点 B 在景点C 的正北方向 400 米处,那么景点B在景点A的什么位置呢 。
教学过程——典例精析
第三章 位置与坐标
听一听
解:根据题意可知,∠C=90°,AC=BC=400
∴∠A=∠B=45°,AB=
=
∴点B位于点A北偏东45°方向,距离点A米处.
教学过程——典例精析
第三章 位置与坐标
听一听
典例3
如图 1,将射线 OX 按逆时针方向旋转β度角,得到射线 OY,如果点 P为射线 OY上的一点,且OP=,那么我们规定用(,β)表示点P在平面内的位置,并记为P(,β).例如,图 2 中,如果 OM=8,∠XOM=110°,那么点M在平面内的位置,记为M(8,110),根据图形,解答下列问题:
(1)如图 3,如果点N在平面内的位置记为 N(6,30),那么 ON= ,∠XON= .
(2)如果点 A、B在平面内的位置分别记为A(5,30),B(12,120),试求A、B两点之间的距离
N(6 , 30)
β
P
X
图1
O
110°
M(8 , 110)
X
图2
O
X
图3
O
教学过程——典例精析
第三章 位置与坐标
听一听
略解:(1)ON =6,∠XON=30°
(2)AB=
教学过程——回归课本
第三章 位置与坐标
做一做
完成课本第56页“随堂练习”
教学过程——课堂小结
第三章 位置与坐标
记一记
在平面内,确定有关物体的位置一般需要两个数据。
课后巩固——分层作业
第三章 位置与坐标
练一练
完成相关作业.
结束新课
感谢聆听
第三章 位置与坐标
北师大版数学 八年级上册
第三章 位置与坐标
教学课件
1.确定位置
教学目标
第三章 位置与坐标
1.知道在平面内,确定物体的位置需要两个数据.(重点)
2.掌握平面内的行列定位法、方位角加距离定位法、经纬定位法等定位方法.(难点)
教学过程——温故知新
第三章 位置与坐标
平面内,如何确定物体的方位角?
教学过程——新课引入
第三章 位置与坐标
议一议
在茫茫的大海上,一艘轮船遭遇了强台风,船员发出了求救信号,一艘救援船接到信息后,如何确定遇险船只的位置?
sos...
收到...
教学过程——新知探究
第三章 位置与坐标
知识点1 利用行列定位
行列定位法
在电影院看电影时,我们的电影票上常常写着“X排X座”等字样,这实际上就是一种定位方法。
在平面内,用物体所在的行数和列数确定物体位置的方法称为行列定位法。
由此可见,用行列定位法确定物体的位置需要两个数据——行数和列数。
教学过程——新知探究
第三章 位置与坐标
知识点2 利用方位角加距离定位
方位角加距离定位法
在海上航行的两艘船,可以利用方位角加距离来确定彼此的位置。
在平面内,用物体所在的方向和距离确定物体位置的方法称为方向角加距离定位法。
北
78°
35海里
由此可见,用这种方法确定物体的位置同样需要两个数据——方位角和距离。
教学过程——新知探究
第三章 位置与坐标
知识点3 利用经度和纬度定位
经纬定位法
2022年9月5日,上册泸定发生6.8级地震,为了确定震中位置,需要用到经纬度。
利用经度和纬度来确定物体位置的方法称为经纬定位法。
利用经纬定位法确定物体的位置也需要两个数据——经度和纬度。
教学过程——新知探究
第三章 位置与坐标
知识点4 利用区域定位
区域定位法
有时我们只需要确定物体位置的大致区域,这时我们就可以用区域定位。
从上面的图中可知广州火车站在B3区,烈士陵园在C4区。
区域定位法也需要两个数据,区域定位是简单明了,但定位不够准确。
在平面内,确定一个物体的位置一般需要两个数据。
教学过程——学以致用
第三章 位置与坐标
做一做
1. 教室里将第2排第3列记为(2 , 3),那么第5排第4列记为( )
A. 5 B. 4 C. (4 , 5) D. (5 , 4)
2. 如图点A表示2街与 5 大道的十字路口,点 B 表示 4 街与 3 大道的十字路口,点 C 表示 5街与4大道的十字路口.如果用(4,3)→(5, 3)→(5, 4)表示由B到C的一条路径,,那么你能用同样的方式写出由 A 经 B 到 C的路径吗(至少写出三种情况)。 .
1街
2街
3街
4街
5街
6街
1大道
2大道
3大道
4大道
5大道
6大道
7大道
8大道
A
B
C
教学过程——学以致用
第三章 位置与坐标
做一做
3. 文具店、书店和玩具店依次坐落在一条东西走向的大街上,文具店在书店西边 20m 处,玩具位于书店东边 100m 处,小明从书店沿街向东走了30m,接差着又向东走了-50m,此时小明位在( )
A.文具店 B.玩具店 C.文具店西 30m D.玩具店西 50m
4. 小刚家在学校的北偏东 30°方向,距离学校 2000m,则学校在小刚家 .
教学过程——典例精析
第三章 位置与坐标
听一听
典例1
如图,海上有 A.B.C三个小岛,测得 AC=30 千米,AB=50千米,B 岛在 C 岛北偏西 75°的方向上,距C岛40 千米,请你根据上述条件确定 C岛相对于 A岛的位置。
75°
教学过程——典例精析
第三章 位置与坐标
听一听
解:在△ABC中 ,BC2+AC2=402+302=2500,
AB2=502=2500
75°
∴BC2+AC2=AB2
∴△ABC为直角三角形
∴A岛位于C岛北偏东(90°-75°)方向.
∴C岛位于A岛南偏西15°方向,距离A岛30km处.
教学过程——典例精析
第三章 位置与坐标
听一听
典例2
如图,某风景区有A、B、C三个景点,已知景点C在景点 A 的正东方向 400 米处,景点 B 在景点C 的正北方向 400 米处,那么景点B在景点A的什么位置呢 。
教学过程——典例精析
第三章 位置与坐标
听一听
解:根据题意可知,∠C=90°,AC=BC=400
∴∠A=∠B=45°,AB=
=
∴点B位于点A北偏东45°方向,距离点A米处.
教学过程——典例精析
第三章 位置与坐标
听一听
典例3
如图 1,将射线 OX 按逆时针方向旋转β度角,得到射线 OY,如果点 P为射线 OY上的一点,且OP=,那么我们规定用(,β)表示点P在平面内的位置,并记为P(,β).例如,图 2 中,如果 OM=8,∠XOM=110°,那么点M在平面内的位置,记为M(8,110),根据图形,解答下列问题:
(1)如图 3,如果点N在平面内的位置记为 N(6,30),那么 ON= ,∠XON= .
(2)如果点 A、B在平面内的位置分别记为A(5,30),B(12,120),试求A、B两点之间的距离
N(6 , 30)
β
P
X
图1
O
110°
M(8 , 110)
X
图2
O
X
图3
O
教学过程——典例精析
第三章 位置与坐标
听一听
略解:(1)ON =6,∠XON=30°
(2)AB=
教学过程——回归课本
第三章 位置与坐标
做一做
完成课本第56页“随堂练习”
教学过程——课堂小结
第三章 位置与坐标
记一记
在平面内,确定有关物体的位置一般需要两个数据。
课后巩固——分层作业
第三章 位置与坐标
练一练
完成相关作业.
结束新课
感谢聆听
第三章 位置与坐标
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
