苏科版八年级上册3.1 勾股定理 课件 (共27张PPT)
文档属性
| 名称 | 苏科版八年级上册3.1 勾股定理 课件 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 16.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 20:51:13 | ||
图片预览


文档简介
(共27张PPT)
3.1勾股定理
相传2500年前,毕达哥拉斯应邀出席宴会,宴会厅中铺着美丽的等腰直角三角形地砖,这位善于观察的数学家从看似平淡无奇的现象中发现了“神奇而伟大的定理”。
这是1955年希腊曾经发行的纪念一位数学家的邮票。
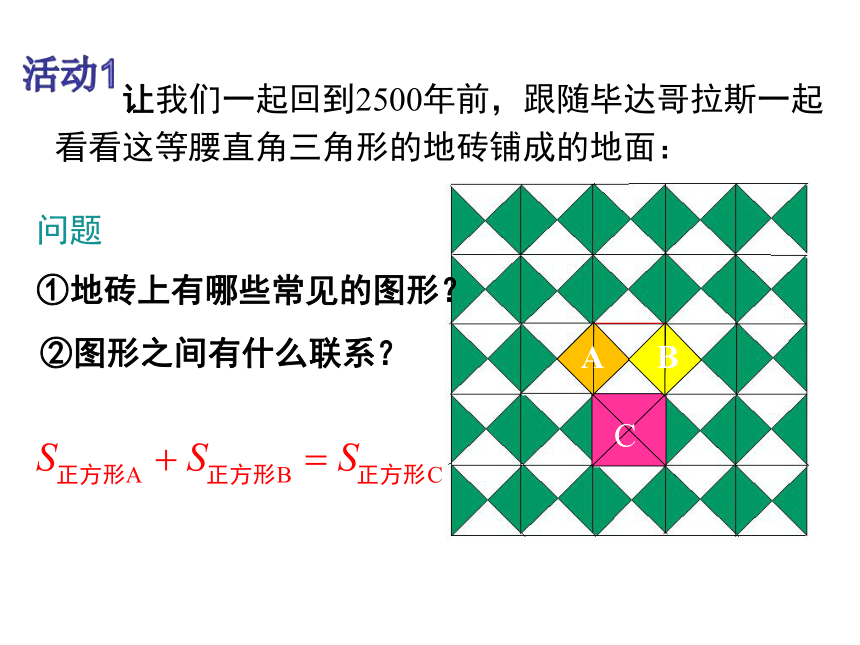
让我们一起回到2500年前,跟随毕达哥拉斯一起看看这等腰直角三角形的地砖铺成的地面:
A
B
C
问题
①地砖上有哪些常见的图形?
②图形之间有什么联系?
A
B
C
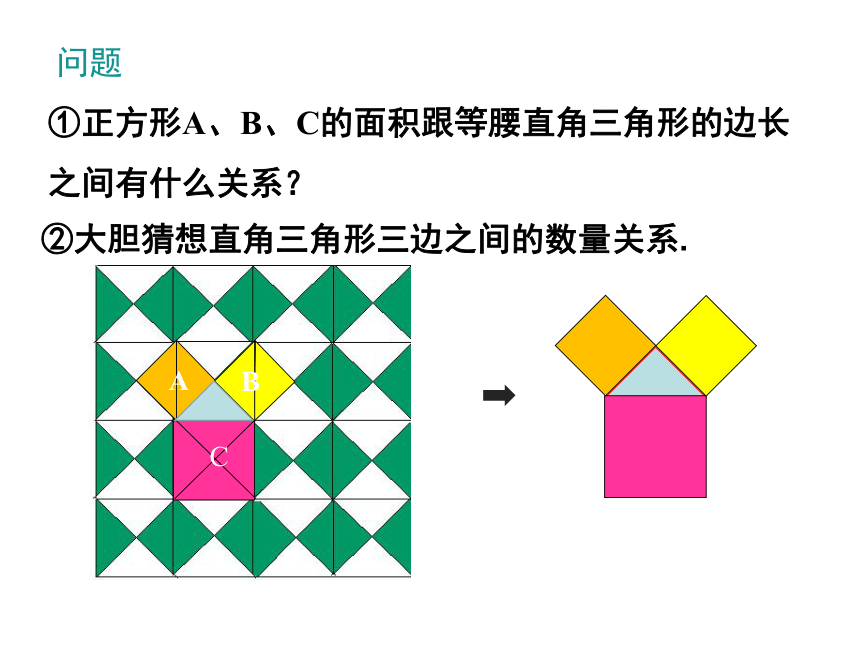
问题
①正方形A、B、C的面积跟等腰直角三角形的边长之间有什么关系?
②大胆猜想直角三角形三边之间的数量关系.
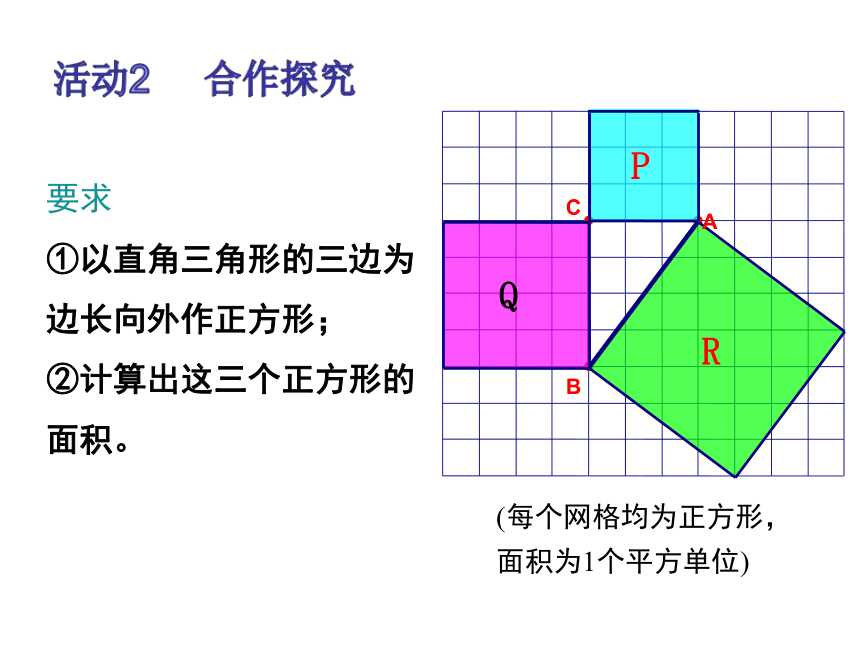
要求
①以直角三角形的三边为边长向外作正方形;
②计算出这三个正方形的面积。
P
Q
R
A
B
C
(每个网格均为正方形,
面积为1个平方单位)
P
Q
C
R
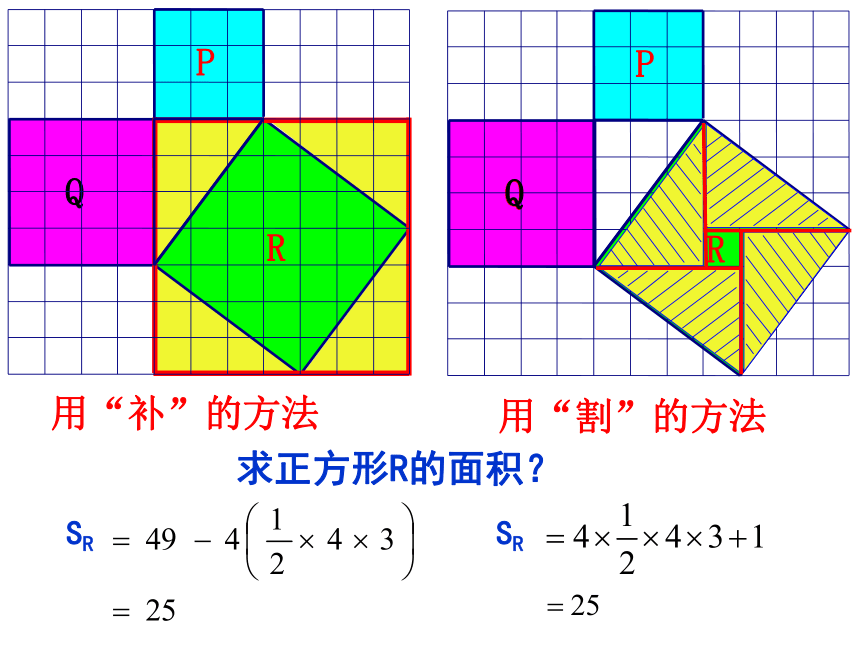
求正方形R的面积?
用“补”的方法
P
Q
C
R
用“割”的方法
Q
SR
SR
P
Q
R
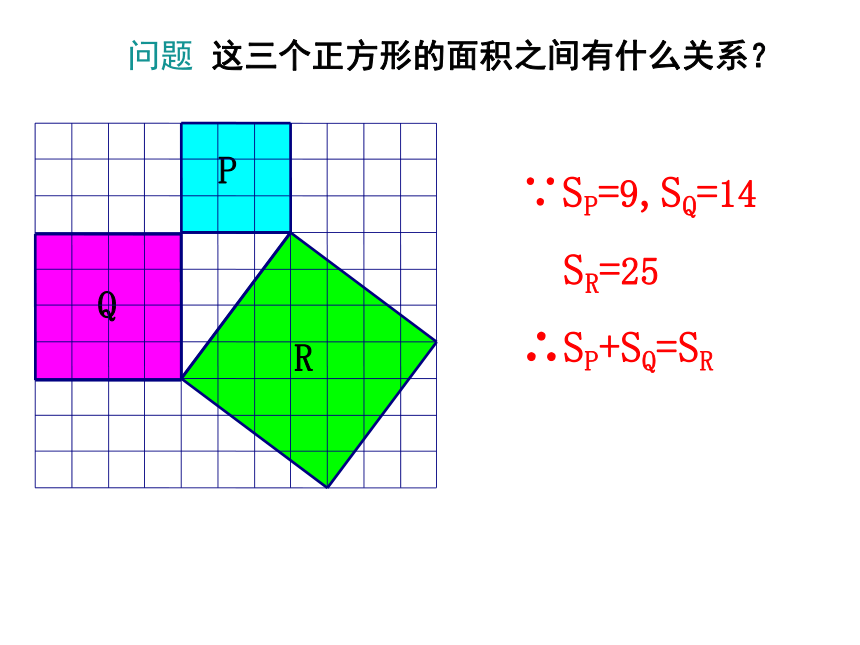
∵SP=9,SQ=14
SR=25
∴SP+SQ=SR
问题 这三个正方形的面积之间有什么关系?
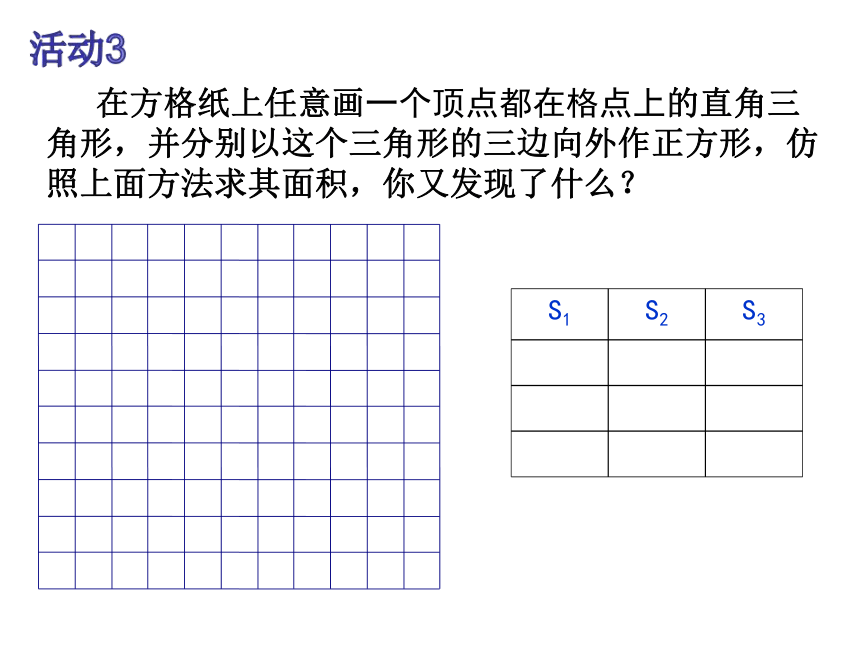
S1 S2 S3
在方格纸上任意画一个顶点都在格点上的直角三角形,并分别以这个三角形的三边向外作正方形,仿照上面方法求其面积,你又发现了什么?
A
B
C
图1--3
A
B
C
图1--4
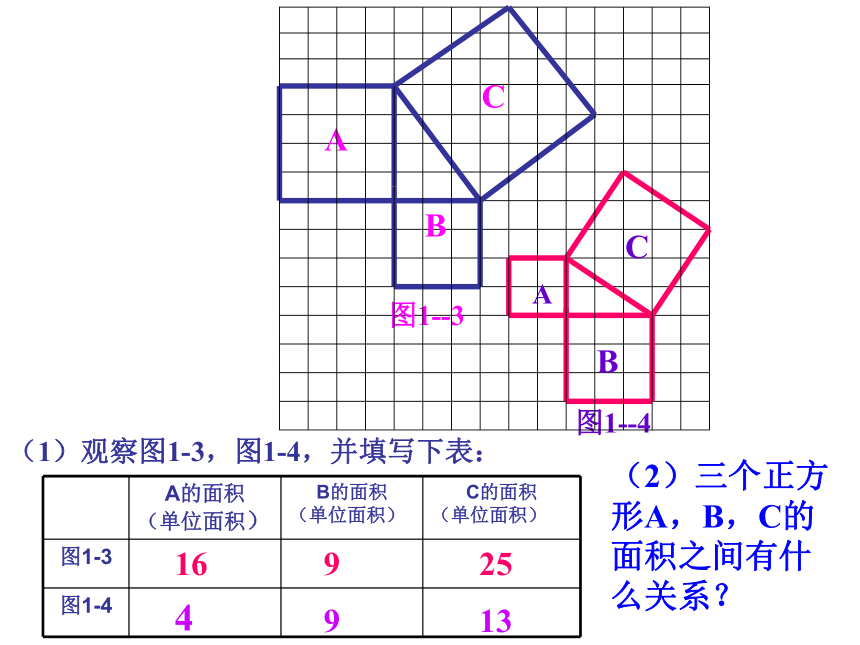
(1)观察图1-3,图1-4,并填写下表:
A的面积 (单位面积) B的面积 (单位面积) C的面积
(单位面积)
图1-3
图1-4
16
9
25
(2)三个正方形A,B,C的面积之间有什么关系?
4
9
13
P
Q
R
∵SP=9,SQ=14
SR=25
∴SP+SQ=SR
问题 这三个正方形的面积之间有什么关系?
P
Q
R
a
c
b
如果直角三角形的直角边分别是a、b,斜边是c ,观察等式,你有什么发现?
a2
b2
c2
SP + SQ = SR
a2 + b2 = c2
勾股定理(毕达哥拉斯定理)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
A
C
B
数学符号语言:
∵在Rt△ABC中, ∠C=90o
∴AC2+BC2=AB2或a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
小贴士
勾股史话
我国是最早了解勾股定理的国家之一.早在三千
多年前,周朝的数学家商高就提出,将一根直尺折成
一个直角,如果勾等于三,股等于四,那么弦就等于
五,即“勾三、股四、弦五”.它被记载于我国古代
著名的数学著作《周髀算经》中.在这本书中的另一
处,还记载了勾股定理的一般形式.这一发现,至少
早于古希腊人500多年.作为一名中国人,我们应为我
国古人的博学和多思而感到自豪!
勾股定理是人类文明的成果,几乎所有拥有古代文化的民族和国家都对勾股定理有所研究.在地球以外是否存在生命这个问题上,我国数学家华罗庚曾认为,如果外星人也拥有文明的话,我们可以用“勾股定理”的图形,作为人类探寻“外星人”并与“外星人”联系的“语言”.
请你求出图中字母所代表的正方形的面积:
X
81
144
⑴
169
144
Y
⑵
625
576
Z
⑶
X=225
Y=25
Z=49
求下列直角三角形中未知边的长:
8
x
17
解:在直角三角形中,
由勾股定理可得:
52+ 122= x2
即:x2=52+122
x2=169
∵x>0
∴x=13
16
20
x
12
5
x
解:在直角三角形中,
由勾股定理可得:
x2+ 162= 202
即:x2=202-162
x2=144
∵x>0
∴ x=12
解:在直角三角形中,
由勾股定理可得:
82+ x2= 172
即:x2=172-82
x2=225
∵x>0
∴x=15
A
C
B
A
C
C
B
B
A
那么正方形E和F的面积的和为 .
6cm
E
F
M
E
D
C
B
A
如图,所有的三角形均为直角三角形,所有的四边形均为正方形,且正方形M的边长为6cm,
36cm2
1、这节课你学到了什么知识?
2、运用“勾股定理”应注意什么问题?
3米
4米
台风袭击中,一棵大树在离地面3米处断裂,树的顶部落在离树根底部4米处。这棵树原来有多高?
B
A
c
1、在△ ABC中, ∠C=90°,
(1)若a=5,b=12,则c=__________.
(2)若a=15,c=25,则b=__________.
(3)若c=61,b=60,则a=_________.
(4)若a:b=3:4,c=10,则a=________,
b=________.
13
20
11
6
8
2、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
5
4
3
A
C
B
4
3
C
A
B
或
如图,在△ABC中 ∠ACB=90°,
AB=5cm,BC=3cm,CD⊥AB,垂足为D。
求:(1)AC的长;
(2)△ABC的面积;
(3)CD的长。
你能求出图中X的值吗?
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
∴售货员没搞错
∵
荧屏对角线大约为74厘米
《九章算术》中的引葭(jiā) 赴岸问题:
“今有池方一丈,葭(jiā)生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.”
题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.问水深和芦苇长各多少?
E
A
D
B′
B
C
做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.
3.1勾股定理
相传2500年前,毕达哥拉斯应邀出席宴会,宴会厅中铺着美丽的等腰直角三角形地砖,这位善于观察的数学家从看似平淡无奇的现象中发现了“神奇而伟大的定理”。
这是1955年希腊曾经发行的纪念一位数学家的邮票。
让我们一起回到2500年前,跟随毕达哥拉斯一起看看这等腰直角三角形的地砖铺成的地面:
A
B
C
问题
①地砖上有哪些常见的图形?
②图形之间有什么联系?
A
B
C
问题
①正方形A、B、C的面积跟等腰直角三角形的边长之间有什么关系?
②大胆猜想直角三角形三边之间的数量关系.
要求
①以直角三角形的三边为边长向外作正方形;
②计算出这三个正方形的面积。
P
Q
R
A
B
C
(每个网格均为正方形,
面积为1个平方单位)
P
Q
C
R
求正方形R的面积?
用“补”的方法
P
Q
C
R
用“割”的方法
Q
SR
SR
P
Q
R
∵SP=9,SQ=14
SR=25
∴SP+SQ=SR
问题 这三个正方形的面积之间有什么关系?
S1 S2 S3
在方格纸上任意画一个顶点都在格点上的直角三角形,并分别以这个三角形的三边向外作正方形,仿照上面方法求其面积,你又发现了什么?
A
B
C
图1--3
A
B
C
图1--4
(1)观察图1-3,图1-4,并填写下表:
A的面积 (单位面积) B的面积 (单位面积) C的面积
(单位面积)
图1-3
图1-4
16
9
25
(2)三个正方形A,B,C的面积之间有什么关系?
4
9
13
P
Q
R
∵SP=9,SQ=14
SR=25
∴SP+SQ=SR
问题 这三个正方形的面积之间有什么关系?
P
Q
R
a
c
b
如果直角三角形的直角边分别是a、b,斜边是c ,观察等式,你有什么发现?
a2
b2
c2
SP + SQ = SR
a2 + b2 = c2
勾股定理(毕达哥拉斯定理)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
A
C
B
数学符号语言:
∵在Rt△ABC中, ∠C=90o
∴AC2+BC2=AB2或a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
小贴士
勾股史话
我国是最早了解勾股定理的国家之一.早在三千
多年前,周朝的数学家商高就提出,将一根直尺折成
一个直角,如果勾等于三,股等于四,那么弦就等于
五,即“勾三、股四、弦五”.它被记载于我国古代
著名的数学著作《周髀算经》中.在这本书中的另一
处,还记载了勾股定理的一般形式.这一发现,至少
早于古希腊人500多年.作为一名中国人,我们应为我
国古人的博学和多思而感到自豪!
勾股定理是人类文明的成果,几乎所有拥有古代文化的民族和国家都对勾股定理有所研究.在地球以外是否存在生命这个问题上,我国数学家华罗庚曾认为,如果外星人也拥有文明的话,我们可以用“勾股定理”的图形,作为人类探寻“外星人”并与“外星人”联系的“语言”.
请你求出图中字母所代表的正方形的面积:
X
81
144
⑴
169
144
Y
⑵
625
576
Z
⑶
X=225
Y=25
Z=49
求下列直角三角形中未知边的长:
8
x
17
解:在直角三角形中,
由勾股定理可得:
52+ 122= x2
即:x2=52+122
x2=169
∵x>0
∴x=13
16
20
x
12
5
x
解:在直角三角形中,
由勾股定理可得:
x2+ 162= 202
即:x2=202-162
x2=144
∵x>0
∴ x=12
解:在直角三角形中,
由勾股定理可得:
82+ x2= 172
即:x2=172-82
x2=225
∵x>0
∴x=15
A
C
B
A
C
C
B
B
A
那么正方形E和F的面积的和为 .
6cm
E
F
M
E
D
C
B
A
如图,所有的三角形均为直角三角形,所有的四边形均为正方形,且正方形M的边长为6cm,
36cm2
1、这节课你学到了什么知识?
2、运用“勾股定理”应注意什么问题?
3米
4米
台风袭击中,一棵大树在离地面3米处断裂,树的顶部落在离树根底部4米处。这棵树原来有多高?
B
A
c
1、在△ ABC中, ∠C=90°,
(1)若a=5,b=12,则c=__________.
(2)若a=15,c=25,则b=__________.
(3)若c=61,b=60,则a=_________.
(4)若a:b=3:4,c=10,则a=________,
b=________.
13
20
11
6
8
2、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
5
4
3
A
C
B
4
3
C
A
B
或
如图,在△ABC中 ∠ACB=90°,
AB=5cm,BC=3cm,CD⊥AB,垂足为D。
求:(1)AC的长;
(2)△ABC的面积;
(3)CD的长。
你能求出图中X的值吗?
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
∴售货员没搞错
∵
荧屏对角线大约为74厘米
《九章算术》中的引葭(jiā) 赴岸问题:
“今有池方一丈,葭(jiā)生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.”
题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.问水深和芦苇长各多少?
E
A
D
B′
B
C
做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
