13.5.3 角平分线课件(20张ppt)
文档属性
| 名称 | 13.5.3 角平分线课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1009.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 16:10:39 | ||
图片预览






文档简介
(共20张PPT)
13.5.3角平分线
华师大版 八年级上册
教学目标
1.掌握角平分线的性质定理与逆定理.
2.在探索问题过程中体会知识间的相互联系,能够进行有条理的思考,并进行简单的推理。
【教学重点】角平分线的性质定理与逆定理.
【教学难点】角平分线的性质定理与逆定理的运用.
新知导入
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
(对折)
新知讲解
探究角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
(2)猜想:角的平分线上的点到角的两边的距离相等.
新知讲解
A
O
B
C
P
D
E
已知:如图,OC是∠AOB 的平分线,点P是OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为D和点E.
求证:PD = PE.
证明:∵OC平分∠ AOB
∴ ∠EOP= ∠DOP
∵PD⊥OA,PE⊥OB
∴ ∠PDO= ∠PEO=90°
在△PDO 和 △PEO中
∠EOP=∠DOP, ∠PDO=∠PEO,OP=OP
∴ △PDO≌△PEO(A.A.S.)
∴ PD=PE
新知讲解
A
O
B
C
P
D
E
角平分线上的点到角两边的距离相等.
符号语言:
∵ ∠1= ∠2, PD⊥OA, PE⊥OB
∴ PD=PE
知识点1、角平分线的性质定理
巩固练习
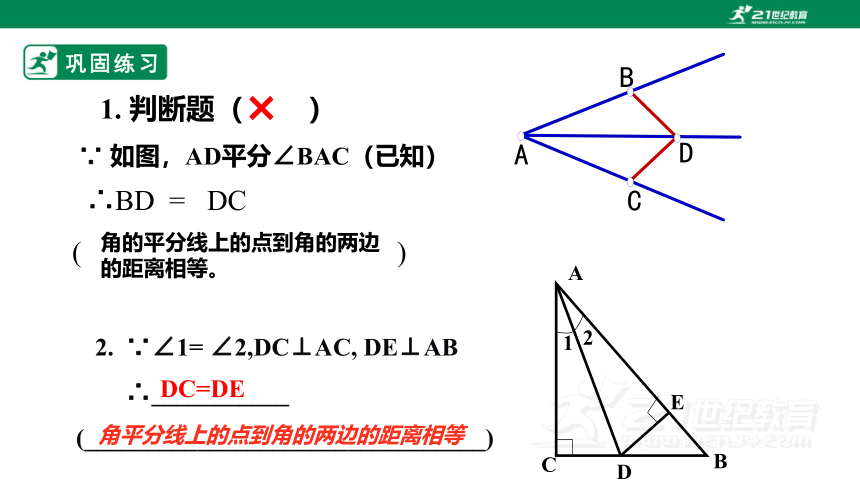
1. 判断题( )
∵ 如图,AD平分∠BAC(已知)
∴BD = DC
( )
角的平分线上的点到角的两边的距离相等。
×
2. ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(________________________________)
A
C
D
E
B
1
2
DC=DE
角平分线上的点到角的两边的距离相等
巩固练习
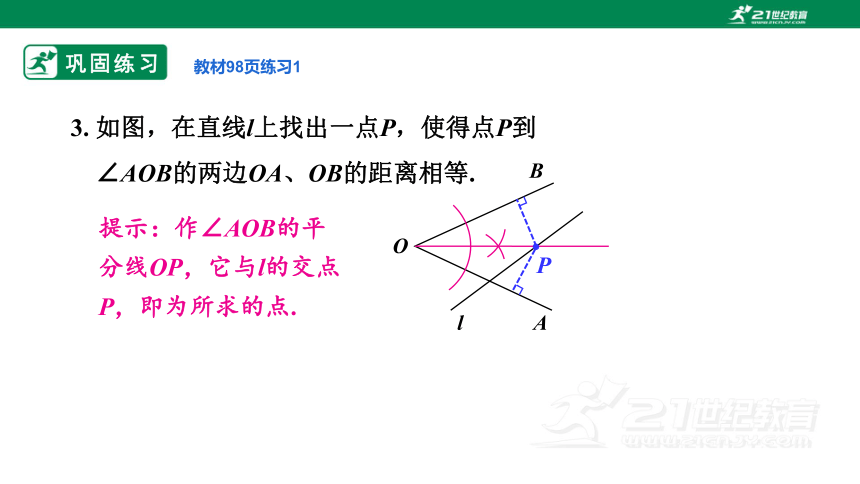
3. 如图,在直线l上找出一点P,使得点P到∠AOB的两边OA、OB的距离相等.
提示:作∠AOB的平分线OP,它与l的交点P,即为所求的点.
A
B
O
l
P
教材98页练习1
巩固练习
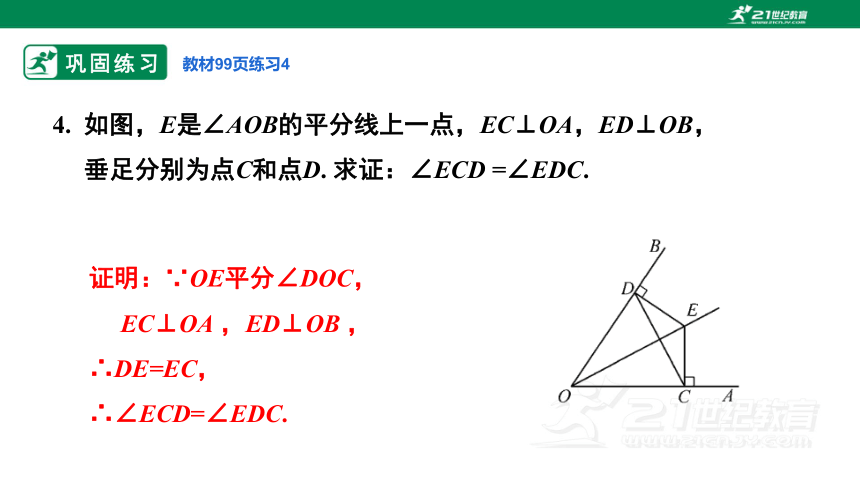
4. 如图,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为点C和点D. 求证:∠ECD =∠EDC.
证明:∵OE平分∠DOC,EC⊥OA ,ED⊥OB ,
∴DE=EC,
∴∠ECD=∠EDC.
教材99页练习4
新知讲解
这一定理描述了角平分线的性质,那么反过来会有什么结果呢?
条件 结论
性质定理
逆命题
一直线是一角的平分线
该直线上的点到角两边的距离相等
点到角两边的距离相等
该点在线段的角平分线上
逆命题是否是一个真命题?
新知讲解
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
证明:过点O、Q作射线OQ.
∵OQ⊥OA,QE⊥OB,
∴∠QDO=∠QEO=90°
在Rt△QDO和Rt△QEO中,
A
O
B
Q
D
E
∴点Q在∠AOB的平分线上.
∵OQ=OQ,QD=QE,
∴Rt△QDO≌Rt△QEO(H.L.)
∴∠DOQ=∠EOQ
新知讲解
角的内部到角两边距离相等的点在角的平分线上.
角平分线的性质定理与判定定理互为逆定理
A
O
B
Q
D
E
知识点2、角平分线的判定定理
新知讲解
如何证明“三角形三条边的角平分线交于一点”?
只需证明其中两条角平分线的交点一定在第三条角平分线上就可以了.
A
B
C
F
I
D
G
E
H
O
新知讲解
AO是∠BAC的平分线
BO是∠ABC的平分线
OI=OH
OG=OI
OG=OH
点O在∠BCA的平分线上
试试看,现在你会证明了吗?
A
B
C
F
I
D
G
E
H
O
巩固练习
5.如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F. 求证:点F在∠DAE的平分线上.
A
B
C
D
E
F
证明:作FG⊥AC,FH⊥BC,FM⊥AB﹐垂足分别为G、H 、M .
G
H
M
∵ CF平分∠ECB,BF平分∠CBD
∴ FG=FH=FM
∴点F在∠DAE的平分线上.
教材98页练习2
新知讲解
6. 如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF. 求证:点F在∠BAC的平分线上.
证明:∵BD⊥AC,CE⊥AB,
∴∠CDF=∠BEF=90 °.
在△CDF和△BEF中,
∵∠CDF=∠BEF=90 °,∠CFD=∠BFE,BF=CF,
∴△CDF≌△BEF( A.A.S.),
∴DF=EF,
∴点F在∠BAC的平分线上.
A
B
C
D
F
E
教材99页习题5
课堂总结
这节课我们学到了什么?
①掌握了角平分线的性质定理及其逆定理.
②利用角平分线性质定理证明两条线段相等.
拓展提高
A
C
B
E
D
P
M
H
K
如图,在△ABC的 顶点 B的外角的平分线BD与顶点 C的外角的平分线CE相交于点P.求证:点P到三边AB、BC、AC的距离相等.
证明:过点P作PM、PK、 PH分别垂直于AB、BC、AC,垂足为M、K、H。
∵BD平分∠CBM
∴PK=PM
同理PK=PH
∴PK=PM=PH
即点P到三边AB、BC、AC的距离相等
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.5.3角平分线
华师大版 八年级上册
教学目标
1.掌握角平分线的性质定理与逆定理.
2.在探索问题过程中体会知识间的相互联系,能够进行有条理的思考,并进行简单的推理。
【教学重点】角平分线的性质定理与逆定理.
【教学难点】角平分线的性质定理与逆定理的运用.
新知导入
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
(对折)
新知讲解
探究角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
(2)猜想:角的平分线上的点到角的两边的距离相等.
新知讲解
A
O
B
C
P
D
E
已知:如图,OC是∠AOB 的平分线,点P是OC上的任意一点,PD⊥OA,PE⊥OB,垂足分别为D和点E.
求证:PD = PE.
证明:∵OC平分∠ AOB
∴ ∠EOP= ∠DOP
∵PD⊥OA,PE⊥OB
∴ ∠PDO= ∠PEO=90°
在△PDO 和 △PEO中
∠EOP=∠DOP, ∠PDO=∠PEO,OP=OP
∴ △PDO≌△PEO(A.A.S.)
∴ PD=PE
新知讲解
A
O
B
C
P
D
E
角平分线上的点到角两边的距离相等.
符号语言:
∵ ∠1= ∠2, PD⊥OA, PE⊥OB
∴ PD=PE
知识点1、角平分线的性质定理
巩固练习
1. 判断题( )
∵ 如图,AD平分∠BAC(已知)
∴BD = DC
( )
角的平分线上的点到角的两边的距离相等。
×
2. ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(________________________________)
A
C
D
E
B
1
2
DC=DE
角平分线上的点到角的两边的距离相等
巩固练习
3. 如图,在直线l上找出一点P,使得点P到∠AOB的两边OA、OB的距离相等.
提示:作∠AOB的平分线OP,它与l的交点P,即为所求的点.
A
B
O
l
P
教材98页练习1
巩固练习
4. 如图,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为点C和点D. 求证:∠ECD =∠EDC.
证明:∵OE平分∠DOC,EC⊥OA ,ED⊥OB ,
∴DE=EC,
∴∠ECD=∠EDC.
教材99页练习4
新知讲解
这一定理描述了角平分线的性质,那么反过来会有什么结果呢?
条件 结论
性质定理
逆命题
一直线是一角的平分线
该直线上的点到角两边的距离相等
点到角两边的距离相等
该点在线段的角平分线上
逆命题是否是一个真命题?
新知讲解
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
证明:过点O、Q作射线OQ.
∵OQ⊥OA,QE⊥OB,
∴∠QDO=∠QEO=90°
在Rt△QDO和Rt△QEO中,
A
O
B
Q
D
E
∴点Q在∠AOB的平分线上.
∵OQ=OQ,QD=QE,
∴Rt△QDO≌Rt△QEO(H.L.)
∴∠DOQ=∠EOQ
新知讲解
角的内部到角两边距离相等的点在角的平分线上.
角平分线的性质定理与判定定理互为逆定理
A
O
B
Q
D
E
知识点2、角平分线的判定定理
新知讲解
如何证明“三角形三条边的角平分线交于一点”?
只需证明其中两条角平分线的交点一定在第三条角平分线上就可以了.
A
B
C
F
I
D
G
E
H
O
新知讲解
AO是∠BAC的平分线
BO是∠ABC的平分线
OI=OH
OG=OI
OG=OH
点O在∠BCA的平分线上
试试看,现在你会证明了吗?
A
B
C
F
I
D
G
E
H
O
巩固练习
5.如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F. 求证:点F在∠DAE的平分线上.
A
B
C
D
E
F
证明:作FG⊥AC,FH⊥BC,FM⊥AB﹐垂足分别为G、H 、M .
G
H
M
∵ CF平分∠ECB,BF平分∠CBD
∴ FG=FH=FM
∴点F在∠DAE的平分线上.
教材98页练习2
新知讲解
6. 如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF. 求证:点F在∠BAC的平分线上.
证明:∵BD⊥AC,CE⊥AB,
∴∠CDF=∠BEF=90 °.
在△CDF和△BEF中,
∵∠CDF=∠BEF=90 °,∠CFD=∠BFE,BF=CF,
∴△CDF≌△BEF( A.A.S.),
∴DF=EF,
∴点F在∠BAC的平分线上.
A
B
C
D
F
E
教材99页习题5
课堂总结
这节课我们学到了什么?
①掌握了角平分线的性质定理及其逆定理.
②利用角平分线性质定理证明两条线段相等.
拓展提高
A
C
B
E
D
P
M
H
K
如图,在△ABC的 顶点 B的外角的平分线BD与顶点 C的外角的平分线CE相交于点P.求证:点P到三边AB、BC、AC的距离相等.
证明:过点P作PM、PK、 PH分别垂直于AB、BC、AC,垂足为M、K、H。
∵BD平分∠CBM
∴PK=PM
同理PK=PH
∴PK=PM=PH
即点P到三边AB、BC、AC的距离相等
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
