人教版七年级上册 第三章 一元一次方程小结 课件(共25张PPT)
文档属性
| 名称 | 人教版七年级上册 第三章 一元一次方程小结 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 474.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
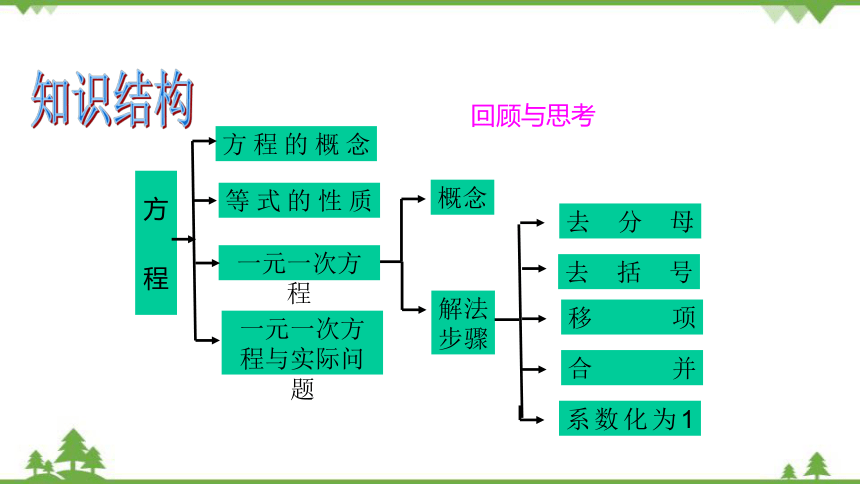
一元一次方程复习(一)
回顾与思考
方 程
概念
解法步骤
去括号
移项
合并
去分母
系数化为1
等式的性质
方程的概念
一元一次方程
一元一次方程与实际问题
1、什么叫方程?
含有未知数的等式叫做方程.
注意:
判断一个式子是不是方程,要看两点:
一是等式;二是含有未知数。二者缺一不可.
知识点复习一:
1、方程的概念
2、一元一次方程的定义
3、方程的解
2.什么是一元一次方程?
想一想
只有一个未知数
一元一次方程 未知数的次数为1
分母不含有字母
3、方程的解:
使方程中等号左右两边相等的未知数的值
1.下列各式中,是方程的是( )
A. x + 3 B. x – 2 > 0
C.2x + 7 = 3 D.2 + 3 = 5
c
2
1
2.在下列方程中哪些是一元一次方程( )
(1)3x+5=12; (2) + =5; (3)2x+y=3;
(4)y2+5y-6=0; (5) = 2.
练习一
C
(1)、(2)
4、 若 是一元一次方程,
3、写一个解为 的一元一次方程
是 。
X+2=0
2
求方程的解的过程叫解方程.
知识点复习二:
解方程:
2、若x=-3是方程x+a=4的解,则a的值是 .
1、方程x+8=4的解是 .
练习二
7
X= - 4
等式性质有哪些?并以字母的形式表示出来
等式性质1:
如果a=b ,那么a+c=b+c
需注意的是“同一个数,或同一个式子”。
知识点复习三:等式的性质
等式性质2:
如果a=b , 那么ac=bc
如果a=b , 那么a/c=b/c
需注意的是“两边都乘,不要漏乘”;“同除一个非0的数”
1、大家判断一下,下列方程的变形是否正确?
(1)
(2)
(3)
(4)
知识点练习三
( )
( )
( )
( )
×
×
×
√
3、已知 x = y,下列变形中不一定正确的是( )
A.x-5=y-5 B.-3x=-3y
C.mx=my D.
2、若a+2b = x + 10,则2a + 2b = x + 10+ .
a
D
注意变号,防止漏乘;
移项要变号,
知识点复习四:解一元一次方程
(2)
知识点练习四
解方程:
(1)
(3)
知识点复习五:列方程解应用题
A.B两地间相距360km,甲车从A地出发往B地,每小时行72km,甲车出发15分钟后,乙车从B地出发开往A地,每小时行48km,甲车出发后行驶多少小时后,两车相遇
知识点练习五
(改为问:乙车出发后行驶多少小时后,两车相遇 )
(如果问:甲车出发后行驶多少小时后,两车相距132km )
解:设甲车出发后行驶X小时后两车相遇,由题意得。
解之得
X=3.1
答:甲车出发后行驶3.1小时后两车相遇。
四 应用题
1、元旦某公园的成人的门票每张8元,儿童门票半价(即每张4元),全天共售出门票3000张,收入15600元。问这天售出儿童门票多少张?
解:设售出儿童门票x张
根据题意,得:
解方程,得: x = 2100
答:共售出儿童票2100张
2、某部队开展支农活动,甲队27人,乙队19人,现另调26人去支援,使甲队是乙队的2倍,问应调往甲队、乙队各多少人?
解:设调往甲队x人,则调往乙队(26-x)人
根据题意,得方程:
解方程得:x = 21
答:调往甲队21人。调往乙队5人。
综合训练
思考题:某商场共出售甲、乙两种商品共50件,该50件商品总进价108000元,其中商品甲每件进价1800元,出售后获利200元;商品乙每件进价2400元,出售后获利300元。问该商场出售这50件商品共获利是多少元?
解:设出售甲种商品X件,则乙种商品(50-X)件,由题意得。
解之得
X=20
答:商场出售这50件商品共获利13000元。
∴ 50-X=30
∴ 50件共获利=20 × 200+30 × 300=13000
1.一元一次方程及其有关概念
2.等式的两个性质及其应用。
3.解一元一次方程及其应用。
课堂小结
一元一次方程复习(一)
回顾与思考
方 程
概念
解法步骤
去括号
移项
合并
去分母
系数化为1
等式的性质
方程的概念
一元一次方程
一元一次方程与实际问题
1、什么叫方程?
含有未知数的等式叫做方程.
注意:
判断一个式子是不是方程,要看两点:
一是等式;二是含有未知数。二者缺一不可.
知识点复习一:
1、方程的概念
2、一元一次方程的定义
3、方程的解
2.什么是一元一次方程?
想一想
只有一个未知数
一元一次方程 未知数的次数为1
分母不含有字母
3、方程的解:
使方程中等号左右两边相等的未知数的值
1.下列各式中,是方程的是( )
A. x + 3 B. x – 2 > 0
C.2x + 7 = 3 D.2 + 3 = 5
c
2
1
2.在下列方程中哪些是一元一次方程( )
(1)3x+5=12; (2) + =5; (3)2x+y=3;
(4)y2+5y-6=0; (5) = 2.
练习一
C
(1)、(2)
4、 若 是一元一次方程,
3、写一个解为 的一元一次方程
是 。
X+2=0
2
求方程的解的过程叫解方程.
知识点复习二:
解方程:
2、若x=-3是方程x+a=4的解,则a的值是 .
1、方程x+8=4的解是 .
练习二
7
X= - 4
等式性质有哪些?并以字母的形式表示出来
等式性质1:
如果a=b ,那么a+c=b+c
需注意的是“同一个数,或同一个式子”。
知识点复习三:等式的性质
等式性质2:
如果a=b , 那么ac=bc
如果a=b , 那么a/c=b/c
需注意的是“两边都乘,不要漏乘”;“同除一个非0的数”
1、大家判断一下,下列方程的变形是否正确?
(1)
(2)
(3)
(4)
知识点练习三
( )
( )
( )
( )
×
×
×
√
3、已知 x = y,下列变形中不一定正确的是( )
A.x-5=y-5 B.-3x=-3y
C.mx=my D.
2、若a+2b = x + 10,则2a + 2b = x + 10+ .
a
D
注意变号,防止漏乘;
移项要变号,
知识点复习四:解一元一次方程
(2)
知识点练习四
解方程:
(1)
(3)
知识点复习五:列方程解应用题
A.B两地间相距360km,甲车从A地出发往B地,每小时行72km,甲车出发15分钟后,乙车从B地出发开往A地,每小时行48km,甲车出发后行驶多少小时后,两车相遇
知识点练习五
(改为问:乙车出发后行驶多少小时后,两车相遇 )
(如果问:甲车出发后行驶多少小时后,两车相距132km )
解:设甲车出发后行驶X小时后两车相遇,由题意得。
解之得
X=3.1
答:甲车出发后行驶3.1小时后两车相遇。
四 应用题
1、元旦某公园的成人的门票每张8元,儿童门票半价(即每张4元),全天共售出门票3000张,收入15600元。问这天售出儿童门票多少张?
解:设售出儿童门票x张
根据题意,得:
解方程,得: x = 2100
答:共售出儿童票2100张
2、某部队开展支农活动,甲队27人,乙队19人,现另调26人去支援,使甲队是乙队的2倍,问应调往甲队、乙队各多少人?
解:设调往甲队x人,则调往乙队(26-x)人
根据题意,得方程:
解方程得:x = 21
答:调往甲队21人。调往乙队5人。
综合训练
思考题:某商场共出售甲、乙两种商品共50件,该50件商品总进价108000元,其中商品甲每件进价1800元,出售后获利200元;商品乙每件进价2400元,出售后获利300元。问该商场出售这50件商品共获利是多少元?
解:设出售甲种商品X件,则乙种商品(50-X)件,由题意得。
解之得
X=20
答:商场出售这50件商品共获利13000元。
∴ 50-X=30
∴ 50件共获利=20 × 200+30 × 300=13000
1.一元一次方程及其有关概念
2.等式的两个性质及其应用。
3.解一元一次方程及其应用。
课堂小结
