苏科版七年级上册2.2 有理数与无理数(共23张PPT)
文档属性
| 名称 | 苏科版七年级上册2.2 有理数与无理数(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 464.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 07:10:40 | ||
图片预览







文档简介
(共23张PPT)
有理数的有关概念
一、正数和负数
名称
类型
正数
负数
概 念
数的符号
与0的关系
⑵0是一个介于正数和负数之间的数,即它是正数与负数的分界点,是分类的基准。
像8 844.43、100、357、78 这样的数是正数
像-154、-38.87、-117.3、-0.102%这样的数是负数
“+"读作"正"、如“+3"读作"正 3".一般情况下正数前的“+"省略不写
“-”读作“负”,如“-9”读作“负9”.负数前的“-"一定要写,不可以省略
⑴0既不是正数,也不是负数;
用正数和负数可以表示具有相反意义的量
表示相反意义的两个量中,如果其中的一个量用正数表示,那么另一个量就用负数表示.
在现实生活中,如果零上、上升、向东、前进、收入、高于海平面、节约、盈利、买进等意义的量规定为正,那么把与这些量具有相反意义的零下、下降、向西、后退、支出、低于海平面、浪费、亏损、卖出等意义的量规定为负。
特别说明:在一对相反意义的量中,哪种意义为正是可以任意选择的.例如可以规定下降为正,则和它具有相反意义的上升就为负.若题目中没有特别的说明,则应遵循生活习惯.
典型例题
例1 ⑴如果收入10元记作+10元,那么支出10元记作( )
A.+20元 B.+10元 C.-10元 D.-20元
⑵古代数学家刘徽在注解《九章算术》时,写有“今两算得失相反,要令正负以名之”,意思是今有两数若其意义相反,则分别叫做正数与负数. 若气温为零上10 ℃记作+10 ℃,则-3℃表示气温为( )
A.零上3℃ B.零下3℃ C.零上7℃ D. 零下7℃
⑶向指定方向变化用正数表示,向指定方向的相反方向变化用负数表示,“体重减少1.5kg”换一种说法可以叙述为“体重增加______kg”
C
B
-1.5
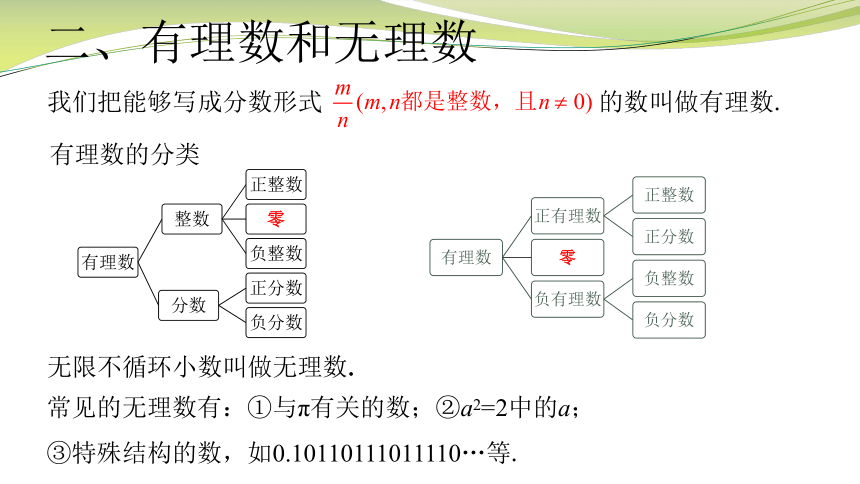
二、有理数和无理数
我们把能够写成分数形式 的数叫做有理数.
有理数的分类
无限不循环小数叫做无理数.
常见的无理数有:①与π有关的数;②a2=2中的a;
③特殊结构的数,如0.10110111011110…等.
典型例题
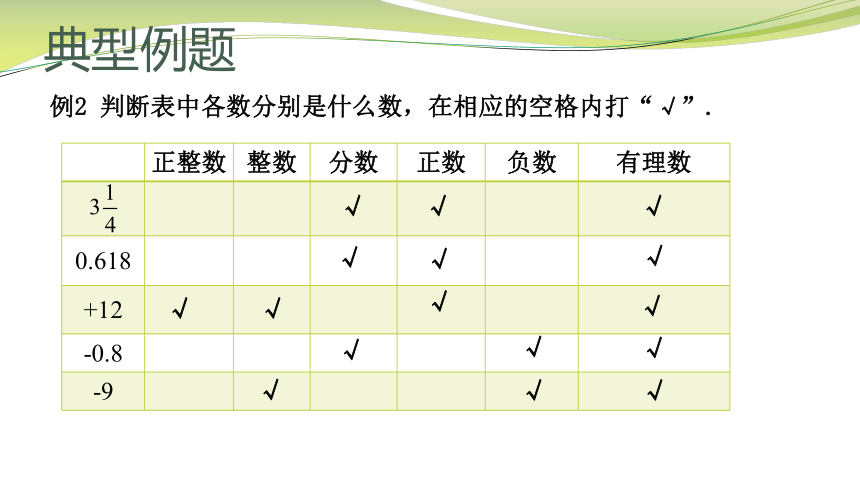
正整数 整数 分数 正数 负数 有理数
0.618
+12
-0.8
-9
例2 判断表中各数分别是什么数,在相应的空格内打“√”.
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
典型例题
例3 将下列各数填入相应的括号内
正数集合:{ …}
负数集合:{ …}
负有理数集合:{ …}
非负有理数集合:{ …}
6个“非” 的理解
非正有理数:
非负有理数:
非正整数:
非负整数:
非正数:
非负数:
0+负有理数
0+正有理数
0+负整数
0+正整数
0+负数
0+正数
典型例题
例4 填空:
最小的正整数是__________,
是负数而不是分数的有理数是__________,
是整数而不是正数的有理数是__________,
既不是正数也不是负数的有理数是__________.
1
负整数
非正整数
0
像这样规定了原点、正方向和单位长度的直线叫数轴。
0
1
2
3
4
-4
-1
-2
-3
三、数轴
-1
-2
-3
1
2
-4
-1
-2
-3
1
2
3
0
4
-4
-3
-2
1
2
3
0
4
0
-1
1
2
-5
-10
-15
5
10
15
0
1
2
3
4
5
没有原点
没有正方向,不是直线
数字没有保持从左往右
依次递增
单位长度不统一
例5 判断以下直线是否为数轴
例6 在数轴上表示下列各数:0,1,-5,2.5,-0.8,-2,4,并将这些数按从小到大的顺序排列(用“<”连接)
-1
-2
-3
1
2
3
0
4
5
-4
-5
0
-5
2.5
4
-0.8
-5< < -0.8<0< <2.5<4
数轴上的数,右大左小
正数>0,负数<0,正数>负数
例7 小李不慎将墨水滴在数轴上,根据图中的数值,判断墨迹盖住的整数有______个?
列举法:-5,-4,-3,0,1,2
6
整数点覆盖问题
变式 数轴上表示整数的点称为整点。某数轴的单位长度是1cm,若在这个数轴上随意画出一条长为4cm的线段AB,则线段AB盖住的整点个数
为( )
A.3 B.4 C.3或4 D.4或5
线段AB
5个
4个
5个
D
0
1
2
3
4
-1
5
6
0
1
2
3
4
-1
5
6
0
1
2
3
4
-1
5
6
变式 长为2.5个单位长度的木条放在数轴上,最少能覆盖_____个表示整数的点,最多能覆盖_____个表示整数的点
3个
2个
3个
2
3
0
1
2
3
4
-1
5
6
0
1
2
3
4
-1
5
6
0
1
2
3
4
-1
5
6
例8 (1)在数轴上把表示2的点向右移动5个单位长度,所得的对应点是( )
A.7 B.-3 C.6 D.8
(2)一只蚂蚁从数轴上的点A出发爬了6个单位长度到了原点,则点A所表示的数是( )
A.6 B.-6 C.±6 D.±9
(3)数轴上一动点A向左移动3个单位长度到达点B,再向右移动6个单位长度到达点C,若C表示的数为3,则点A表示的数为( )
A.6 B.0 C.-6 D.-2
A
C
B
点的移动问题
四、绝对值与相反数
绝对值:数轴上表示一个数的点与原点的距离叫做这个数的绝对值,一个数a的绝对值记作 。
相反数:符号不同、绝对值相同(即只有符号不同)的两个数互为相反数,其中一个数叫做另一个数的相反数 。0的相反数是0。
数轴上,表示互为相反数(0除外)的两个点,位于原点的两侧,到原点的距离相等。
0
1
2
3
4
-4
-1
-2
-3
典型例题
例9 填空:
(1) 的绝对值是____; 的绝对值是____;0的绝对值是____.
(2)绝对值等于5的数是____;绝对值小于5的整数有____个,其中绝对值最小的整数是____.
(3)观察数轴:绝对值大于2且不大于7的整数
是 .
0
±5
9
0
±3,±4,±5,±6,±7
0
4
2
-2
-6
-4
-1
-3
-5
1
3
5
6
7
-7
(6)如图,图中数轴的单位长度为1,请回答下列问题:
①如果点A、B表示的数互为相反数,那么点C表示的数是_____.
②如果点E、B表示的数互为相反数,那么点D表示的数是_____.
例9 (4) 4的相反数是 ; 的相反数是 ;
-520的相反数是 .
(5) a的相反数是____;-a的相反数是 .
-4
520
-a
-(-a )
=a
0
0
-1
-5
绝对值的性质
如果a表示一个数,那么|a|=
绝对值的性质
文字描述
正数的绝对值是它本身
0的绝对值是0
负数的绝对值是它的相反数
用式子表示
a(a>0),
0(a=0),
-a(a<0)
因为我们把数轴上表示一个数的点到原点的距离看成这个数的绝对值的几何意义,因此,任意一个有理数的绝对值都是非负数.
相反数的性质
互为相反数的两个数,和为0.
若x与y互为相反数,则x+y=0(即x=-y).
若两个数的和为0,则这两个数互为相反数.
若x+y=0(即x=-y),则x与y互为相反数.
借2元,还2元,
不欠钱
典型例题
例10 若|a|+|b|=0,则a=____,b=____.
0
0
(1)|m|+|n-1|=0,则m=____,n=____.
0
1
(2)|m-2|+|n-5|=0,则m+n=____.
7
∵|m|+|n-1|=0
∴|m|=0,|n-1|=0
∴m=0,n-1=0
∵|m-2|+|n-5|=0
∴|m-2|=0,|n-5|=0
∴m-2=0,n-5=0
∴m=2,n=5
典型例题
例10 (3)若|m|=-|n|,则m与n满足的条件是 .
(4)|m-2|和|n-8|互为相反数,求m+n的值.
(3)|m|=-|n|,即|m|+|n|=0
(4)解:∵|m-2|和|n-8|互为相反数
∴|m-2|+|n-8|=0
∴|m-2|=0,|n-8|=0
∴m-2=0,n-8=0.
∴m=2,n=8 ∴m+n=10
m=n=0
谢 谢
有理数的有关概念
一、正数和负数
名称
类型
正数
负数
概 念
数的符号
与0的关系
⑵0是一个介于正数和负数之间的数,即它是正数与负数的分界点,是分类的基准。
像8 844.43、100、357、78 这样的数是正数
像-154、-38.87、-117.3、-0.102%这样的数是负数
“+"读作"正"、如“+3"读作"正 3".一般情况下正数前的“+"省略不写
“-”读作“负”,如“-9”读作“负9”.负数前的“-"一定要写,不可以省略
⑴0既不是正数,也不是负数;
用正数和负数可以表示具有相反意义的量
表示相反意义的两个量中,如果其中的一个量用正数表示,那么另一个量就用负数表示.
在现实生活中,如果零上、上升、向东、前进、收入、高于海平面、节约、盈利、买进等意义的量规定为正,那么把与这些量具有相反意义的零下、下降、向西、后退、支出、低于海平面、浪费、亏损、卖出等意义的量规定为负。
特别说明:在一对相反意义的量中,哪种意义为正是可以任意选择的.例如可以规定下降为正,则和它具有相反意义的上升就为负.若题目中没有特别的说明,则应遵循生活习惯.
典型例题
例1 ⑴如果收入10元记作+10元,那么支出10元记作( )
A.+20元 B.+10元 C.-10元 D.-20元
⑵古代数学家刘徽在注解《九章算术》时,写有“今两算得失相反,要令正负以名之”,意思是今有两数若其意义相反,则分别叫做正数与负数. 若气温为零上10 ℃记作+10 ℃,则-3℃表示气温为( )
A.零上3℃ B.零下3℃ C.零上7℃ D. 零下7℃
⑶向指定方向变化用正数表示,向指定方向的相反方向变化用负数表示,“体重减少1.5kg”换一种说法可以叙述为“体重增加______kg”
C
B
-1.5
二、有理数和无理数
我们把能够写成分数形式 的数叫做有理数.
有理数的分类
无限不循环小数叫做无理数.
常见的无理数有:①与π有关的数;②a2=2中的a;
③特殊结构的数,如0.10110111011110…等.
典型例题
正整数 整数 分数 正数 负数 有理数
0.618
+12
-0.8
-9
例2 判断表中各数分别是什么数,在相应的空格内打“√”.
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
典型例题
例3 将下列各数填入相应的括号内
正数集合:{ …}
负数集合:{ …}
负有理数集合:{ …}
非负有理数集合:{ …}
6个“非” 的理解
非正有理数:
非负有理数:
非正整数:
非负整数:
非正数:
非负数:
0+负有理数
0+正有理数
0+负整数
0+正整数
0+负数
0+正数
典型例题
例4 填空:
最小的正整数是__________,
是负数而不是分数的有理数是__________,
是整数而不是正数的有理数是__________,
既不是正数也不是负数的有理数是__________.
1
负整数
非正整数
0
像这样规定了原点、正方向和单位长度的直线叫数轴。
0
1
2
3
4
-4
-1
-2
-3
三、数轴
-1
-2
-3
1
2
-4
-1
-2
-3
1
2
3
0
4
-4
-3
-2
1
2
3
0
4
0
-1
1
2
-5
-10
-15
5
10
15
0
1
2
3
4
5
没有原点
没有正方向,不是直线
数字没有保持从左往右
依次递增
单位长度不统一
例5 判断以下直线是否为数轴
例6 在数轴上表示下列各数:0,1,-5,2.5,-0.8,-2,4,并将这些数按从小到大的顺序排列(用“<”连接)
-1
-2
-3
1
2
3
0
4
5
-4
-5
0
-5
2.5
4
-0.8
-5< < -0.8<0< <2.5<4
数轴上的数,右大左小
正数>0,负数<0,正数>负数
例7 小李不慎将墨水滴在数轴上,根据图中的数值,判断墨迹盖住的整数有______个?
列举法:-5,-4,-3,0,1,2
6
整数点覆盖问题
变式 数轴上表示整数的点称为整点。某数轴的单位长度是1cm,若在这个数轴上随意画出一条长为4cm的线段AB,则线段AB盖住的整点个数
为( )
A.3 B.4 C.3或4 D.4或5
线段AB
5个
4个
5个
D
0
1
2
3
4
-1
5
6
0
1
2
3
4
-1
5
6
0
1
2
3
4
-1
5
6
变式 长为2.5个单位长度的木条放在数轴上,最少能覆盖_____个表示整数的点,最多能覆盖_____个表示整数的点
3个
2个
3个
2
3
0
1
2
3
4
-1
5
6
0
1
2
3
4
-1
5
6
0
1
2
3
4
-1
5
6
例8 (1)在数轴上把表示2的点向右移动5个单位长度,所得的对应点是( )
A.7 B.-3 C.6 D.8
(2)一只蚂蚁从数轴上的点A出发爬了6个单位长度到了原点,则点A所表示的数是( )
A.6 B.-6 C.±6 D.±9
(3)数轴上一动点A向左移动3个单位长度到达点B,再向右移动6个单位长度到达点C,若C表示的数为3,则点A表示的数为( )
A.6 B.0 C.-6 D.-2
A
C
B
点的移动问题
四、绝对值与相反数
绝对值:数轴上表示一个数的点与原点的距离叫做这个数的绝对值,一个数a的绝对值记作 。
相反数:符号不同、绝对值相同(即只有符号不同)的两个数互为相反数,其中一个数叫做另一个数的相反数 。0的相反数是0。
数轴上,表示互为相反数(0除外)的两个点,位于原点的两侧,到原点的距离相等。
0
1
2
3
4
-4
-1
-2
-3
典型例题
例9 填空:
(1) 的绝对值是____; 的绝对值是____;0的绝对值是____.
(2)绝对值等于5的数是____;绝对值小于5的整数有____个,其中绝对值最小的整数是____.
(3)观察数轴:绝对值大于2且不大于7的整数
是 .
0
±5
9
0
±3,±4,±5,±6,±7
0
4
2
-2
-6
-4
-1
-3
-5
1
3
5
6
7
-7
(6)如图,图中数轴的单位长度为1,请回答下列问题:
①如果点A、B表示的数互为相反数,那么点C表示的数是_____.
②如果点E、B表示的数互为相反数,那么点D表示的数是_____.
例9 (4) 4的相反数是 ; 的相反数是 ;
-520的相反数是 .
(5) a的相反数是____;-a的相反数是 .
-4
520
-a
-(-a )
=a
0
0
-1
-5
绝对值的性质
如果a表示一个数,那么|a|=
绝对值的性质
文字描述
正数的绝对值是它本身
0的绝对值是0
负数的绝对值是它的相反数
用式子表示
a(a>0),
0(a=0),
-a(a<0)
因为我们把数轴上表示一个数的点到原点的距离看成这个数的绝对值的几何意义,因此,任意一个有理数的绝对值都是非负数.
相反数的性质
互为相反数的两个数,和为0.
若x与y互为相反数,则x+y=0(即x=-y).
若两个数的和为0,则这两个数互为相反数.
若x+y=0(即x=-y),则x与y互为相反数.
借2元,还2元,
不欠钱
典型例题
例10 若|a|+|b|=0,则a=____,b=____.
0
0
(1)|m|+|n-1|=0,则m=____,n=____.
0
1
(2)|m-2|+|n-5|=0,则m+n=____.
7
∵|m|+|n-1|=0
∴|m|=0,|n-1|=0
∴m=0,n-1=0
∵|m-2|+|n-5|=0
∴|m-2|=0,|n-5|=0
∴m-2=0,n-5=0
∴m=2,n=5
典型例题
例10 (3)若|m|=-|n|,则m与n满足的条件是 .
(4)|m-2|和|n-8|互为相反数,求m+n的值.
(3)|m|=-|n|,即|m|+|n|=0
(4)解:∵|m-2|和|n-8|互为相反数
∴|m-2|+|n-8|=0
∴|m-2|=0,|n-8|=0
∴m-2=0,n-8=0.
∴m=2,n=8 ∴m+n=10
m=n=0
谢 谢
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
