2022-2023学年人教版九年级数学上册第23章旋转 解答优生辅导训练题(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册第23章旋转 解答优生辅导训练题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 530.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 11:18:42 | ||
图片预览


文档简介
2022-2023学年人教版九年级数学上册《第23章旋转》解答优生辅导训练题(附答案)
1.如图,在△ABC中,∠B=45°,∠C=60°,将△ABC绕点A旋转30°后得到△AB1C1,求∠BAC1的度数.
2.如图①,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图②).
(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,求此时旋转角α的度数;
(3)如图③,在旋转过程中,设AC′与DE所在直线交于点P,当△ADP成为等腰三角形时,求此时的旋转角α的度数.(直接写出结果)
3.一副三角板如图1摆放,∠C=∠DFE=90°,∠B=30°,∠E=45°,点F在BC上,点A在DF上,且AF平分∠CAB,现将三角板DFE绕点F以每秒5°的速度顺时针旋转(当点D落在射线FB上时停止旋转),设旋转时间为t秒.
(1)当t= 秒时,DE∥AB;当t= 秒时,DE⊥AB;
(2)在旋转过程中,DF与AB的交点记为P,如图2,若△AFP有两个内角相等,求t的值;
(3)当边DE与边AB、BC分别交于点M、N时,如图3,连接AE,设∠BAE=x°,∠AED=y°,∠DFB=z°,试问x+y+z是否为定值?若是,请求出定值;若不是,请说明理由.
4.小志同学在玩一副直角三角尺时发现:含45°角的直角三角尺的斜边可与含30°角的直角三角尺的较长直角边完成重合(如图①),即△CD的顶点A′,C分别与△BAC的顶点A,C重合现在,他让△CDA固定不动,将△BAC通过变换使斜边BC经过△CDA的直角顶点D.
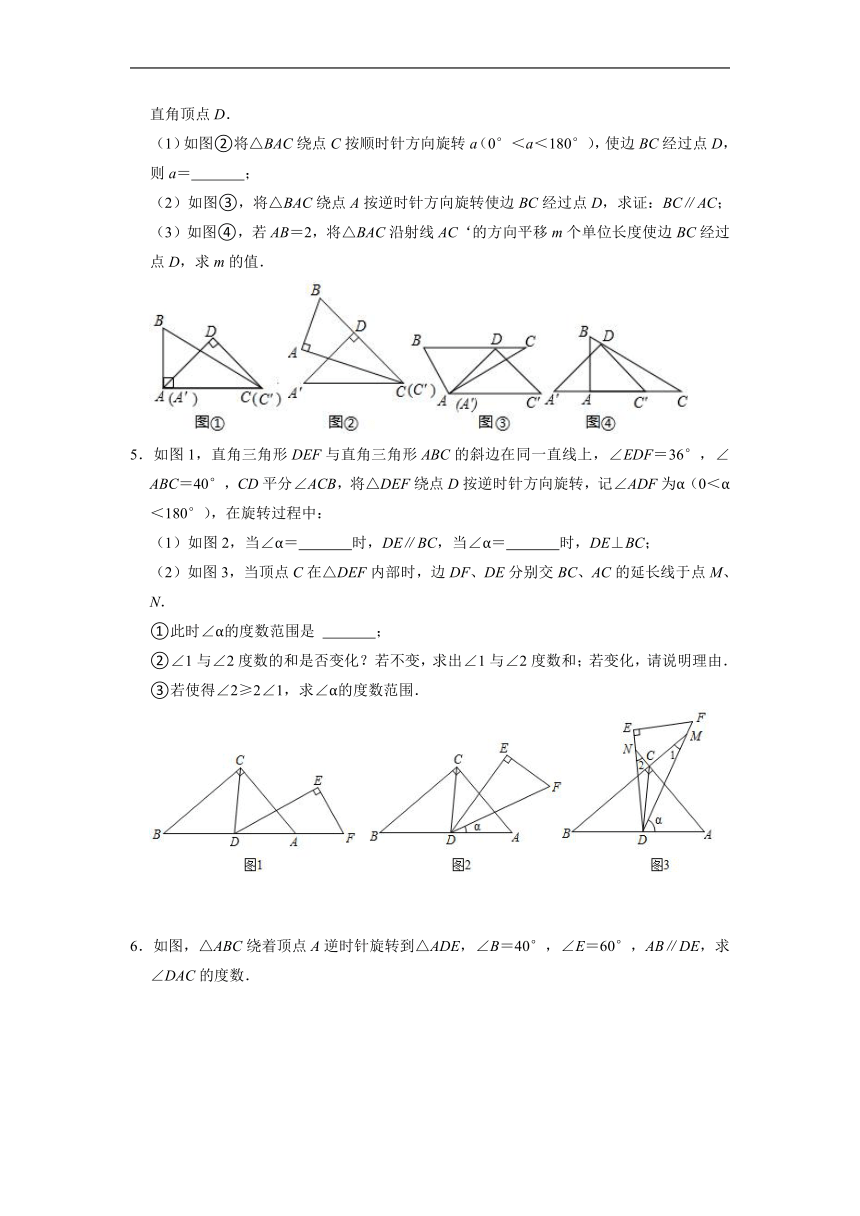
(1)如图②将△BAC绕点C按顺时针方向旋转a(0°<a<180°),使边BC经过点D,则a= ;
(2)如图③,将△BAC绕点A按逆时针方向旋转使边BC经过点D,求证:BC∥AC;
(3)如图④,若AB=2,将△BAC沿射线AC‘的方向平移m个单位长度使边BC经过点D,求m的值.
5.如图1,直角三角形DEF与直角三角形ABC的斜边在同一直线上,∠EDF=36°,∠ABC=40°,CD平分∠ACB,将△DEF绕点D按逆时针方向旋转,记∠ADF为α(0<α<180°),在旋转过程中:
(1)如图2,当∠α= 时,DE∥BC,当∠α= 时,DE⊥BC;
(2)如图3,当顶点C在△DEF内部时,边DF、DE分别交BC、AC的延长线于点M、N.
①此时∠α的度数范围是 ;
②∠1与∠2度数的和是否变化?若不变,求出∠1与∠2度数和;若变化,请说明理由.
③若使得∠2≥2∠1,求∠α的度数范围.
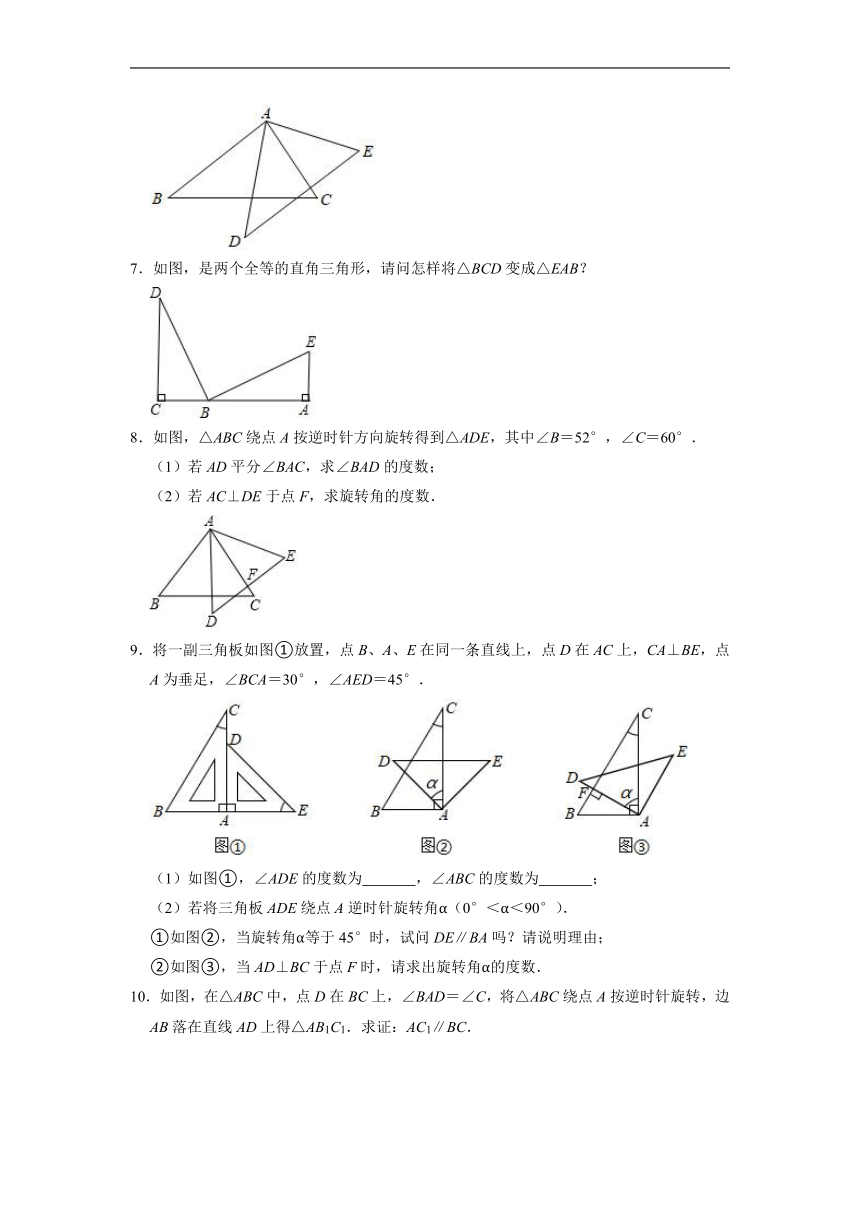
6.如图,△ABC绕着顶点A逆时针旋转到△ADE,∠B=40°,∠E=60°,AB∥DE,求∠DAC的度数.
7.如图,是两个全等的直角三角形,请问怎样将△BCD变成△EAB?
8.如图,△ABC绕点A按逆时针方向旋转得到△ADE,其中∠B=52°,∠C=60°.
(1)若AD平分∠BAC,求∠BAD的度数;
(2)若AC⊥DE于点F,求旋转角的度数.
9.将一副三角板如图①放置,点B、A、E在同一条直线上,点D在AC上,CA⊥BE,点A为垂足,∠BCA=30°,∠AED=45°.
(1)如图①,∠ADE的度数为 ,∠ABC的度数为 ;
(2)若将三角板ADE绕点A逆时针旋转角α(0°<α<90°).
①如图②,当旋转角α等于45°时,试问DE∥BA吗?请说明理由;
②如图③,当AD⊥BC于点F时,请求出旋转角α的度数.
10.如图,在△ABC中,点D在BC上,∠BAD=∠C,将△ABC绕点A按逆时针旋转,边AB落在直线AD上得△AB1C1.求证:AC1∥BC.
11.有两个形状、大小完全相同的直角三角板ABC和CDE,其中∠ACB=∠DCE=90°.将两个直角三角板ABC和CDE如图①放置,点A,C,E在直线MN上.
(1)三角板CDE位置不动,将三角板ABC绕点C顺时针旋转一周,
①在旋转过程中,若∠BCD=30°,则∠ACE= °;
②在旋转过程中,∠BCD与∠ACE有怎样的数量关系?请依据图②说明理由.
(2)在图①基础上,三角板ABC和CDE同时绕点C顺时针旋转,若三角板ABC的边AC从CM处开始绕点C顺时针旋转,转速为10°/秒,同时三角板CDE的边CE从CN处开始绕点C顺时针旋转,转速为1°/秒,当AC旋转一周再落到CM上时,两三角板都停止转动.如果设旋转时间为t秒,则在旋转过程中,当t= 秒时,有∠ACE=3∠BCD.
12.我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 示例图形 与对应线段有关的结论 与对应点有关的结论
平移 (1) AA′=BB′ AA′∥BB′
轴对称 (2) (3)
旋转 AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. (4)
13.如图,将Rt△AOB绕直角顶点O顺时针旋转得到Rt△COD,使点A的对应点C落在AB边上,过点D作DE∥AB,交AO的延长线于点E,求证:∠BCO=∠E.
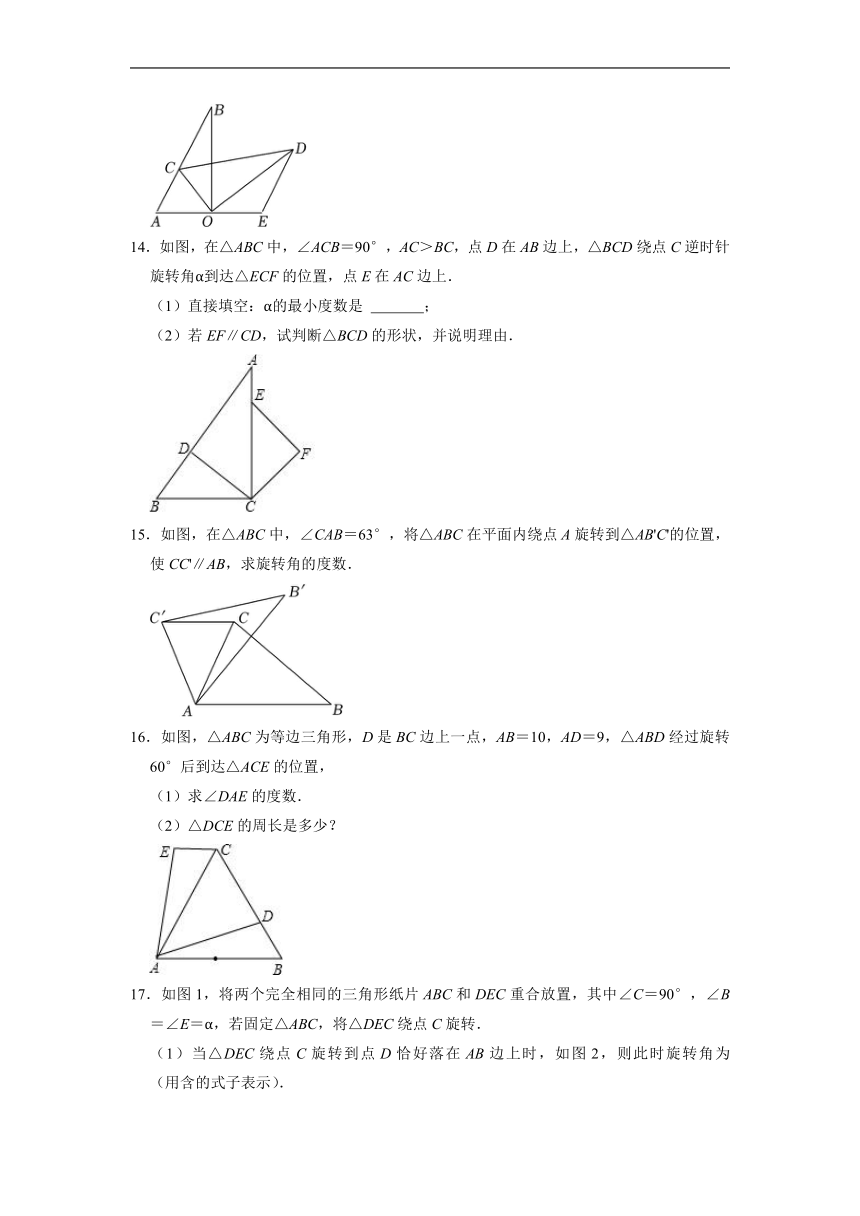
14.如图,在△ABC中,∠ACB=90°,AC>BC,点D在AB边上,△BCD绕点C逆时针旋转角α到达△ECF的位置,点E在AC边上.
(1)直接填空:α的最小度数是 ;
(2)若EF∥CD,试判断△BCD的形状,并说明理由.
15.如图,在△ABC中,∠CAB=63°,将△ABC在平面内绕点A旋转到△AB'C'的位置,使CC'∥AB,求旋转角的度数.
16.如图,△ABC为等边三角形,D是BC边上一点,AB=10,AD=9,△ABD经过旋转60°后到达△ACE的位置,
(1)求∠DAE的度数.
(2)△DCE的周长是多少?
17.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=α,若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC绕点C旋转到点D恰好落在AB边上时,如图2,则此时旋转角为 (用含的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
18.取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.
①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
19.在平面直角坐标系中,△ABC的顶点位置如图所示.
(1)作出△ABC关于x轴对称的图形△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 ;
(2)将△ABC绕原点逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
20.我们已经认识了图形的轴对称、平移和旋转.这是图形的三种基本变换,图形经过这样的变换,虽然位置发生了改变,但图形的形状与大小都不发生变化,反映了图形之间的全等关系.这种运用动态变换研究图形之间的关系的方法,是一种重要而且有效的方法,同学们学完了这些知识后,王老师在黑板上给大家出示了这样一道题目:
(1)如图,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连结BE,试说明AD=BE;聪明的小亮很快就找到了解决该问题的方法,请你帮小亮把说理过程补充完整.
解:∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°(等边三角形的性质)
∴∠ACD= (等式的性质).
∴△ACD绕点C按逆时针方向旋转 °,能够与 重合.
∴△ACD≌ (旋转变换的性质).
∴AD=BE( ).
(2)当同学们把这道题领会感悟后,王老师又在上题基础上追加了一问:试求∠AEB的度数.聪明的同学们你会解决吗?请写出你的求解过程(此问不用写推理依据).
参考答案
1.解:∵∠B=45°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=75°,
顺时针旋转30°时,如图1所示:
由旋转的性质得:∠B1AC1=∠BAC=75°,∠B1AB=30°,
∴∠BAC1=75°﹣30°=45°;
逆时针旋转30°时,如图2所示:
∠BAC1=75°+30°=105°;
综上所述,∠BAC1的度数为45°或105°.
2.(1)DB′=EC′,
证明:如图②,
∵AB=AC,D、E分别是AB、AC的中点,
∴AD=AE,
∵∠B′AC′=∠DAE=90°,
∴∠B′AD=∠C′AE=90°﹣∠DAC′,
在△B′AD和△C′AE中,
,
∴△B′AD≌△C′AE(SAS),
∴DB′=EC′.
(2)解:∵DB′∥AE,
∴∠ADB′=∠EAD=90°
又∵△B′AD≌△C′AE,
∴∠AEC′=∠ADB′,
∴∠AEC′=90°,
即△AEC′为直角三角形,
又∵AE=AC=AC′,
∴∠EC′A=30°,
∴α=90°﹣30°=60°;
(3)解:分为两种情况:
第一种情况:当P在DE上,①当AP=DP时,
∵∠ADP=45°,
∴∠DAP=∠ADP=45°,
∴α=90°﹣45°=45°;
②当AD=DP时,
∵∠ADP=45°,
∴∠DAP=∠DPA=(180°﹣∠ADP)=×(180°﹣45°)=67.5°,
∴α=90°﹣67.5°=22.5°;
第二种情况:当P点在ED延长线时,∵∠ADP=180°﹣45°=135°,
∴此时只能AD=AP,
∴∠APD=∠PAD=∠ADE=22.5°,
∴α=90°+22.5°=112.5°,
即旋转角α的度数是45°或22.5°或112.5°.
3.解:(1)如图(1),当DE∥AB时,∠EDF=∠BPF=45°
∵AF平分∠BAC,∠BAC=60°,
∴∠BAF=30°,
又∵∠BPF为△APF的一个外角,
∴∠PFA=∠BPF﹣∠BAF=45°﹣30°=15°,
∴t==3;
如图(2),当DE⊥AB时,
∠DPB=180°﹣90°﹣45°=45°,
∴∠APF=∠DPB=45°,
∵∠BAF=30°,
∴∠AFP=180°﹣∠APF﹣∠BAF=180°﹣45°﹣30°=105°,
∴t==21.
故答案为:3;21.
(2)①如图(3),当∠PAF=∠PFA时,
∵∠PAF=30°,
∴∠PFA=30°,
∴t=6;
②如图(4),当∠PFA=∠APF时,
∵∠PAF=30°,∠PAF+∠PFA+∠APF=180°,
∴∠AFP=(180°﹣30°)=75°,
∴t=15;
③如图(5),当∠PAF=∠APF时,
∠AFP=180°﹣∠PAF﹣∠APF=180°﹣30°﹣30°=120°,
∴t=24,
综上所述:当t为6或15或24时,△AFP有两个内角相等.
(3)x+y+z是为定值105,理由如下:
∵∠BMN是△AME的一个外角,∠MNB是△DFN的一个外角,
∴∠BMN=∠BAE+∠AED=x°+y°,∠MNB=∠DFB+∠D=z°+45°,
又∵∠BMN+∠MNB+∠B=180°,∠B=30°,
∴x°+y°+z°+45°+30°=180°,
∴x°+y°+z°=105°,
∴x+y+z=105.
4.解:(1)如图②,α=∠A′C′A=45°﹣30°=15°;
故答案为:15;
(2)如图③,过点A作AH⊥BC于点H,
∵∠C=30°,
∴AH=AC,
∵AD=AC,
∴DH==AC,
∴AH=DH,
∴∠HAD=45°,
∴∠HAC′=∠HAD+∠DAC′=90°,
∴HA⊥AC′,
∴BC∥A′C′;
(3)如图④,过点D作DH⊥AC,垂足为H,
∵AB=2,
∴AC=A′C′=2,
∴HC′=DH=A′C′=,
∴HC=×=3,
所以m的值为:HC﹣HC′=3﹣.
5.解:(1)当DE∥BC时,如图(1),
∵DE∥BC,
∴∠EDA=∠B=40°,
∵∠FDE=36°,
∴∠α=∠EDA﹣∠FDE=40°﹣36°=4°,
∴∠α=4°时,DE∥BC.
当DE⊥BC时,如图(2),
∵DE⊥BC,
∴∠BGD=90°,
∵∠B=40°,∠GDA是△GDB的一个外角,
∴∠GDA=∠B+∠BGD=40°+90°=130°,
∵∠EDF=36°,
∴∠α=∠GDA﹣∠FDE=130°﹣36°=94°,
∴∠α=94°时,DE⊥BC.
故答案为:4°;94°.
(2)
①∵∠ACB=90°,CD平分∠ACB,
∴∠BCD=45°,
∵∠ABC=40°,
∴∠ADC=∠ABC+∠BCD=40°+45°=85°,
当ED经过点C时,∠α=∠ADC﹣∠EDF=85°﹣36°=49°,
当FD经过点C时,∠α=∠ADC=85°,
∴顶点C在△DEF内部时,49°<α<85°.
∠1与∠2度数的和不发生变化,理由如下:
延长DC至点H,
∵∠NCH、∠MCH分别是△NCD和△MCD的外角,
∴∠NCH=∠2+∠NDC,∠MCH=∠1+∠MDC,
∴∠NCH+∠MCH=∠2+∠1+∠NDC+∠MDC,
∴∠NCM=∠1+∠2+∠NDM,
∵∠NCM=∠ACB=90°,∠NDM=∠FDE=36°,
∴90°=∠1+∠2+36°,
∴∠1+∠2=54°.
③∵∠ABC=40°,∠ACB﹣90°,
∴∠A=180°﹣40°﹣90°=50°,
∵∠ADF是△MBD的外角
∴∠α=∠ABC+∠1=40°+∠1,
∵∠2≥2∠1,∠1+∠2=54°,
∴54°﹣∠1≥2∠1,
∴∠1≤18°,
∴α≤58°,
又∵49°<α<85°,
∴49°<α≤58°.
6.解:∵△ABC绕着顶点A逆时针旋转到△ADE,
∴△ABC≌△ADE,
∴∠C=∠E=60°,∠D=∠B=40°,
∵∠B=40°,
∴∠BAC=180°﹣40°﹣60°=80°,
∵AB∥DE,
∴∠BAD=∠D=40°,
∴∠DAC=∠BAC﹣∠BAD=80°﹣40°=40°,
∴∠DAC的度数为40°.
7.解:先把△DCB以C为旋转中心逆时针旋转90°,然后再向右平移,使点C与A重合,这样△BCD变成△EAB.
8.解(1)在△ABC中,
∵∠B=52°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=68°,
∵AD分∠BAC,
∴∠BAD=;
(2)∵△ABC绕点A按逆时针方向旋转得到△ADE,
∴∠C=∠E=60°,
又∵AC⊥DE,
∴∠AFE=90°,
在△AFE中,
∵∠AFE=90°,∠E=60°,
∴∠EAF=30°,
即旋转角的度数为30°.
9.解:(1)∠ADE的度数为45°,∠ABC的度数为60°,
故答案为:45°,60°;
(2)①当旋转角α等于45°时,
∴∠BAC=90°,
又∠α=45°,
∴∠BAD=∠BAC﹣∠α=45°,
又∠ADE=45°
∴∠BAD=∠ADE,
∴DE∥BA;
②当AD⊥BC于点F时,
∴∠AFC=90°,
∵∠C=30°,
∴∠α=180°﹣∠AFC﹣∠C=180°﹣90°﹣30°=60°.
10.证明:根据旋转得出∠B=∠B1,∠C=∠C1,
∵∠B+∠BAD=∠B1+∠DFB1=∠ADC,
∴∠BAD=∠DFB1,
∵∠BAD=∠C,∠EFC=∠DFB1,
∴∠EFC=∠C1,
∴AC1∥BC.
11.解:(1)①在旋转过程中,若∠BCD=30°,则∠ACE=90°+90°﹣30°=150°或360°﹣90°﹣90°﹣30°=150°.
故答案为:150;
②∠BCD+∠ACE=180°,理由如下:
∵∠ACE=∠ACB+∠BCE,
∴∠BCD+∠ACE=∠BCD+∠ACB+∠BCE=∠ACB+∠DCE=90°+90°=180°;
(2)三角板ABC和CDE重合之前,
∠ACE=180°﹣9°t,∠BCD=9°t,
依题意有180°﹣9°t=3×9°t,
解得t=5;
三角板ABC和CDE重合之后,
∠ACE=9°t﹣180°,∠BCD=360°﹣9°t,
依题意有9°t﹣180°=3×(360°﹣9°t),
解得t=35.
故当t=5或35秒时,有∠ACE=3∠BCD.
故答案为:5或35.
12.解:(1)平移的性质:平移前后的对应线段相等且平行.所以与对应线段有关的结论为:AB=A′B′,AB∥A′B′;
(2)轴对称的性质:AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上.
(3)轴对称的性质:轴对称图形对称轴是任何一对对应点所连线段的垂直平分线.所以与对应点有关的结论为:l垂直平分AA′.
(4)OA=OA′,∠AOA′=∠BOB′.
故答案为:(1)AB=A′B′,AB∥A′B′;(2)AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上.;(3)l垂直平分AA′;(4)OA=OA′,∠AOA′=∠BOB′.
13.证明:∵将Rt△AOB绕直角顶点O顺时针旋转得到Rt△COD,
∴AO=CO,
∴∠A=∠ACO,
∵AB∥DE,
∴∠A+∠E=180°,
又∵∠ACO+∠BCO=180°,
∴∠BCO=∠E.
14.解:(1)∵△BCD绕点C逆时针旋转角α到达△ECF的位置,
而∠BCA=90°,
∴α的最小度数是270°;
(2)△BDC为直角三角形.理由如下:
∵△BCD绕点C逆时针旋转角α到达△ECF的位置,
∴∠DCF=∠BCA=90°,∠BDC=∠F,
∴EF∥CD,
∴∠DCF+∠F=180°,
∴∠F=90°,
∴∠BDC=90°,
∴△BDC为直角三角形.
15.解:∵CC′∥AB,
∴∠ACC′=∠CAB=63°,
∵△ABC在平面内绕点A旋转到△AB′C′的位置,
∴∠CAC′等于旋转角,AC=AC′,
∴∠ACC′=∠AC′C=63°,
∴∠CAC′=180°﹣∠ACC′﹣∠AC′C=180°﹣2×63°=54°,
∴旋转角为54°.
16.解:(1)△ABD经过旋转60°后到达△ACE的位置,
∴∠DAE=60°;
(2)如图,连接ED.
∵△ABC为等边三角形,AB=10,
∴BC=AB=10.
根据旋转的性质得到:AE=AD,CE=BD,
∵∠DAE=60°,
∴△DAE是等边三角形.
∴ED=AD.
又AD=9,
∴△DCE的周长=CD+CE+ED=BC+ED=10+9=19.即△DCE的周长是19.
17.解:(1)如图2,
∵∠C=90°,∠ABC=∠DEC=α,
∴∠BAC=90°﹣α,
∵△DEC绕点C旋转到点D恰好落在AB边上,
∴∠ACD等于旋转角,CD=CA,
∴∠CAD=∠CDA=90°﹣α,
∴∠ACD=180°﹣2(90°﹣α)=2α;
即旋转角为2α;
故答案为2α;
(2)小扬同学猜想是正确的,证明如下:
过B作BN⊥CD于N,过E作EM⊥AC于M,如图3,
∵∠ACB=∠DCE=90°,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
∵BN⊥CD于N,EM⊥AC于M,
∴∠BNC=∠EMC=90°,
∵△ACB≌△DCE,
∴BC=EC,
在△CBN和△CEM中
,
∴△CBN≌△CEM,
∴BN=EM,
∵S△BDC= CD BN,S△ACE= AC EM,
而CD=AC,
∴S△BCD=S△ACE.
18.解:(1)如图②,
∵AB∥DC,
∴∠BAC=∠C=30°,
∴α=∠BAC′﹣∠BAC=45°﹣30°=15°,
所以当α=15°时,AB∥DC;
(2)当旋转到图③所示位置时,α=45°,
(3)当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC值的大小不变.
证明:连接CC′,CD与BC′相交于O点,
在△BDO和△OCC′中,∠BOD=∠COC′,
∴∠BDO+∠DBO=∠OCC′+∠OC′C,
∴∠DBC′+∠CAC′+∠BDC=∠BDO+∠α+∠DBO=∠OCC′+∠OC′C+∠α
=180°﹣∠ACD﹣∠AC′B,
=180°﹣45°﹣30°=105°,
∴当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC值的大小不变.
19.解:(1)如图,△A1B1C1,即为所求,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是(a,﹣b);
故答案为:(a,﹣b);
(2)如图,△A2B2C2即为所求.
20.解:(1)∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°(等边三角形的性质)
∴∠ACD=∠BCE(等式的性质).
∴△ACD绕点C按逆时针方向旋转60°,能够与△BCE重合.
∴△ACD≌△BCE(旋转变换的性质).
∴AD=BE(全等三角形的对应边相等).
故答案为:∠BCE,60°,△BCE,△BCE,全等三角形的对应边相等;
(2)∵△DCE为等边三角形,
∴∠CDE=∠CED=60°,
∴∠ADC=180°﹣∠CDE=120°,
∵△ACD≌△BCE,
∴∠ADC=∠BEC=120°,
∴∠AEB=∠BEC﹣∠CED=60°.
1.如图,在△ABC中,∠B=45°,∠C=60°,将△ABC绕点A旋转30°后得到△AB1C1,求∠BAC1的度数.
2.如图①,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图②).
(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,求此时旋转角α的度数;
(3)如图③,在旋转过程中,设AC′与DE所在直线交于点P,当△ADP成为等腰三角形时,求此时的旋转角α的度数.(直接写出结果)
3.一副三角板如图1摆放,∠C=∠DFE=90°,∠B=30°,∠E=45°,点F在BC上,点A在DF上,且AF平分∠CAB,现将三角板DFE绕点F以每秒5°的速度顺时针旋转(当点D落在射线FB上时停止旋转),设旋转时间为t秒.
(1)当t= 秒时,DE∥AB;当t= 秒时,DE⊥AB;
(2)在旋转过程中,DF与AB的交点记为P,如图2,若△AFP有两个内角相等,求t的值;
(3)当边DE与边AB、BC分别交于点M、N时,如图3,连接AE,设∠BAE=x°,∠AED=y°,∠DFB=z°,试问x+y+z是否为定值?若是,请求出定值;若不是,请说明理由.
4.小志同学在玩一副直角三角尺时发现:含45°角的直角三角尺的斜边可与含30°角的直角三角尺的较长直角边完成重合(如图①),即△CD的顶点A′,C分别与△BAC的顶点A,C重合现在,他让△CDA固定不动,将△BAC通过变换使斜边BC经过△CDA的直角顶点D.
(1)如图②将△BAC绕点C按顺时针方向旋转a(0°<a<180°),使边BC经过点D,则a= ;
(2)如图③,将△BAC绕点A按逆时针方向旋转使边BC经过点D,求证:BC∥AC;
(3)如图④,若AB=2,将△BAC沿射线AC‘的方向平移m个单位长度使边BC经过点D,求m的值.
5.如图1,直角三角形DEF与直角三角形ABC的斜边在同一直线上,∠EDF=36°,∠ABC=40°,CD平分∠ACB,将△DEF绕点D按逆时针方向旋转,记∠ADF为α(0<α<180°),在旋转过程中:
(1)如图2,当∠α= 时,DE∥BC,当∠α= 时,DE⊥BC;
(2)如图3,当顶点C在△DEF内部时,边DF、DE分别交BC、AC的延长线于点M、N.
①此时∠α的度数范围是 ;
②∠1与∠2度数的和是否变化?若不变,求出∠1与∠2度数和;若变化,请说明理由.
③若使得∠2≥2∠1,求∠α的度数范围.
6.如图,△ABC绕着顶点A逆时针旋转到△ADE,∠B=40°,∠E=60°,AB∥DE,求∠DAC的度数.
7.如图,是两个全等的直角三角形,请问怎样将△BCD变成△EAB?
8.如图,△ABC绕点A按逆时针方向旋转得到△ADE,其中∠B=52°,∠C=60°.
(1)若AD平分∠BAC,求∠BAD的度数;
(2)若AC⊥DE于点F,求旋转角的度数.
9.将一副三角板如图①放置,点B、A、E在同一条直线上,点D在AC上,CA⊥BE,点A为垂足,∠BCA=30°,∠AED=45°.
(1)如图①,∠ADE的度数为 ,∠ABC的度数为 ;
(2)若将三角板ADE绕点A逆时针旋转角α(0°<α<90°).
①如图②,当旋转角α等于45°时,试问DE∥BA吗?请说明理由;
②如图③,当AD⊥BC于点F时,请求出旋转角α的度数.
10.如图,在△ABC中,点D在BC上,∠BAD=∠C,将△ABC绕点A按逆时针旋转,边AB落在直线AD上得△AB1C1.求证:AC1∥BC.
11.有两个形状、大小完全相同的直角三角板ABC和CDE,其中∠ACB=∠DCE=90°.将两个直角三角板ABC和CDE如图①放置,点A,C,E在直线MN上.
(1)三角板CDE位置不动,将三角板ABC绕点C顺时针旋转一周,
①在旋转过程中,若∠BCD=30°,则∠ACE= °;
②在旋转过程中,∠BCD与∠ACE有怎样的数量关系?请依据图②说明理由.
(2)在图①基础上,三角板ABC和CDE同时绕点C顺时针旋转,若三角板ABC的边AC从CM处开始绕点C顺时针旋转,转速为10°/秒,同时三角板CDE的边CE从CN处开始绕点C顺时针旋转,转速为1°/秒,当AC旋转一周再落到CM上时,两三角板都停止转动.如果设旋转时间为t秒,则在旋转过程中,当t= 秒时,有∠ACE=3∠BCD.
12.我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 示例图形 与对应线段有关的结论 与对应点有关的结论
平移 (1) AA′=BB′ AA′∥BB′
轴对称 (2) (3)
旋转 AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. (4)
13.如图,将Rt△AOB绕直角顶点O顺时针旋转得到Rt△COD,使点A的对应点C落在AB边上,过点D作DE∥AB,交AO的延长线于点E,求证:∠BCO=∠E.
14.如图,在△ABC中,∠ACB=90°,AC>BC,点D在AB边上,△BCD绕点C逆时针旋转角α到达△ECF的位置,点E在AC边上.
(1)直接填空:α的最小度数是 ;
(2)若EF∥CD,试判断△BCD的形状,并说明理由.
15.如图,在△ABC中,∠CAB=63°,将△ABC在平面内绕点A旋转到△AB'C'的位置,使CC'∥AB,求旋转角的度数.
16.如图,△ABC为等边三角形,D是BC边上一点,AB=10,AD=9,△ABD经过旋转60°后到达△ACE的位置,
(1)求∠DAE的度数.
(2)△DCE的周长是多少?
17.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=α,若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC绕点C旋转到点D恰好落在AB边上时,如图2,则此时旋转角为 (用含的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
18.取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.
①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
19.在平面直角坐标系中,△ABC的顶点位置如图所示.
(1)作出△ABC关于x轴对称的图形△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 ;
(2)将△ABC绕原点逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
20.我们已经认识了图形的轴对称、平移和旋转.这是图形的三种基本变换,图形经过这样的变换,虽然位置发生了改变,但图形的形状与大小都不发生变化,反映了图形之间的全等关系.这种运用动态变换研究图形之间的关系的方法,是一种重要而且有效的方法,同学们学完了这些知识后,王老师在黑板上给大家出示了这样一道题目:
(1)如图,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连结BE,试说明AD=BE;聪明的小亮很快就找到了解决该问题的方法,请你帮小亮把说理过程补充完整.
解:∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°(等边三角形的性质)
∴∠ACD= (等式的性质).
∴△ACD绕点C按逆时针方向旋转 °,能够与 重合.
∴△ACD≌ (旋转变换的性质).
∴AD=BE( ).
(2)当同学们把这道题领会感悟后,王老师又在上题基础上追加了一问:试求∠AEB的度数.聪明的同学们你会解决吗?请写出你的求解过程(此问不用写推理依据).
参考答案
1.解:∵∠B=45°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=75°,
顺时针旋转30°时,如图1所示:
由旋转的性质得:∠B1AC1=∠BAC=75°,∠B1AB=30°,
∴∠BAC1=75°﹣30°=45°;
逆时针旋转30°时,如图2所示:
∠BAC1=75°+30°=105°;
综上所述,∠BAC1的度数为45°或105°.
2.(1)DB′=EC′,
证明:如图②,
∵AB=AC,D、E分别是AB、AC的中点,
∴AD=AE,
∵∠B′AC′=∠DAE=90°,
∴∠B′AD=∠C′AE=90°﹣∠DAC′,
在△B′AD和△C′AE中,
,
∴△B′AD≌△C′AE(SAS),
∴DB′=EC′.
(2)解:∵DB′∥AE,
∴∠ADB′=∠EAD=90°
又∵△B′AD≌△C′AE,
∴∠AEC′=∠ADB′,
∴∠AEC′=90°,
即△AEC′为直角三角形,
又∵AE=AC=AC′,
∴∠EC′A=30°,
∴α=90°﹣30°=60°;
(3)解:分为两种情况:
第一种情况:当P在DE上,①当AP=DP时,
∵∠ADP=45°,
∴∠DAP=∠ADP=45°,
∴α=90°﹣45°=45°;
②当AD=DP时,
∵∠ADP=45°,
∴∠DAP=∠DPA=(180°﹣∠ADP)=×(180°﹣45°)=67.5°,
∴α=90°﹣67.5°=22.5°;
第二种情况:当P点在ED延长线时,∵∠ADP=180°﹣45°=135°,
∴此时只能AD=AP,
∴∠APD=∠PAD=∠ADE=22.5°,
∴α=90°+22.5°=112.5°,
即旋转角α的度数是45°或22.5°或112.5°.
3.解:(1)如图(1),当DE∥AB时,∠EDF=∠BPF=45°
∵AF平分∠BAC,∠BAC=60°,
∴∠BAF=30°,
又∵∠BPF为△APF的一个外角,
∴∠PFA=∠BPF﹣∠BAF=45°﹣30°=15°,
∴t==3;
如图(2),当DE⊥AB时,
∠DPB=180°﹣90°﹣45°=45°,
∴∠APF=∠DPB=45°,
∵∠BAF=30°,
∴∠AFP=180°﹣∠APF﹣∠BAF=180°﹣45°﹣30°=105°,
∴t==21.
故答案为:3;21.
(2)①如图(3),当∠PAF=∠PFA时,
∵∠PAF=30°,
∴∠PFA=30°,
∴t=6;
②如图(4),当∠PFA=∠APF时,
∵∠PAF=30°,∠PAF+∠PFA+∠APF=180°,
∴∠AFP=(180°﹣30°)=75°,
∴t=15;
③如图(5),当∠PAF=∠APF时,
∠AFP=180°﹣∠PAF﹣∠APF=180°﹣30°﹣30°=120°,
∴t=24,
综上所述:当t为6或15或24时,△AFP有两个内角相等.
(3)x+y+z是为定值105,理由如下:
∵∠BMN是△AME的一个外角,∠MNB是△DFN的一个外角,
∴∠BMN=∠BAE+∠AED=x°+y°,∠MNB=∠DFB+∠D=z°+45°,
又∵∠BMN+∠MNB+∠B=180°,∠B=30°,
∴x°+y°+z°+45°+30°=180°,
∴x°+y°+z°=105°,
∴x+y+z=105.
4.解:(1)如图②,α=∠A′C′A=45°﹣30°=15°;
故答案为:15;
(2)如图③,过点A作AH⊥BC于点H,
∵∠C=30°,
∴AH=AC,
∵AD=AC,
∴DH==AC,
∴AH=DH,
∴∠HAD=45°,
∴∠HAC′=∠HAD+∠DAC′=90°,
∴HA⊥AC′,
∴BC∥A′C′;
(3)如图④,过点D作DH⊥AC,垂足为H,
∵AB=2,
∴AC=A′C′=2,
∴HC′=DH=A′C′=,
∴HC=×=3,
所以m的值为:HC﹣HC′=3﹣.
5.解:(1)当DE∥BC时,如图(1),
∵DE∥BC,
∴∠EDA=∠B=40°,
∵∠FDE=36°,
∴∠α=∠EDA﹣∠FDE=40°﹣36°=4°,
∴∠α=4°时,DE∥BC.
当DE⊥BC时,如图(2),
∵DE⊥BC,
∴∠BGD=90°,
∵∠B=40°,∠GDA是△GDB的一个外角,
∴∠GDA=∠B+∠BGD=40°+90°=130°,
∵∠EDF=36°,
∴∠α=∠GDA﹣∠FDE=130°﹣36°=94°,
∴∠α=94°时,DE⊥BC.
故答案为:4°;94°.
(2)
①∵∠ACB=90°,CD平分∠ACB,
∴∠BCD=45°,
∵∠ABC=40°,
∴∠ADC=∠ABC+∠BCD=40°+45°=85°,
当ED经过点C时,∠α=∠ADC﹣∠EDF=85°﹣36°=49°,
当FD经过点C时,∠α=∠ADC=85°,
∴顶点C在△DEF内部时,49°<α<85°.
∠1与∠2度数的和不发生变化,理由如下:
延长DC至点H,
∵∠NCH、∠MCH分别是△NCD和△MCD的外角,
∴∠NCH=∠2+∠NDC,∠MCH=∠1+∠MDC,
∴∠NCH+∠MCH=∠2+∠1+∠NDC+∠MDC,
∴∠NCM=∠1+∠2+∠NDM,
∵∠NCM=∠ACB=90°,∠NDM=∠FDE=36°,
∴90°=∠1+∠2+36°,
∴∠1+∠2=54°.
③∵∠ABC=40°,∠ACB﹣90°,
∴∠A=180°﹣40°﹣90°=50°,
∵∠ADF是△MBD的外角
∴∠α=∠ABC+∠1=40°+∠1,
∵∠2≥2∠1,∠1+∠2=54°,
∴54°﹣∠1≥2∠1,
∴∠1≤18°,
∴α≤58°,
又∵49°<α<85°,
∴49°<α≤58°.
6.解:∵△ABC绕着顶点A逆时针旋转到△ADE,
∴△ABC≌△ADE,
∴∠C=∠E=60°,∠D=∠B=40°,
∵∠B=40°,
∴∠BAC=180°﹣40°﹣60°=80°,
∵AB∥DE,
∴∠BAD=∠D=40°,
∴∠DAC=∠BAC﹣∠BAD=80°﹣40°=40°,
∴∠DAC的度数为40°.
7.解:先把△DCB以C为旋转中心逆时针旋转90°,然后再向右平移,使点C与A重合,这样△BCD变成△EAB.
8.解(1)在△ABC中,
∵∠B=52°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=68°,
∵AD分∠BAC,
∴∠BAD=;
(2)∵△ABC绕点A按逆时针方向旋转得到△ADE,
∴∠C=∠E=60°,
又∵AC⊥DE,
∴∠AFE=90°,
在△AFE中,
∵∠AFE=90°,∠E=60°,
∴∠EAF=30°,
即旋转角的度数为30°.
9.解:(1)∠ADE的度数为45°,∠ABC的度数为60°,
故答案为:45°,60°;
(2)①当旋转角α等于45°时,
∴∠BAC=90°,
又∠α=45°,
∴∠BAD=∠BAC﹣∠α=45°,
又∠ADE=45°
∴∠BAD=∠ADE,
∴DE∥BA;
②当AD⊥BC于点F时,
∴∠AFC=90°,
∵∠C=30°,
∴∠α=180°﹣∠AFC﹣∠C=180°﹣90°﹣30°=60°.
10.证明:根据旋转得出∠B=∠B1,∠C=∠C1,
∵∠B+∠BAD=∠B1+∠DFB1=∠ADC,
∴∠BAD=∠DFB1,
∵∠BAD=∠C,∠EFC=∠DFB1,
∴∠EFC=∠C1,
∴AC1∥BC.
11.解:(1)①在旋转过程中,若∠BCD=30°,则∠ACE=90°+90°﹣30°=150°或360°﹣90°﹣90°﹣30°=150°.
故答案为:150;
②∠BCD+∠ACE=180°,理由如下:
∵∠ACE=∠ACB+∠BCE,
∴∠BCD+∠ACE=∠BCD+∠ACB+∠BCE=∠ACB+∠DCE=90°+90°=180°;
(2)三角板ABC和CDE重合之前,
∠ACE=180°﹣9°t,∠BCD=9°t,
依题意有180°﹣9°t=3×9°t,
解得t=5;
三角板ABC和CDE重合之后,
∠ACE=9°t﹣180°,∠BCD=360°﹣9°t,
依题意有9°t﹣180°=3×(360°﹣9°t),
解得t=35.
故当t=5或35秒时,有∠ACE=3∠BCD.
故答案为:5或35.
12.解:(1)平移的性质:平移前后的对应线段相等且平行.所以与对应线段有关的结论为:AB=A′B′,AB∥A′B′;
(2)轴对称的性质:AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上.
(3)轴对称的性质:轴对称图形对称轴是任何一对对应点所连线段的垂直平分线.所以与对应点有关的结论为:l垂直平分AA′.
(4)OA=OA′,∠AOA′=∠BOB′.
故答案为:(1)AB=A′B′,AB∥A′B′;(2)AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上.;(3)l垂直平分AA′;(4)OA=OA′,∠AOA′=∠BOB′.
13.证明:∵将Rt△AOB绕直角顶点O顺时针旋转得到Rt△COD,
∴AO=CO,
∴∠A=∠ACO,
∵AB∥DE,
∴∠A+∠E=180°,
又∵∠ACO+∠BCO=180°,
∴∠BCO=∠E.
14.解:(1)∵△BCD绕点C逆时针旋转角α到达△ECF的位置,
而∠BCA=90°,
∴α的最小度数是270°;
(2)△BDC为直角三角形.理由如下:
∵△BCD绕点C逆时针旋转角α到达△ECF的位置,
∴∠DCF=∠BCA=90°,∠BDC=∠F,
∴EF∥CD,
∴∠DCF+∠F=180°,
∴∠F=90°,
∴∠BDC=90°,
∴△BDC为直角三角形.
15.解:∵CC′∥AB,
∴∠ACC′=∠CAB=63°,
∵△ABC在平面内绕点A旋转到△AB′C′的位置,
∴∠CAC′等于旋转角,AC=AC′,
∴∠ACC′=∠AC′C=63°,
∴∠CAC′=180°﹣∠ACC′﹣∠AC′C=180°﹣2×63°=54°,
∴旋转角为54°.
16.解:(1)△ABD经过旋转60°后到达△ACE的位置,
∴∠DAE=60°;
(2)如图,连接ED.
∵△ABC为等边三角形,AB=10,
∴BC=AB=10.
根据旋转的性质得到:AE=AD,CE=BD,
∵∠DAE=60°,
∴△DAE是等边三角形.
∴ED=AD.
又AD=9,
∴△DCE的周长=CD+CE+ED=BC+ED=10+9=19.即△DCE的周长是19.
17.解:(1)如图2,
∵∠C=90°,∠ABC=∠DEC=α,
∴∠BAC=90°﹣α,
∵△DEC绕点C旋转到点D恰好落在AB边上,
∴∠ACD等于旋转角,CD=CA,
∴∠CAD=∠CDA=90°﹣α,
∴∠ACD=180°﹣2(90°﹣α)=2α;
即旋转角为2α;
故答案为2α;
(2)小扬同学猜想是正确的,证明如下:
过B作BN⊥CD于N,过E作EM⊥AC于M,如图3,
∵∠ACB=∠DCE=90°,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
∵BN⊥CD于N,EM⊥AC于M,
∴∠BNC=∠EMC=90°,
∵△ACB≌△DCE,
∴BC=EC,
在△CBN和△CEM中
,
∴△CBN≌△CEM,
∴BN=EM,
∵S△BDC= CD BN,S△ACE= AC EM,
而CD=AC,
∴S△BCD=S△ACE.
18.解:(1)如图②,
∵AB∥DC,
∴∠BAC=∠C=30°,
∴α=∠BAC′﹣∠BAC=45°﹣30°=15°,
所以当α=15°时,AB∥DC;
(2)当旋转到图③所示位置时,α=45°,
(3)当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC值的大小不变.
证明:连接CC′,CD与BC′相交于O点,
在△BDO和△OCC′中,∠BOD=∠COC′,
∴∠BDO+∠DBO=∠OCC′+∠OC′C,
∴∠DBC′+∠CAC′+∠BDC=∠BDO+∠α+∠DBO=∠OCC′+∠OC′C+∠α
=180°﹣∠ACD﹣∠AC′B,
=180°﹣45°﹣30°=105°,
∴当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC值的大小不变.
19.解:(1)如图,△A1B1C1,即为所求,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是(a,﹣b);
故答案为:(a,﹣b);
(2)如图,△A2B2C2即为所求.
20.解:(1)∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°(等边三角形的性质)
∴∠ACD=∠BCE(等式的性质).
∴△ACD绕点C按逆时针方向旋转60°,能够与△BCE重合.
∴△ACD≌△BCE(旋转变换的性质).
∴AD=BE(全等三角形的对应边相等).
故答案为:∠BCE,60°,△BCE,△BCE,全等三角形的对应边相等;
(2)∵△DCE为等边三角形,
∴∠CDE=∠CED=60°,
∴∠ADC=180°﹣∠CDE=120°,
∵△ACD≌△BCE,
∴∠ADC=∠BEC=120°,
∴∠AEB=∠BEC﹣∠CED=60°.
同课章节目录
