24.2.2 直线和圆的位置关系
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 |  | |
| 格式 | zip | ||
| 文件大小 | 683.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-30 14:20:19 | ||
图片预览




文档简介
课件20张PPT。直线和圆的位置有何关系?直线和圆的位置关系第24章学习目标 探索直线和圆的位置关系中圆心到直线的距离与圆的半径之间的数量关系.知道直线和圆的位置关系.重点:掌握直线和圆的三种位置关系的性质与判定。
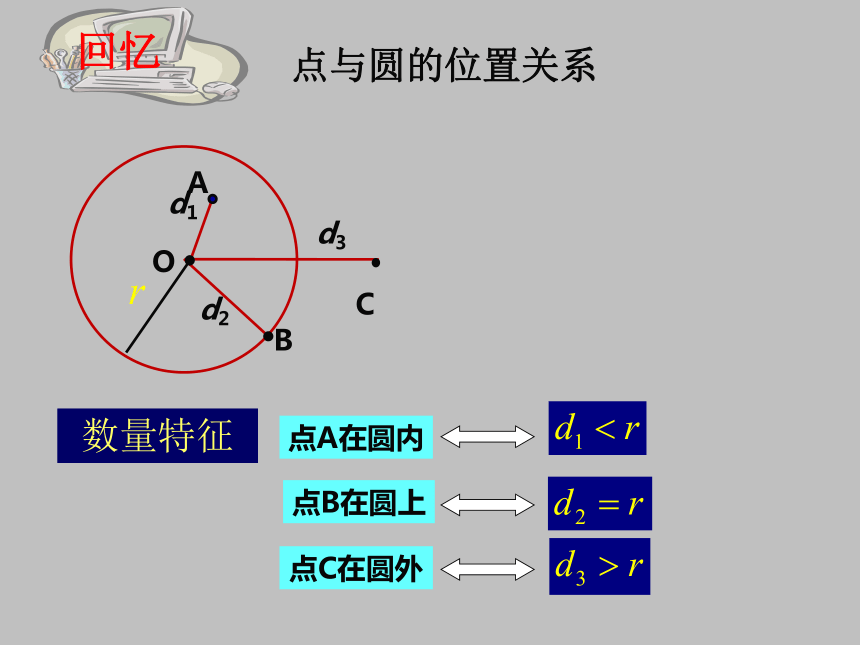
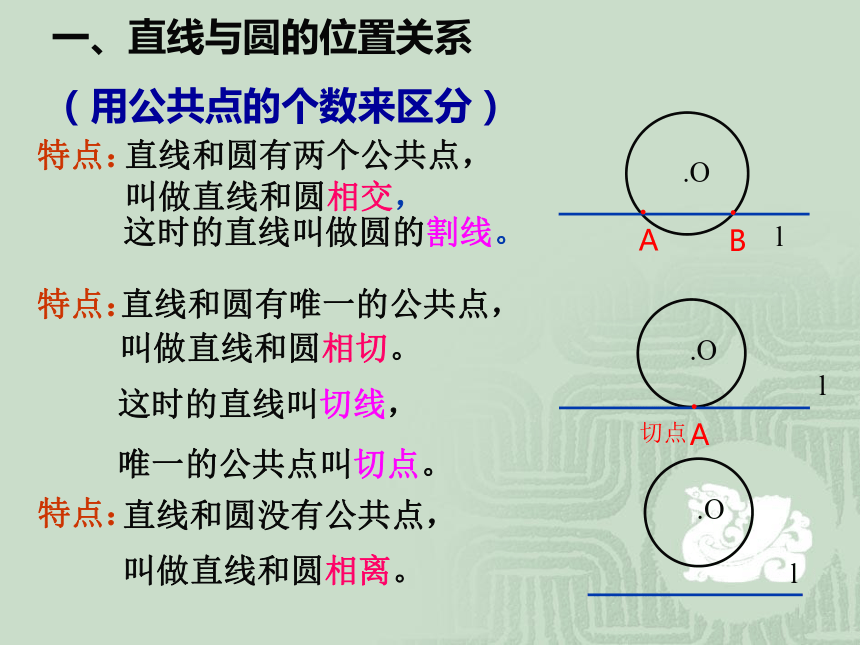
难点:发现隐含在图形中的两个数量d和r并加以比较。点与圆的位置关系点B在圆上点A在圆内点C在圆外数量特征回忆.Ol特点:.O叫做直线和圆相离。直线和圆没有公共点,l特点:直线和圆有唯一的公共点,叫做直线和圆相切。这时的直线叫切线,
唯一的公共点叫切点。.Ol特点:直线和圆有两个公共点,叫做直线和圆相交,这时的直线叫做圆的割线。一、直线与圆的位置关系
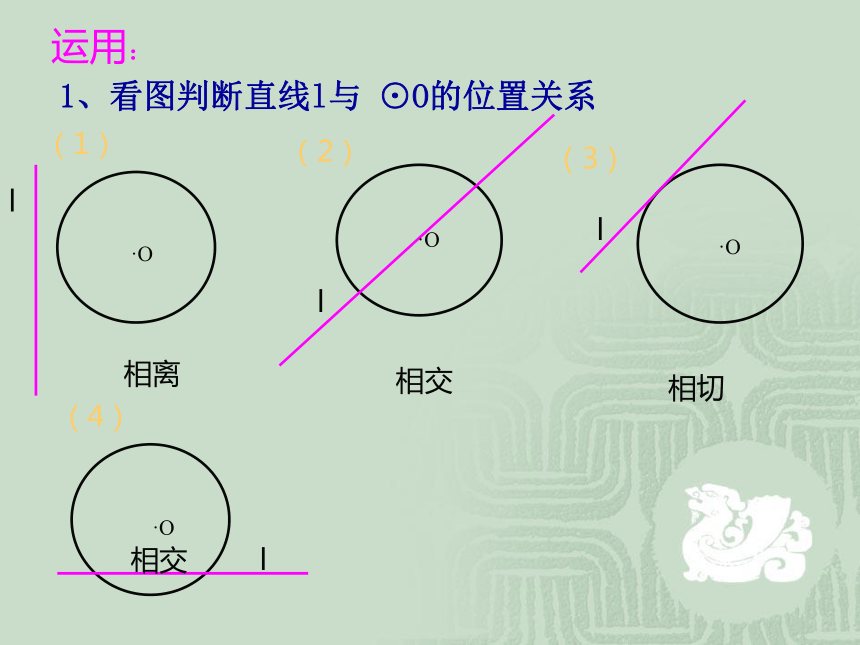
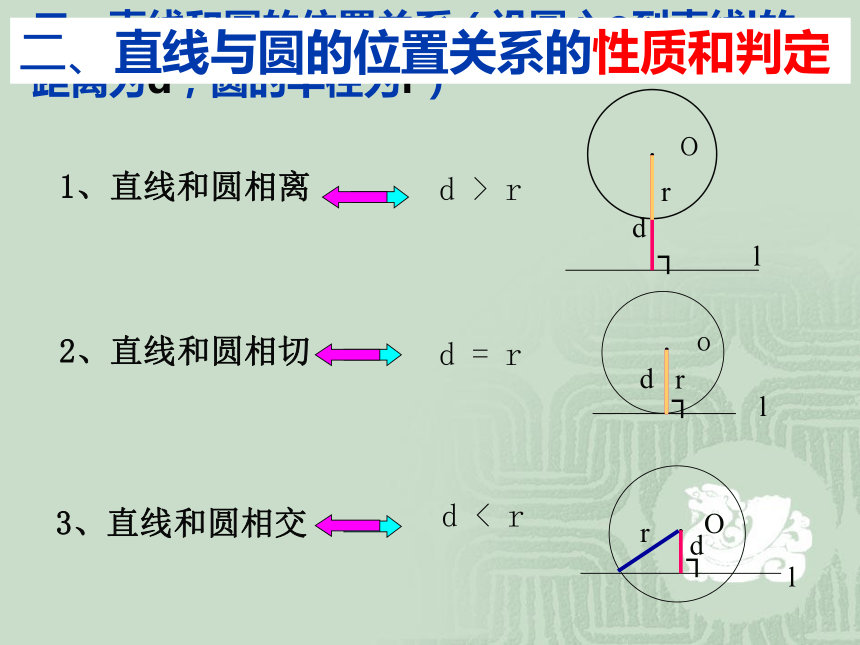
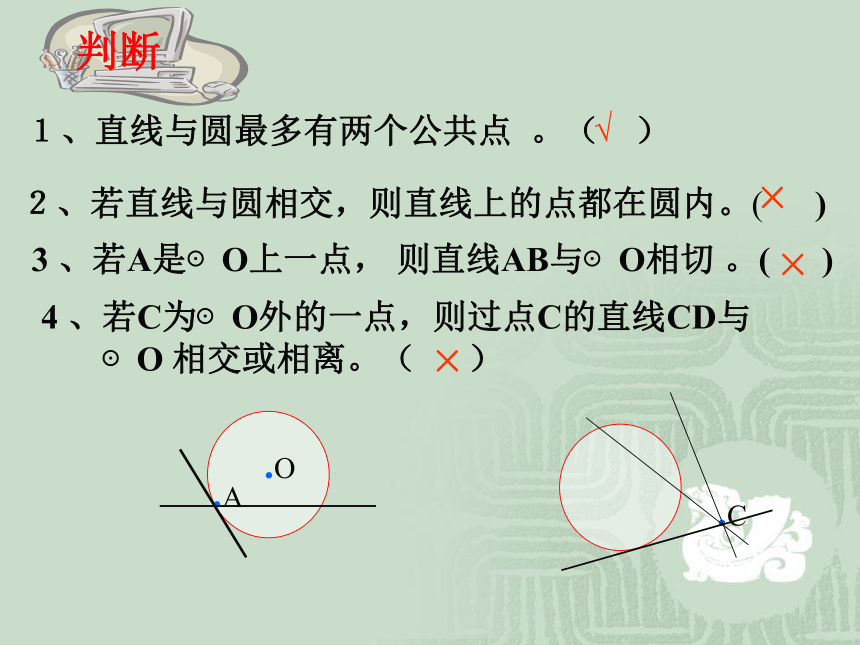
(用公共点的个数来区分).A.A.B切点运用:1、看图判断直线l与 ⊙O的位置关系(1)(2)(3)(4)相离相切相交相交llll·O·O·O·O2、直线和圆相切d = r3、直线和圆相交d < rd二、直线和圆的位置关系(设圆心o到直线l的距离为d,圆的半径为r)1、直线和圆相离d > r二、直线与圆的位置关系的性质和判定r 1、直线与圆最多有两个公共点 。( ) √×判断3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( ).A.O2、若直线与圆相交,则直线上的点都在圆内。( ) 4 、若C为⊙O外的一点,则过点C的直线CD与
⊙O 相交或相离。( )××.C相交相切相离d > 5cmd = 5cmd < 5cm练习20cm≤210例题1:O 已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是___ 。BC43相离相切例题2:分析在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与直线AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。BCAD453?例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。ABCAD453d=2.4思考:当 r 满足 _______时,
⊙C与线段AB只有一个公共点. 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆。想一想? 当r满足________________________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm 1、如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样的位置关系?为什么 ? ⑴ r =2cm; ⑵ r =4cm; ⑶ r =2.5cm。 解:过点M作MC⊥OA于C ,
∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm ⑴ ∵ d=MC=2.5, r=2 即d >r
∴ ⊙M与OA相离;
⑵ ∵ d=MC=2.5, r=4 即d < r
∴ ⊙M与OA相交;
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙M与OA相切.课堂练习.2.识别直线与圆的位置关系的方法:
1.直线与圆的位置关系三种:相离、相切和相交.小 结 (2)另一种是根据圆心到直线的距离d与圆半径r的大小
关系来进行识别:
直线l与⊙O没有公共点 直线l与⊙O相离.
直线l与⊙O只有一个公共点 直线l与⊙O相切.
直线l与⊙O有两个公共点 直线l与⊙O相交. d >r 直线l与⊙O相离;
d =r 直线l与⊙O相切;
d(1)一种是根据定义进行识别: 随堂检测
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.直线l上的一点到圆心O的距离等于⊙O的半径,则直线l与⊙O( )
A、相离 B、相切 C、相交 D、相切或相交。
3.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.
AD相离4.若d,r是方程 的两个根,且直线m与⊙O的
位置关系是相切,则a的值是 。4你学会了吗一.直线和圆的三种位置关系二.判断直线和圆的位置关系的方法1.利用定义2.利用d和r作业:
必做:课本94页练习
选做:如图:菱形ABCD的边长为5cm,∠B=60°当以A为圆心的圆与BC相切时,半径是 ,此时⊙A与CD的位置关系是 。?谢谢,再见!
难点:发现隐含在图形中的两个数量d和r并加以比较。点与圆的位置关系点B在圆上点A在圆内点C在圆外数量特征回忆.Ol特点:.O叫做直线和圆相离。直线和圆没有公共点,l特点:直线和圆有唯一的公共点,叫做直线和圆相切。这时的直线叫切线,
唯一的公共点叫切点。.Ol特点:直线和圆有两个公共点,叫做直线和圆相交,这时的直线叫做圆的割线。一、直线与圆的位置关系
(用公共点的个数来区分).A.A.B切点运用:1、看图判断直线l与 ⊙O的位置关系(1)(2)(3)(4)相离相切相交相交llll·O·O·O·O2、直线和圆相切d = r3、直线和圆相交d < rd二、直线和圆的位置关系(设圆心o到直线l的距离为d,圆的半径为r)1、直线和圆相离d > r二、直线与圆的位置关系的性质和判定r 1、直线与圆最多有两个公共点 。( ) √×判断3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( ).A.O2、若直线与圆相交,则直线上的点都在圆内。( ) 4 、若C为⊙O外的一点,则过点C的直线CD与
⊙O 相交或相离。( )××.C相交相切相离d > 5cmd = 5cmd < 5cm练习20cm≤210例题1:O 已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是___ 。BC43相离相切例题2:分析在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与直线AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。BCAD453?例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。ABCAD453d=2.4思考:当 r 满足 _______时,
⊙C与线段AB只有一个公共点. 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆。想一想? 当r满足________________________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm
∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm ⑴ ∵ d=MC=2.5, r=2 即d >r
∴ ⊙M与OA相离;
⑵ ∵ d=MC=2.5, r=4 即d < r
∴ ⊙M与OA相交;
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙M与OA相切.课堂练习.2.识别直线与圆的位置关系的方法:
1.直线与圆的位置关系三种:相离、相切和相交.小 结 (2)另一种是根据圆心到直线的距离d与圆半径r的大小
关系来进行识别:
直线l与⊙O没有公共点 直线l与⊙O相离.
直线l与⊙O只有一个公共点 直线l与⊙O相切.
直线l与⊙O有两个公共点 直线l与⊙O相交. d >r 直线l与⊙O相离;
d =r 直线l与⊙O相切;
d
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.直线l上的一点到圆心O的距离等于⊙O的半径,则直线l与⊙O( )
A、相离 B、相切 C、相交 D、相切或相交。
3.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.
AD相离4.若d,r是方程 的两个根,且直线m与⊙O的
位置关系是相切,则a的值是 。4你学会了吗一.直线和圆的三种位置关系二.判断直线和圆的位置关系的方法1.利用定义2.利用d和r作业:
必做:课本94页练习
选做:如图:菱形ABCD的边长为5cm,∠B=60°当以A为圆心的圆与BC相切时,半径是 ,此时⊙A与CD的位置关系是 。?谢谢,再见!
同课章节目录
