数学人教A版(2019)选择性必修第一册第一章 空间向量与立体几何 章节检测 (有答案)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册第一章 空间向量与立体几何 章节检测 (有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 323.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 10:37:06 | ||
图片预览


文档简介
高中数学人教A版(2019)选择性必修一立体几何与空间向量章节检测
一、单选题
1.已知平面 的一个法向量 ,点 在平面 内,则点 到平面 的距离为( )
A. B. C. D.
2.如图,在正三棱柱 中, ,则异面直线 与 所成角的余弦值是( )
A.0 B. C. D.
3.如图,直三棱柱 中, ,点P在棱 上,且三棱锥A-PBC的体积为4,则直线 与平面PBC所成角的正弦值等于( )
A. B. C. D.
4.三棱锥 中, 底面ABC, , ,D为AB的中点, ,则点D到面 的距离等于( )
A. B. C. D.
5.在正方体 中, , , 分别是棱 , , 的中点,下列说法错误的是( )
A. B. 与 是异面直线
C. , , , 四点共面 D.直线 与平面 相交
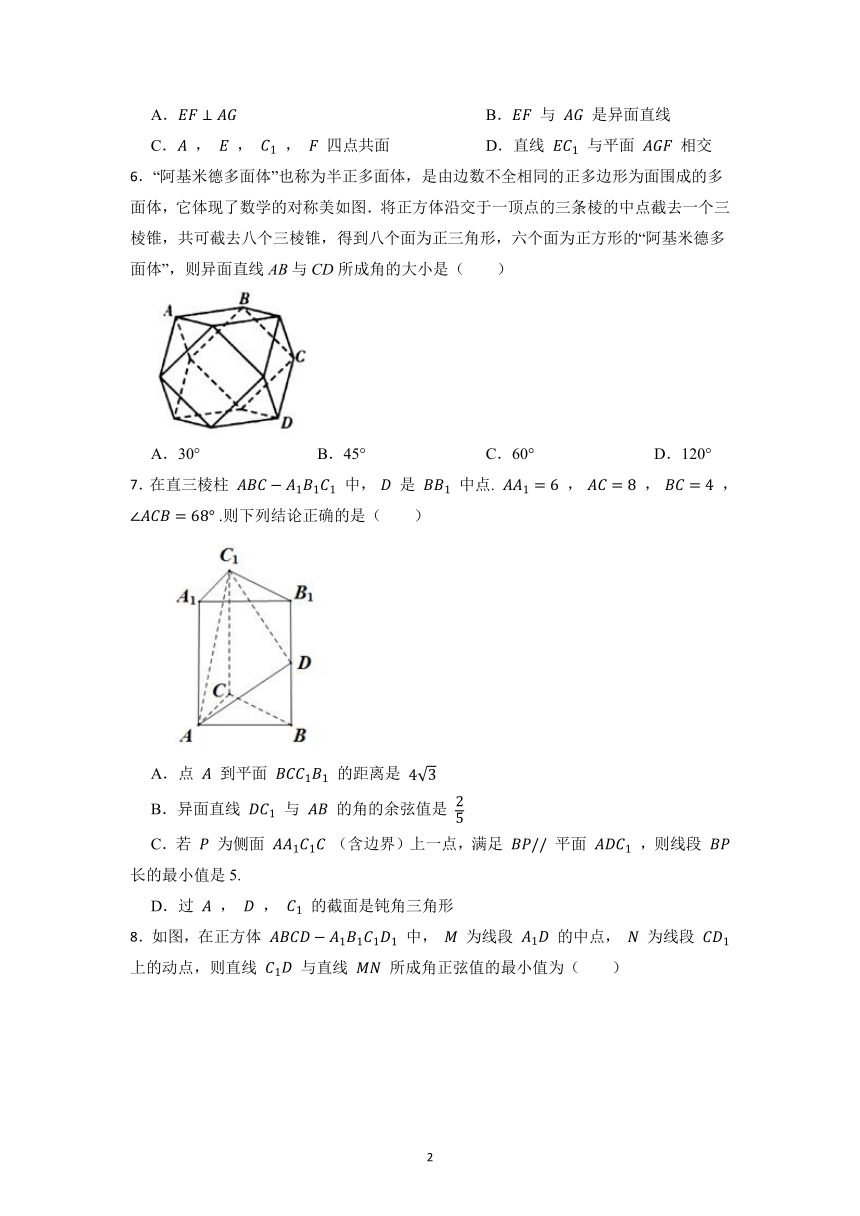
6.“阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美如图.将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形,六个面为正方形的“阿基米德多面体”,则异面直线AB与CD所成角的大小是( )
A.30° B.45° C.60° D.120°
7.在直三棱柱 中, 是 中点. , , , .则下列结论正确的是( )
A.点 到平面 的距离是
B.异面直线 与 的角的余弦值是
C.若 为侧面 (含边界)上一点,满足 平面 ,则线段 长的最小值是5.
D.过 , , 的截面是钝角三角形
8.如图,在正方体 中, 为线段 的中点, 为线段 上的动点,则直线 与直线 所成角正弦值的最小值为( )
A. B. C. D.
二、多选题
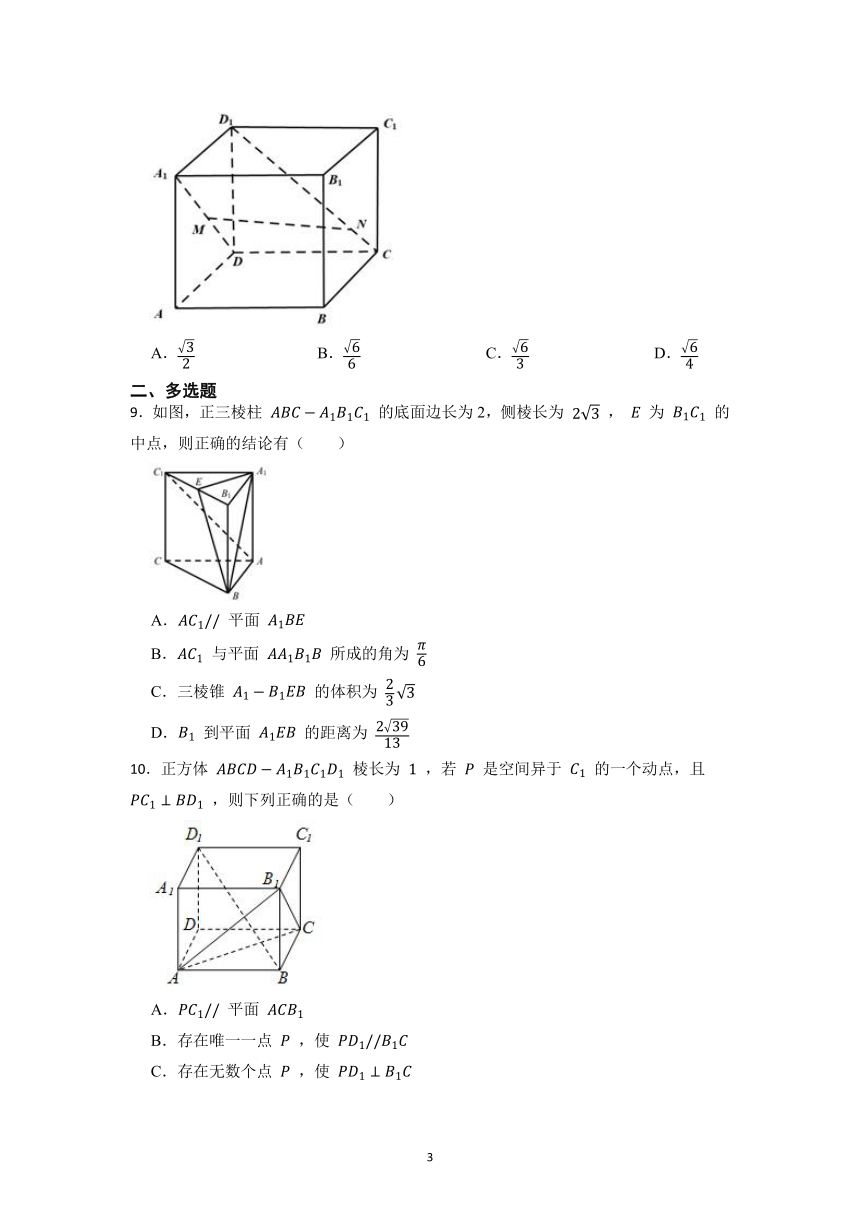
9.如图,正三棱柱 的底面边长为2,侧棱长为 , 为 的中点,则正确的结论有( )
A. 平面
B. 与平面 所成的角为
C.三棱锥 的体积为
D. 到平面 的距离为
10.正方体 棱长为 ,若 是空间异于 的一个动点,且 ,则下列正确的是( )
A. 平面
B.存在唯一一点 ,使
C.存在无数个点 ,使
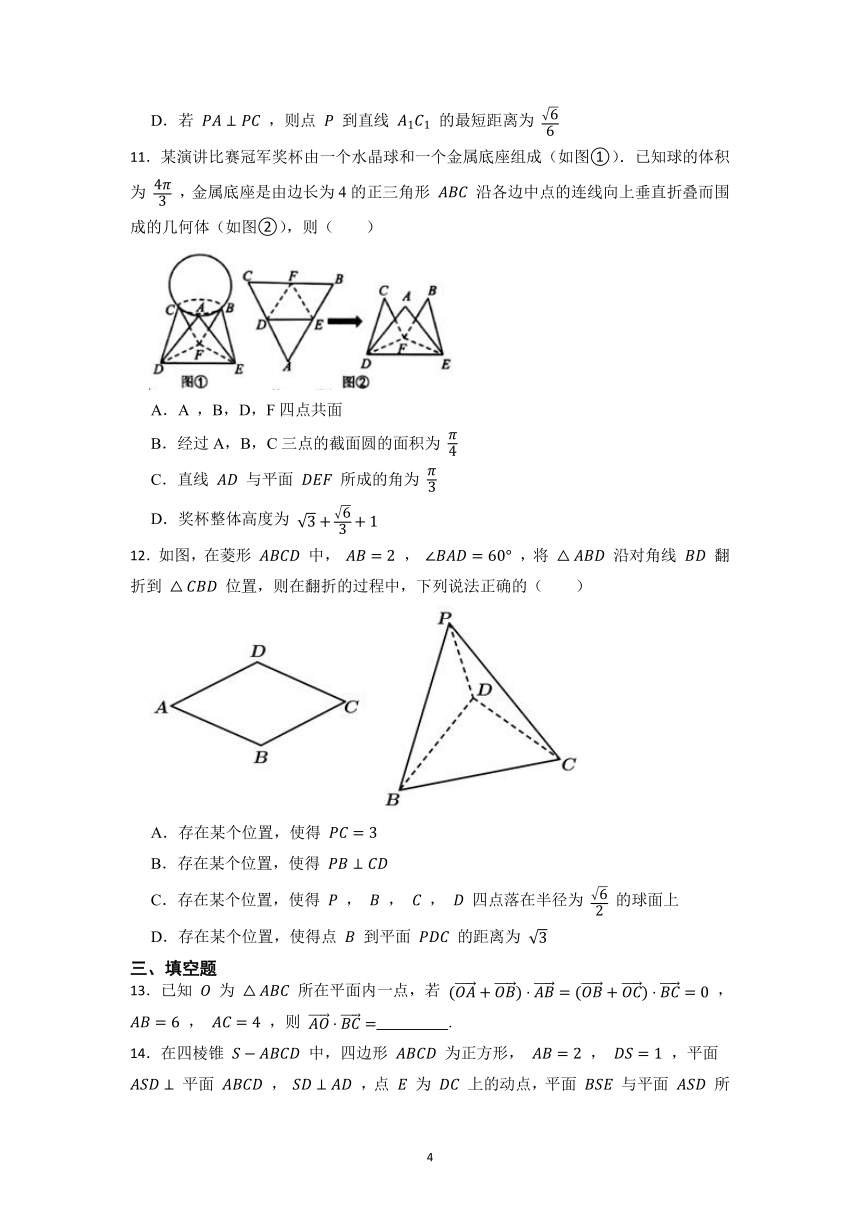
D.若 ,则点 到直线 的最短距离为
11.某演讲比赛冠军奖杯由一个水晶球和一个金属底座组成(如图①).已知球的体积为 ,金属底座是由边长为4的正三角形 沿各边中点的连线向上垂直折叠而围成的几何体(如图②),则( )
A.A ,B,D,F四点共面
B.经过A,B,C三点的截面圆的面积为
C.直线 与平面 所成的角为
D.奖杯整体高度为
12.如图,在菱形 中, , ,将 沿对角线 翻折到 位置,则在翻折的过程中,下列说法正确的( )
A.存在某个位置,使得
B.存在某个位置,使得
C.存在某个位置,使得 , , , 四点落在半径为 的球面上
D.存在某个位置,使得点 到平面 的距离为
三、填空题
13.已知 为 所在平面内一点,若 , , ,则 .
14.在四棱锥 中,四边形 为正方形, , ,平面 平面 , ,点 为 上的动点,平面 与平面 所成的二面角为 ( 为锐角),则当 取最小值时,三棱锥 的体积为 .
15.平面内一点 到直线 : 的距离为: .由此类比,空间中一点 到平面 : 的距离为 .
16.如图,已知棱长为2的正方体 中,点 在线段 上运动,给出下列结论:
①异面直线 与 所成的角范围为 ;
②平面 平面 ;
③点 到平面 的距离为定值 ;
④存在一点 ,使得直线 与平面 所成的角为 .
其中正确的结论是 .
四、解答题
17.如图,多面体 中, 平面 ,点 为 的中点,
(1)求证:平面 平面 ;
(2)求二面角 的大小.
18.如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为梯形,二面角P-AD-C为直二面角,且AB∥DC,AB⊥AD,AD=AB= DC,F为PC的中点.
(1)求证:BF∥平面PAD;
(2)求直线PC与平面PAB所成的角的余弦值.
19.在四棱锥 中,底面ABCD是矩形, 为BC的中点, .
(1)证明: 平面ABCD;
(2)若PC与平面PAD所成的角为30°,求二面角 的余弦值.
20.已知四棱锥 中,四边形 是菱形,且 , 为等边三角形,平面 平面 .
(1)求证: ;
(2)若点 是线段 上靠近 的三等分点,求直线 与平面 所成角的正弦值.
21.如图,三棱锥 的底面是等腰直角三角形,其中 , ,平面 平面 ,点 , , , 分别是 , , , 的中点.
(1)证明:平面 平面 ;
(2)当 与平面 所成的角为 时,求四棱锥 的体积.
22.如图,在四棱台 中,底面四边形 为菱形, , , 平面 .
(1)若点 是 的中点,求证: ;
(2)棱 上是否存在一点 ,使得二面角 的余弦值为 ?若存在,求线段 的长;若不存在,请说明理由.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】A,D
10.【答案】A,C,D
11.【答案】A,C,D
12.【答案】A,B,C
13.【答案】-10
14.【答案】
15.【答案】
16.【答案】②③
17.【答案】(1)取 中点 ,连接 ,
则 且 ,
又 且 ,
所以 ,即四边形 为平行四边形,
从而 ,
而 ,
所以 ,
平面 ,
所以 平面 ,
所以
且 ,
所以 平面 ,
所以 平面 平面 ,
所以平面 平面
(2)由(1)知,分别以 为 轴建立空间坐标系,
又 ,
所以 ,
所以平面 的一个法向量 ,
设平面 的法向量分别为 ,
所以 ,
即 ,
可得平面 的一个法向量为
所以二面角 为余弦值 ,
沂以二面角 的大小为 .
18.【答案】(1)证明:证明:如图所示,取 的中点 ,连接 , .
为 的中点, .
又 , 且 .
四边形 为平行四边形. .
又 平面 , 平面 , 平面 .
(2)解:取 的中点 ,连接 ,由 为正三角形, .
取 的中点 ,连接 , 四边形 为梯形,
. . 为二面角 的平面角.
又二面角 为直二面角, . .
以 为坐标原点, , , 所在直线分别为 轴, 轴, 轴,建立如图所示的空间直角坐标系:
设 ,则 , , , ,
故 , .
设平面 的一个法向量为 ,则
则可取 .
设直线 与平面 所成的角为 .
.
, .
故直线 与平面 所成的角的余弦值为 .
19.【答案】(1)证明:易知 ,
所以 ,故 ,即 ,
又 ,
所以 平面PAE,又 平面PAE,
所以 又 ,
所以 平面ABCD.
(2)由 平面平面ABCD,得 ,又 ,
所以 平面PAD,
所以 为PC与平面PAD所成的角,则 ,
在 中, ,所以 ,又 ,所以 .
以A为原点, 的方向分别为x轴、y轴、z轴的正方向,建立如图所示的空间直角坐标系,则 ,
,
设平面PDE的法向量为 ,
则
取 ,则 ,所以 ,
易知平面PAE的一个法向量为 ,
所以 ,
由图可知二面角 为锐角,
所以二面角 的余弦值为 .
20.【答案】(1)证明:取 的中点 ,连接 、 和 ,因为 为等边三角形,所以 ;又四边形 是菱形,且 ,所以 为等边三角形,所以 ;又 , 平面 , 平面 ,所以 平面 ,又 平面 ,所以 ;
(2)解:因为平面 平面 ,平面 平面 , , 平面 ,所以 平面 ;又 ,所以 、 、 两两垂直;以点 为坐标原点, 、 、 所在直线分别为 、 、 轴建立空间直角坐标系 ;不妨设 ,则 , , , ,0, , ,0, ;所以 , , , , , ;设平面 的一个法向量为 , , ,由 ,得 ,令 ,得 ,1, ,又 , , ,所以 , , ,又 , , ,所以 , , ,设直线 与平面 所成的角为 ,则 .
21.【答案】(1)证明:由题意可得, ,
点 , 分别是 , 的中点,
故 ∥AC,故 ,
平面 平面 ,交线为
故 平面
在平面 内,
故平面 平面 ;
(2)连结 ,由 ,点 是 的中点,可知 ,
再由平面 平面 ,可知 平面 ,
连结 ,可知 就是直线 与平面 所成的角,
于是 ,
因为 , 是 中点,故 ,
又平面 平面 ,故 平面 ,
即点 到平面 的距离为 .
点 是 中点,故点 到平面 的距离为 ,
即四棱锥 的体积为 .
22.【答案】(1)取 中点 ,连接 , , ,
因为四边形 为菱形,则 ,
∵ ,∴ 为等边三角形,
∵ 为 的中点,则 ,
∵ ,∴ ,
由于 平面 ,以点 为坐标原点,以 , , 所在直线分别为 轴、 轴、 轴建立空间直角坐标系,如图.
则 , , , , , , ,
, ,
∴ ,∴ ;
(2)假设点 存在,设点 的坐标为 ,其中 , , ,
设平面 的法向量为 ,则 即 ,
取 ,则 , ,所以, ,
平面 的一个法向量为 ,
所以, ,解得 ,
又由于二面角 为锐角,由图可知,点 在线段 上,
所以 ,即 .
因此,棱 上存在一点 ,使得二面角 的余弦值为 ,此时
(
1
)
一、单选题
1.已知平面 的一个法向量 ,点 在平面 内,则点 到平面 的距离为( )
A. B. C. D.
2.如图,在正三棱柱 中, ,则异面直线 与 所成角的余弦值是( )
A.0 B. C. D.
3.如图,直三棱柱 中, ,点P在棱 上,且三棱锥A-PBC的体积为4,则直线 与平面PBC所成角的正弦值等于( )
A. B. C. D.
4.三棱锥 中, 底面ABC, , ,D为AB的中点, ,则点D到面 的距离等于( )
A. B. C. D.
5.在正方体 中, , , 分别是棱 , , 的中点,下列说法错误的是( )
A. B. 与 是异面直线
C. , , , 四点共面 D.直线 与平面 相交
6.“阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美如图.将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形,六个面为正方形的“阿基米德多面体”,则异面直线AB与CD所成角的大小是( )
A.30° B.45° C.60° D.120°
7.在直三棱柱 中, 是 中点. , , , .则下列结论正确的是( )
A.点 到平面 的距离是
B.异面直线 与 的角的余弦值是
C.若 为侧面 (含边界)上一点,满足 平面 ,则线段 长的最小值是5.
D.过 , , 的截面是钝角三角形
8.如图,在正方体 中, 为线段 的中点, 为线段 上的动点,则直线 与直线 所成角正弦值的最小值为( )
A. B. C. D.
二、多选题
9.如图,正三棱柱 的底面边长为2,侧棱长为 , 为 的中点,则正确的结论有( )
A. 平面
B. 与平面 所成的角为
C.三棱锥 的体积为
D. 到平面 的距离为
10.正方体 棱长为 ,若 是空间异于 的一个动点,且 ,则下列正确的是( )
A. 平面
B.存在唯一一点 ,使
C.存在无数个点 ,使
D.若 ,则点 到直线 的最短距离为
11.某演讲比赛冠军奖杯由一个水晶球和一个金属底座组成(如图①).已知球的体积为 ,金属底座是由边长为4的正三角形 沿各边中点的连线向上垂直折叠而围成的几何体(如图②),则( )
A.A ,B,D,F四点共面
B.经过A,B,C三点的截面圆的面积为
C.直线 与平面 所成的角为
D.奖杯整体高度为
12.如图,在菱形 中, , ,将 沿对角线 翻折到 位置,则在翻折的过程中,下列说法正确的( )
A.存在某个位置,使得
B.存在某个位置,使得
C.存在某个位置,使得 , , , 四点落在半径为 的球面上
D.存在某个位置,使得点 到平面 的距离为
三、填空题
13.已知 为 所在平面内一点,若 , , ,则 .
14.在四棱锥 中,四边形 为正方形, , ,平面 平面 , ,点 为 上的动点,平面 与平面 所成的二面角为 ( 为锐角),则当 取最小值时,三棱锥 的体积为 .
15.平面内一点 到直线 : 的距离为: .由此类比,空间中一点 到平面 : 的距离为 .
16.如图,已知棱长为2的正方体 中,点 在线段 上运动,给出下列结论:
①异面直线 与 所成的角范围为 ;
②平面 平面 ;
③点 到平面 的距离为定值 ;
④存在一点 ,使得直线 与平面 所成的角为 .
其中正确的结论是 .
四、解答题
17.如图,多面体 中, 平面 ,点 为 的中点,
(1)求证:平面 平面 ;
(2)求二面角 的大小.
18.如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为梯形,二面角P-AD-C为直二面角,且AB∥DC,AB⊥AD,AD=AB= DC,F为PC的中点.
(1)求证:BF∥平面PAD;
(2)求直线PC与平面PAB所成的角的余弦值.
19.在四棱锥 中,底面ABCD是矩形, 为BC的中点, .
(1)证明: 平面ABCD;
(2)若PC与平面PAD所成的角为30°,求二面角 的余弦值.
20.已知四棱锥 中,四边形 是菱形,且 , 为等边三角形,平面 平面 .
(1)求证: ;
(2)若点 是线段 上靠近 的三等分点,求直线 与平面 所成角的正弦值.
21.如图,三棱锥 的底面是等腰直角三角形,其中 , ,平面 平面 ,点 , , , 分别是 , , , 的中点.
(1)证明:平面 平面 ;
(2)当 与平面 所成的角为 时,求四棱锥 的体积.
22.如图,在四棱台 中,底面四边形 为菱形, , , 平面 .
(1)若点 是 的中点,求证: ;
(2)棱 上是否存在一点 ,使得二面角 的余弦值为 ?若存在,求线段 的长;若不存在,请说明理由.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】A,D
10.【答案】A,C,D
11.【答案】A,C,D
12.【答案】A,B,C
13.【答案】-10
14.【答案】
15.【答案】
16.【答案】②③
17.【答案】(1)取 中点 ,连接 ,
则 且 ,
又 且 ,
所以 ,即四边形 为平行四边形,
从而 ,
而 ,
所以 ,
平面 ,
所以 平面 ,
所以
且 ,
所以 平面 ,
所以 平面 平面 ,
所以平面 平面
(2)由(1)知,分别以 为 轴建立空间坐标系,
又 ,
所以 ,
所以平面 的一个法向量 ,
设平面 的法向量分别为 ,
所以 ,
即 ,
可得平面 的一个法向量为
所以二面角 为余弦值 ,
沂以二面角 的大小为 .
18.【答案】(1)证明:证明:如图所示,取 的中点 ,连接 , .
为 的中点, .
又 , 且 .
四边形 为平行四边形. .
又 平面 , 平面 , 平面 .
(2)解:取 的中点 ,连接 ,由 为正三角形, .
取 的中点 ,连接 , 四边形 为梯形,
. . 为二面角 的平面角.
又二面角 为直二面角, . .
以 为坐标原点, , , 所在直线分别为 轴, 轴, 轴,建立如图所示的空间直角坐标系:
设 ,则 , , , ,
故 , .
设平面 的一个法向量为 ,则
则可取 .
设直线 与平面 所成的角为 .
.
, .
故直线 与平面 所成的角的余弦值为 .
19.【答案】(1)证明:易知 ,
所以 ,故 ,即 ,
又 ,
所以 平面PAE,又 平面PAE,
所以 又 ,
所以 平面ABCD.
(2)由 平面平面ABCD,得 ,又 ,
所以 平面PAD,
所以 为PC与平面PAD所成的角,则 ,
在 中, ,所以 ,又 ,所以 .
以A为原点, 的方向分别为x轴、y轴、z轴的正方向,建立如图所示的空间直角坐标系,则 ,
,
设平面PDE的法向量为 ,
则
取 ,则 ,所以 ,
易知平面PAE的一个法向量为 ,
所以 ,
由图可知二面角 为锐角,
所以二面角 的余弦值为 .
20.【答案】(1)证明:取 的中点 ,连接 、 和 ,因为 为等边三角形,所以 ;又四边形 是菱形,且 ,所以 为等边三角形,所以 ;又 , 平面 , 平面 ,所以 平面 ,又 平面 ,所以 ;
(2)解:因为平面 平面 ,平面 平面 , , 平面 ,所以 平面 ;又 ,所以 、 、 两两垂直;以点 为坐标原点, 、 、 所在直线分别为 、 、 轴建立空间直角坐标系 ;不妨设 ,则 , , , ,0, , ,0, ;所以 , , , , , ;设平面 的一个法向量为 , , ,由 ,得 ,令 ,得 ,1, ,又 , , ,所以 , , ,又 , , ,所以 , , ,设直线 与平面 所成的角为 ,则 .
21.【答案】(1)证明:由题意可得, ,
点 , 分别是 , 的中点,
故 ∥AC,故 ,
平面 平面 ,交线为
故 平面
在平面 内,
故平面 平面 ;
(2)连结 ,由 ,点 是 的中点,可知 ,
再由平面 平面 ,可知 平面 ,
连结 ,可知 就是直线 与平面 所成的角,
于是 ,
因为 , 是 中点,故 ,
又平面 平面 ,故 平面 ,
即点 到平面 的距离为 .
点 是 中点,故点 到平面 的距离为 ,
即四棱锥 的体积为 .
22.【答案】(1)取 中点 ,连接 , , ,
因为四边形 为菱形,则 ,
∵ ,∴ 为等边三角形,
∵ 为 的中点,则 ,
∵ ,∴ ,
由于 平面 ,以点 为坐标原点,以 , , 所在直线分别为 轴、 轴、 轴建立空间直角坐标系,如图.
则 , , , , , , ,
, ,
∴ ,∴ ;
(2)假设点 存在,设点 的坐标为 ,其中 , , ,
设平面 的法向量为 ,则 即 ,
取 ,则 , ,所以, ,
平面 的一个法向量为 ,
所以, ,解得 ,
又由于二面角 为锐角,由图可知,点 在线段 上,
所以 ,即 .
因此,棱 上存在一点 ,使得二面角 的余弦值为 ,此时
(
1
)
