人教版七年级上册 3.4.4分段计费问题与方案决策问题课件(共31张PPT)
文档属性
| 名称 | 人教版七年级上册 3.4.4分段计费问题与方案决策问题课件(共31张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 769.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 16:06:23 | ||
图片预览




文档简介
(共31张PPT)
第三章
一元一次方程
七年级数学人教版·上册
3.4.4分段计费问题与方案决策问题
授课人:XXXX
教学目标
1. 体会分类思想和方程思想在解决问题中的作用,
能够根据已知条件选择分类关键点对“电话计费
问题”进行整体分析,从而得出整体选择方案.
(重点、难点)
2. 进一步深化对数学建模方法的体验,增强应用
方程模型解决问题的意识和能力.(重点)
情景引入
新知探究
电话计费问题
一
互动探究
下表中有两种移动电话计费方式.
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
新知探究
想一想 你觉得哪种计费方式更省钱?
填填下面的表格,你有什么发现?
主叫时间(分) 100 150 250 300 350 450
方式一计费(元)
方式二计费(元)
58
58
83
95.5
108
133
88
88
88
88
88
107
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
哪种计费方式更省钱与“主叫时间有关”.
月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
新知探究
因此,考虑 t 的取值时,两个主叫限定时间 150 min和 350 min是不同时间范围的划分点.
计费时首先要看主叫是否超过限定时间,主叫不超过限定时间,月使用费一定;
主叫超过限定时间,超时部分加收超时费.
问题1 设一个月内移动电话主叫为 t min (t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
新知探究
当 t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
58+0.25(t-150)
88
88
108
58+0.25(t-150)
88+0.19(t-350)
新知探究
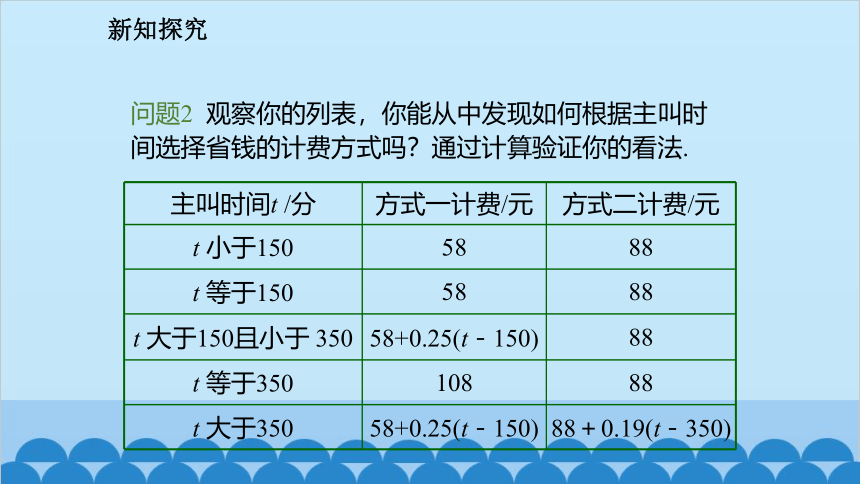
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题2 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
新知探究
主叫时间t /分 方式一计费/元 方式二计费/元
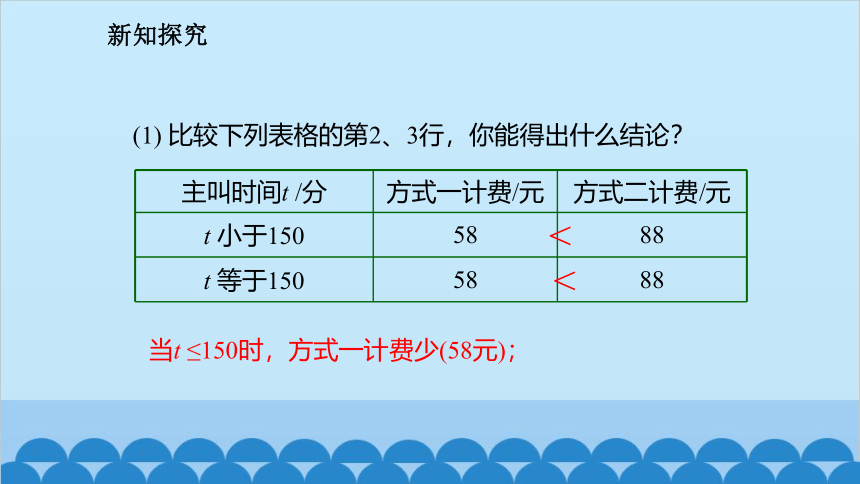
t 小于150 58 88
t 等于150 58 88
当t ≤150时,方式一计费少(58元);
(1) 比较下列表格的第2、3行,你能得出什么结论?
<
<
新知探究
主叫时间t /分 方式一计费/元 方式二计费/元
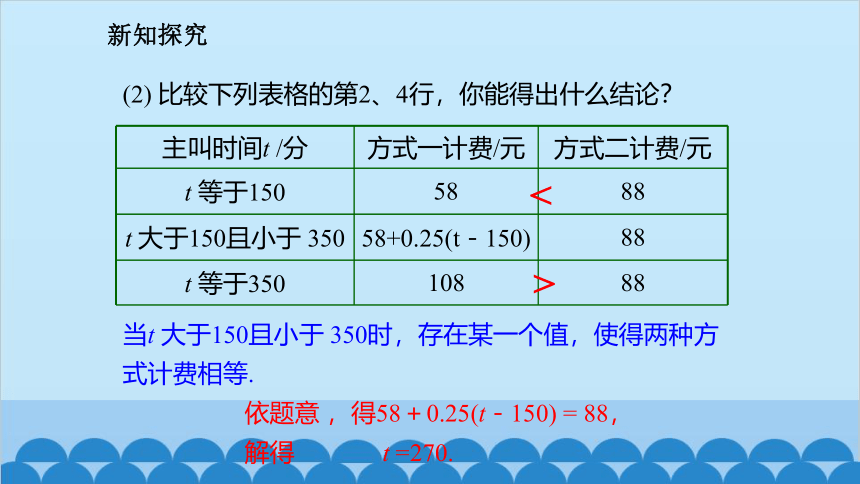
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
(2) 比较下列表格的第2、4行,你能得出什么结论?
>
<
当t 大于150且小于 350时,存在某一个值,使得两种方式计费相等.
依题意 ,得58+0.25(t-150) = 88,
解得 t =270.
新知探究
主叫时间t /分 方式一计费/元 方式二计费/元
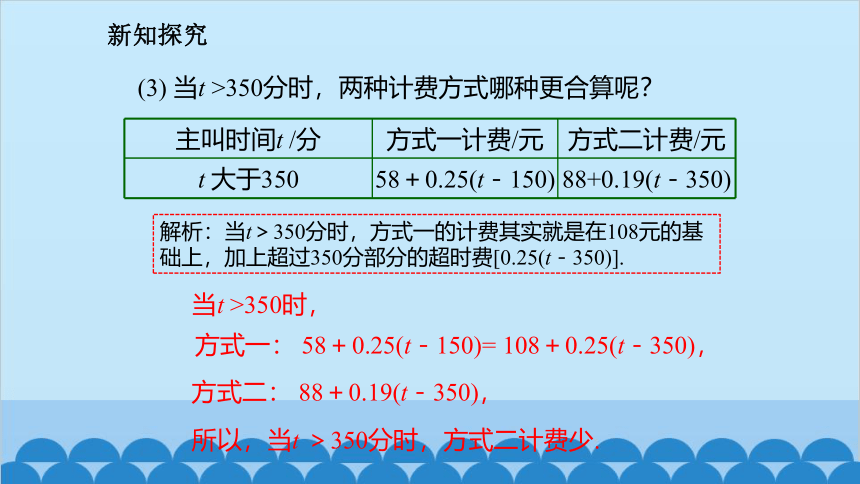
t 大于350 58+0.25(t-150) 88+0.19(t-350)
解析:当t>350分时,方式一的计费其实就是在108元的基础上,加上超过350分部分的超时费[0.25(t-350)].
(3) 当t >350分时,两种计费方式哪种更合算呢?
当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350),
方式二: 88+0.19(t-350),
所以,当t >350分时,方式二计费少.
新知探究
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
270
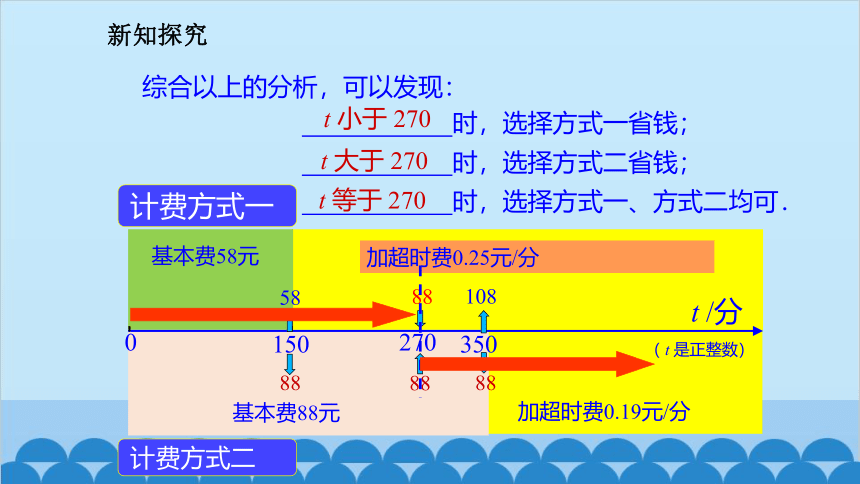
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱;
时,选择方式一、方式二均可.
t 小于 270
t 大于 270
t 等于 270
新知探究
(1)回顾问题的解决过程,谈谈你的收获.
(2)解决本题的过程中你觉得最难突破的步骤是哪些?本题中运用了哪些方法突破这些难点?
(3)电话计费问题的解决过程中运用一元一次方程解决了什么问题?
新知探究
列表分析
借助数轴
审题
分类讨论
更优惠
费用相同
列方程
用未知数表示费用
设未知数
如何比较两个代数式的大小?
要找不等关系先找等量关系
新知探究
例 小明和小强为了买同一种火车模型,决定从春节开始攒钱.小明原有200元,以后每月存50元;小强原有150元,以后每月存60元.设两人攒钱的月数为x(个)(x为整数).
(1)根据题意,填写下表:
攒钱的月数/个 3 6 … x
小明攒钱的总数/元 350 …
小强攒钱的总数/元 510 …
330
500
200+50x
150+60x
新知探究
(2)在几个月后小明与小强攒钱的总数相同?此时他们各有多少钱?
(2) 根据题意,得200+50x=150+60x,
解得x=5,
所以150+60x=450.
答:在5个月后小明与小强攒钱的总数相同,此时每人有450元钱.
新知探究
(3)若这种火车模型的价格为780元,他们谁能够先买到该模型?
(3) 根据题意,由200+50x=780,解得x=11.6,故小明在12个月后攒钱的总数超过780元.
由150+60x=780,解得x=10.5,
故小强在11个月后攒钱的总数超过780元.
所以小强能够先买到该模型.
新知探究
方法总结:解决此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型,分类讨论,从而得出整体选择方案.
新知探究
做一做
移动公司推出两种智能手机上网流量包:
月使用费(元) 含上网流量(M) 流量超出部分(元/M)
A种 30 320 0.2
B种 50 550 0.1
如何选择流量包更划算?
新知探究
解:设一个月内使用的流量为 x M.根据题意可知当x
在不同范围内取值时,两种流量包计费如下表:
使用流量 x(M) A种计费(元) B种计费(元)
x小于等于320 30 50
x大于320且小于550 30+0.2(x-320) 50
x等于550 76 50
x大于550 30+0.2(x-320) 50+0.1(x-550)
① 当 x ≤ 320 时,流量包A 计费少(30元);
② 当 320<x<420 时,流量包A 计费少(<50元);
③ 当 x = 420时,两种流量包计费相等,都是50元;
新知探究
④当 420<x≤550 时,流量包B 计费少(50元);
⑤ 当 x = 550 时,流量包B 计费少(50元);
⑥ 当 x>550 时,流量包B 计费少.
综上所述,
当月使用流量小于 420 M 时,选择流量包A 划算;
当月使用流量等于 420 M 时,两种流量包费用一样;
当月使用流量大于 420 M 时,选择流量包B 划算.
巩固练习
1.小明所在城市的“阶梯水价”收费办法:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元.小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44
B.5x+4(x-2)=44
C.9(x+2)=44
D.9(x+2)-4×2=44
A
巩固练习
2. 某市为鼓励居民节约用水,对自来水用户按分段
计费方式收取水费:若每户每月用水不超过 7m3,
则按 2 元/m3 收费;若每户每月用水超过 7 m3,
则超过的部分按 3元/m3 收费. 如果某户居民去年
12月缴纳了 53 元水费,那么这户居民去年12月
的用水量为_______m3.
20
课堂小结
1. 解决电话计费问题需要明确“哪种计费方式更省
钱”与“主叫时间”有关.
2. 方案决策问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
课堂小测
1. 某市生活拨号上网有两种收费方式,用户可以任选
其一. A计时制:0.05 元/分钟;B包月制:60 元/月
(限一部个人住宅电话上网). 此外,两种上网
方式都得加收通信费 0.02 元/分钟.
(1) 某用户某月上网时间为x小时,请分别写出两种
收费方式下该用户应该支付的费用;
(2) 你认为采用哪种方式比较合算?
解:(1) 采用计时制:(0.05+0.02)×60x=4.2x,
采用包月制:60+0.02×60x=60+1.2x;
课堂小测
(2) 由 4.2x = 60+1.2x,得 x=20. 又由题意可知,上
网时间越长,采用包月制越合算.因此,
当 0 < x < 20 时,采用计时制合算;
当 x=20 时,两种方式费用相同;
当 x > 20 时,采用包月制合算.
课堂小测
2. 用A4纸在某复印社复印文件,复印页数不超过20
时,每页收费0.12元;复印页数超过20时,超过部
分每页收费0.09元. 在某图书馆复印同样的文件,
不论复印多少页,每页收费0.1元. 问:如何根据
复印的页数选择复印的地点使总价格比较便宜
(复印的页数不为零)?
课堂小测
复印页数x 复印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:设复印页数为x,依题意,列表如下:
① 当 x <20 时,0.12x 大于 0.1x 恒成立,图书馆价
格便宜;
② 当 x = 20 时,图书馆价格便宜;
课堂小测
③ 当 x 大于20时,依题意得
2.4+0.09(x-20) = 0.1x.
解得 x = 60
所以,当x大于20且小于60时,图书馆价格便宜;
当x等于60时,两者价格相同;
当x大于60时,复印社价格便宜.
综上所述,当 x 小于60页时,图书馆价格便宜;
当 x 等于60时,两者价格相同;
当 x 大于60时,复印社价格便宜.
课堂小测
3. 小明可以到甲或乙商店购买练习本.已知两商店的标
价都是每本1元,甲商店的优惠方法是购买10本
以上时,从第11本开始按标价的70%出售;乙商店
的优惠方法是从第一本开始就按标价的80%出售.
(1) 小明要买20本时,到哪家商店购买省钱;
(2) 买多少本时,到两个商店花的钱一样多;
(3) 小明现有29.6元钱,最多可买多少本练习本.
课堂小测
解:(1)甲店需付款10+10×0.7=17元;乙商店需付款20×0.8=16元,
17元>16元,故到乙商店购买省钱.
(2)设买x本时到两个商店付的钱一样多.
依题意列方程:10+(x-10)×70%=80%x,
解得x=30.
故买30本时到两个商店付的钱一样多.
(3)设最多可买a本,
则甲商店10+(a-10)×70%=29.6,解得a=38;
乙商店80%a=29.6,
解得a=37.
38>37,故最多可买38本.
第三章
一元一次方程
七年级数学人教版·上册
3.4.4分段计费问题与方案决策问题
授课人:XXXX
教学目标
1. 体会分类思想和方程思想在解决问题中的作用,
能够根据已知条件选择分类关键点对“电话计费
问题”进行整体分析,从而得出整体选择方案.
(重点、难点)
2. 进一步深化对数学建模方法的体验,增强应用
方程模型解决问题的意识和能力.(重点)
情景引入
新知探究
电话计费问题
一
互动探究
下表中有两种移动电话计费方式.
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
新知探究
想一想 你觉得哪种计费方式更省钱?
填填下面的表格,你有什么发现?
主叫时间(分) 100 150 250 300 350 450
方式一计费(元)
方式二计费(元)
58
58
83
95.5
108
133
88
88
88
88
88
107
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
哪种计费方式更省钱与“主叫时间有关”.
月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
新知探究
因此,考虑 t 的取值时,两个主叫限定时间 150 min和 350 min是不同时间范围的划分点.
计费时首先要看主叫是否超过限定时间,主叫不超过限定时间,月使用费一定;
主叫超过限定时间,超时部分加收超时费.
问题1 设一个月内移动电话主叫为 t min (t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
新知探究
当 t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
58+0.25(t-150)
88
88
108
58+0.25(t-150)
88+0.19(t-350)
新知探究
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题2 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
新知探究
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
当t ≤150时,方式一计费少(58元);
(1) 比较下列表格的第2、3行,你能得出什么结论?
<
<
新知探究
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
(2) 比较下列表格的第2、4行,你能得出什么结论?
>
<
当t 大于150且小于 350时,存在某一个值,使得两种方式计费相等.
依题意 ,得58+0.25(t-150) = 88,
解得 t =270.
新知探究
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
解析:当t>350分时,方式一的计费其实就是在108元的基础上,加上超过350分部分的超时费[0.25(t-350)].
(3) 当t >350分时,两种计费方式哪种更合算呢?
当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350),
方式二: 88+0.19(t-350),
所以,当t >350分时,方式二计费少.
新知探究
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
270
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱;
时,选择方式一、方式二均可.
t 小于 270
t 大于 270
t 等于 270
新知探究
(1)回顾问题的解决过程,谈谈你的收获.
(2)解决本题的过程中你觉得最难突破的步骤是哪些?本题中运用了哪些方法突破这些难点?
(3)电话计费问题的解决过程中运用一元一次方程解决了什么问题?
新知探究
列表分析
借助数轴
审题
分类讨论
更优惠
费用相同
列方程
用未知数表示费用
设未知数
如何比较两个代数式的大小?
要找不等关系先找等量关系
新知探究
例 小明和小强为了买同一种火车模型,决定从春节开始攒钱.小明原有200元,以后每月存50元;小强原有150元,以后每月存60元.设两人攒钱的月数为x(个)(x为整数).
(1)根据题意,填写下表:
攒钱的月数/个 3 6 … x
小明攒钱的总数/元 350 …
小强攒钱的总数/元 510 …
330
500
200+50x
150+60x
新知探究
(2)在几个月后小明与小强攒钱的总数相同?此时他们各有多少钱?
(2) 根据题意,得200+50x=150+60x,
解得x=5,
所以150+60x=450.
答:在5个月后小明与小强攒钱的总数相同,此时每人有450元钱.
新知探究
(3)若这种火车模型的价格为780元,他们谁能够先买到该模型?
(3) 根据题意,由200+50x=780,解得x=11.6,故小明在12个月后攒钱的总数超过780元.
由150+60x=780,解得x=10.5,
故小强在11个月后攒钱的总数超过780元.
所以小强能够先买到该模型.
新知探究
方法总结:解决此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型,分类讨论,从而得出整体选择方案.
新知探究
做一做
移动公司推出两种智能手机上网流量包:
月使用费(元) 含上网流量(M) 流量超出部分(元/M)
A种 30 320 0.2
B种 50 550 0.1
如何选择流量包更划算?
新知探究
解:设一个月内使用的流量为 x M.根据题意可知当x
在不同范围内取值时,两种流量包计费如下表:
使用流量 x(M) A种计费(元) B种计费(元)
x小于等于320 30 50
x大于320且小于550 30+0.2(x-320) 50
x等于550 76 50
x大于550 30+0.2(x-320) 50+0.1(x-550)
① 当 x ≤ 320 时,流量包A 计费少(30元);
② 当 320<x<420 时,流量包A 计费少(<50元);
③ 当 x = 420时,两种流量包计费相等,都是50元;
新知探究
④当 420<x≤550 时,流量包B 计费少(50元);
⑤ 当 x = 550 时,流量包B 计费少(50元);
⑥ 当 x>550 时,流量包B 计费少.
综上所述,
当月使用流量小于 420 M 时,选择流量包A 划算;
当月使用流量等于 420 M 时,两种流量包费用一样;
当月使用流量大于 420 M 时,选择流量包B 划算.
巩固练习
1.小明所在城市的“阶梯水价”收费办法:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元.小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44
B.5x+4(x-2)=44
C.9(x+2)=44
D.9(x+2)-4×2=44
A
巩固练习
2. 某市为鼓励居民节约用水,对自来水用户按分段
计费方式收取水费:若每户每月用水不超过 7m3,
则按 2 元/m3 收费;若每户每月用水超过 7 m3,
则超过的部分按 3元/m3 收费. 如果某户居民去年
12月缴纳了 53 元水费,那么这户居民去年12月
的用水量为_______m3.
20
课堂小结
1. 解决电话计费问题需要明确“哪种计费方式更省
钱”与“主叫时间”有关.
2. 方案决策问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
课堂小测
1. 某市生活拨号上网有两种收费方式,用户可以任选
其一. A计时制:0.05 元/分钟;B包月制:60 元/月
(限一部个人住宅电话上网). 此外,两种上网
方式都得加收通信费 0.02 元/分钟.
(1) 某用户某月上网时间为x小时,请分别写出两种
收费方式下该用户应该支付的费用;
(2) 你认为采用哪种方式比较合算?
解:(1) 采用计时制:(0.05+0.02)×60x=4.2x,
采用包月制:60+0.02×60x=60+1.2x;
课堂小测
(2) 由 4.2x = 60+1.2x,得 x=20. 又由题意可知,上
网时间越长,采用包月制越合算.因此,
当 0 < x < 20 时,采用计时制合算;
当 x=20 时,两种方式费用相同;
当 x > 20 时,采用包月制合算.
课堂小测
2. 用A4纸在某复印社复印文件,复印页数不超过20
时,每页收费0.12元;复印页数超过20时,超过部
分每页收费0.09元. 在某图书馆复印同样的文件,
不论复印多少页,每页收费0.1元. 问:如何根据
复印的页数选择复印的地点使总价格比较便宜
(复印的页数不为零)?
课堂小测
复印页数x 复印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:设复印页数为x,依题意,列表如下:
① 当 x <20 时,0.12x 大于 0.1x 恒成立,图书馆价
格便宜;
② 当 x = 20 时,图书馆价格便宜;
课堂小测
③ 当 x 大于20时,依题意得
2.4+0.09(x-20) = 0.1x.
解得 x = 60
所以,当x大于20且小于60时,图书馆价格便宜;
当x等于60时,两者价格相同;
当x大于60时,复印社价格便宜.
综上所述,当 x 小于60页时,图书馆价格便宜;
当 x 等于60时,两者价格相同;
当 x 大于60时,复印社价格便宜.
课堂小测
3. 小明可以到甲或乙商店购买练习本.已知两商店的标
价都是每本1元,甲商店的优惠方法是购买10本
以上时,从第11本开始按标价的70%出售;乙商店
的优惠方法是从第一本开始就按标价的80%出售.
(1) 小明要买20本时,到哪家商店购买省钱;
(2) 买多少本时,到两个商店花的钱一样多;
(3) 小明现有29.6元钱,最多可买多少本练习本.
课堂小测
解:(1)甲店需付款10+10×0.7=17元;乙商店需付款20×0.8=16元,
17元>16元,故到乙商店购买省钱.
(2)设买x本时到两个商店付的钱一样多.
依题意列方程:10+(x-10)×70%=80%x,
解得x=30.
故买30本时到两个商店付的钱一样多.
(3)设最多可买a本,
则甲商店10+(a-10)×70%=29.6,解得a=38;
乙商店80%a=29.6,
解得a=37.
38>37,故最多可买38本.
