湘教版八年级上册第2章 三角形 复习课件(共37张PPT)
文档属性
| 名称 | 湘教版八年级上册第2章 三角形 复习课件(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 771.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 17:15:52 | ||
图片预览









文档简介
(共37张PPT)
第2章 三角形
第2章 复习课
1.理解三角形的基本概念与边、角关系.
2.知道证明命题的依据,能用几何语言写出一个命题的证明过程.
3.知道等腰三角形、垂直平分线的性质,会用尺规作图.
4.知道全等图形的性质,会用几种不同的方法判定两个三角形全等.
◎重点:证明两个三角形全等,解决相关几何问题.
◎难点:尺规作图的依据与实际意义.
1.由不在 同一条直线上 的三条线段 首尾顺次 相连接所组成的图形叫作三角形.
2.三角形的三边关系:三角形任意两边之和 大于 第三边,任意两边之差 小于 第三边(填“大于”或“小于” ).
3. 正确 的命题叫真命题, 错误 的命题叫假命题;假命题可以通过举 反例 说明.
同一条直线上
首尾顺次
大于
小于
正确
错误
反例
4.每个命题都由 题设 和 结论 两部分组成,若将两者交换位置,得到的新命题就是原命题的 逆命题 .
5.三角形的内角和等于 180° ,三角形的一个外角等于 与它不相邻的两个内角的和 ,三角形的一个外角 大于 与它不相邻的任何一个内角.
6.能完全重合的两个图形叫作 全等图形 ,全等图形的对应边 相等 ,对应角 相等 .
题设
结论
逆命题
180°
与它不相邻的两个内角的和
大于
全等图形
相等
相等
7.判定两个三角形全等的方法有 SAS、ASA、AAS、SSS , SSA、AAA 无法判定两个三角形全等.
SAS、ASA、AAS、SSS
SSA、AAA
三角形的边角关系
1.在三角形中,最多有 3 个锐角,至少有 2 个锐角,最多有 1 个钝角(或直角).
2.已知一个三角形两边长分别为2 cm和6 cm,则第三边的长可以是 答案不唯一,如5、6等 cm.(写出一个符合条件的答案)
方法归纳交流 已知三角形的两边,已知两边的 差 <三角形的第三边<已知两边的 和 .
3
2
1
答案不唯一,如5、6等
差
和
三角形的角平分线、中线和高
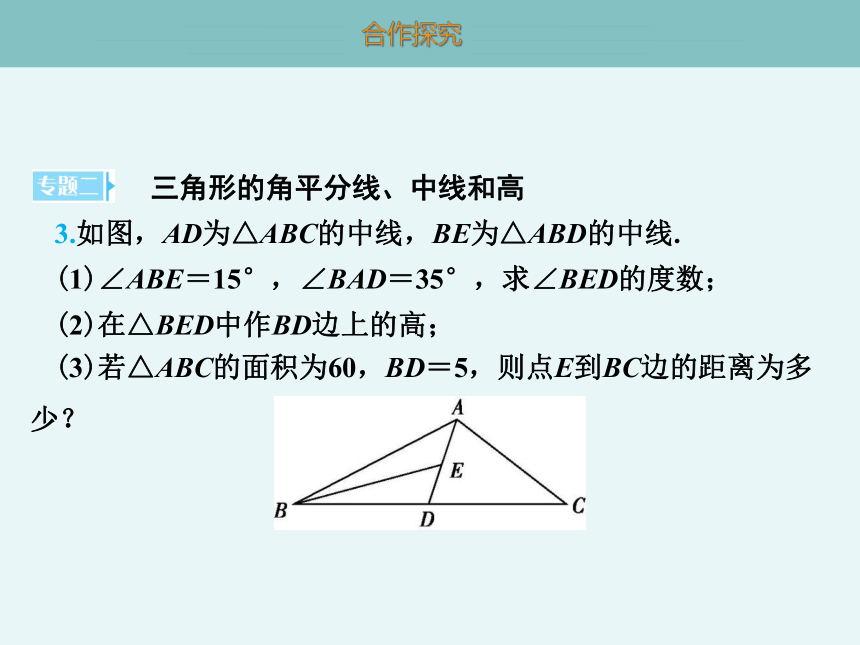
3.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
解:(1)∵∠BED是△ABE的一个外角,
∴∠BED=∠ABE+∠BAD=15°+35°=50°.
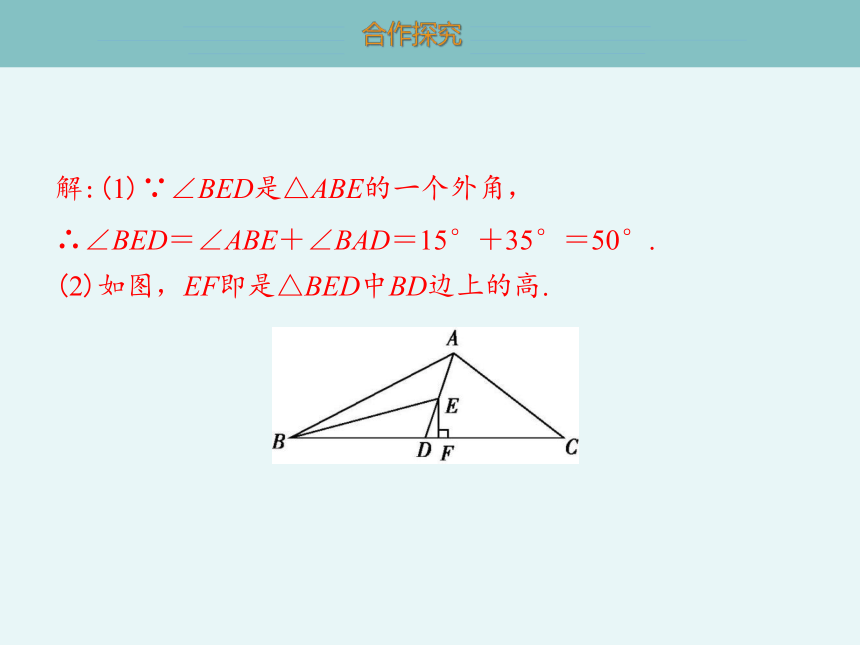
(2)如图,EF即是△BED中BD边上的高.
(3)∵AD为△ABC的中线,BE为△ABD的中线,
∴S△BED=S△ABC=×60=15;
∵BD=5,∴EF=2S△BED÷BD=2×15÷5=6,
即点E到BC边的距离为6.
等腰三角形
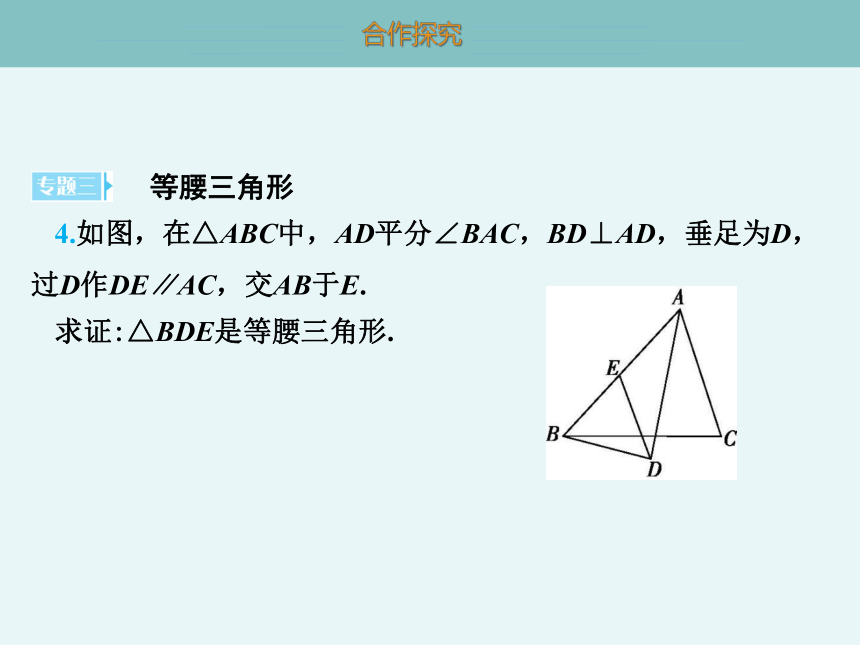
4.如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.
求证:△BDE是等腰三角形.
证明:∵AD平分∠BAC,DE∥AC,
∴∠EAD=∠CAD,∠EDA=∠CAD,
∴∠EAD=∠EDA,
∵BD⊥AD,
∴∠EBD+∠EAD=∠BDE+∠EDA,
∴∠EBD=∠BDE,
∴DE=BE,
∴△BDE是等腰三角形.
线段的垂直平分线
5.如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15 cm,△BCE的周长等于25 cm.
(1)求BC的长;
(2)若∠A=36°,并且AB=AC.求证:BC=BE.
(1)解:∵AB的垂直平分线MN交AB于点D,
∴AE=BE,
∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC,
∵AC=15 cm,
∴BC=25-15=10 cm.
(1)解:∵AB的垂直平分线MN交AB于点D,
(2)证明:∵∠A=36°,AB=AC,
∴∠C=(180°-∠A)=(180°-36°)=72°,
∵AB的垂直平分线MN交AB于点D,
∴AE=BE,∴∠ABE=∠A,
由三角形的外角性质得,∠BEC=∠A+∠ABE=36°+36°=72°,
∴∠BEC=∠C,∴BC=BE.
全等三角形的判定
6.如图,△ABC、△A1B1C1均为锐角三角形,AB=A1B1 ,BC=B1C1,∠C=∠C1.求证:△ABC≌△A1B1C1.
证明:本题解法不唯一.
分别过点B、B1作BD⊥CA于D,B1D1⊥C1A1于D1,
则∠BDC=∠B1D1C1=90°.
∵BC=B1C1,∠C=∠C1,∴△BCD≌△B1C1D1,
∴CD=C1D1,BD=B1D1.
又∵AB=A1B1 ,∠ADB=∠A1D1B1=90°,∴△ADB≌△A1D1B1,∴AD=A1D1,
∴CA=C1A1,又∵ AB=A1B1 ,BC=B1C1,∴△ABC≌△A1B1C1(SSS).
方法归纳交流 在证明过程中,有些全等条件需要 证明 得到,三角形全等是证明 线段相等 、 角相等 、直线平行和垂直的常用方法.
证明
线段相等
角相等
1下列命题中是真命题的是 ( C )
A.两个锐角之和为钝角
B.两个锐角之和为锐角
C.钝角大于它的补角
D.锐角小于它的余角
C
2下列四个图形中,线段BE是△ABC的高的是( D )
D
3如果三角形的三个内角的度数比是2∶3∶4,则它是 ( A )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角或直角三角形
4现有四条钢线,长度分别为(单位: cm)7、6、3、2,从中取出三根连成一个三角形,这三根的长度可以为 答案不唯一,如7,6,3 .(写出一种即可)
A
答案不唯一,如7,
6,3
5在△ABC和△A'B'C'中,AB=A'B',AC=A'C',∠C=60°,AD,A'D'分别为BC,B'C'边上的高,且AD=A'D',则∠C'的度数为 ( D )
A.60° B.120°
C.60°或30° D.60° 或120°
D
6如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= 70° .
70°
7如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于 20° .
20°
8如图,AD、AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?
解:∵AD平分∠CAB,∴∠1=∠2=∠CAB,
又∵AE平分∠CAF,∴∠3=∠4=∠CAF,
∵∠CAB+∠CAF=180°,∴∠1+∠3=(∠CAB+∠CAF)=×180°=90°,
∴AD⊥AE.
9已知△ABC≌△A'B'C',且△A'B'C'的面积等于12,如果BC=6,求BC边上的高AD.
解:∵△ABC≌△A'B'C',∴S△ABC=S△A'B'C',
∵△A'B'C'的面积等于12,
∴△ABC的面积等于12.
∵S△ABC=BC·AD,∴AD=12×2÷6=4.故BC边上的高AD为4.
(2)求证:DE=EC.
10如图,在Rt△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E.
(1)求证:AE=2CE;
证明:(1)如图,连接BE.
∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=90°-∠A=60°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE.
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE.
(2)∵BE=AE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABE=30°,
∵DE⊥AB,∠C=90°,
∴DE=CE.
11如图,在等边△ABC中,其边长为1,D是BC的中点,点E,F分别在AB,AC边上,且∠EDF=120°.
(1)写出DE与DF的数量关系,并证明.
(2)若BE,DE,CF能围成一个三角形,求出这个三角形最大内角的度数.(要求:写出思路,画出图形,直接给出结果即可)
(1)结论:DE=DF.
证明:如图1,连接AD,作DN⊥AB,DM⊥AC,垂足分别为N、M.
∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∵BD=DC,
∴∠BAD=∠CAD,
∴DN=DM,
∵∠EDF=120°,
∴∠EDF+∠BAC=180°,∠AED+AFD=180°,
∵∠AED+∠DEN=180°,
∴∠DFM=∠DEN.
在△DNE和△DMF中,
∴△DNE≌△DMF,
∴DE=DF.
(2)最大内角为120°.
证明:如图2中,延长FD到M使得DF=DM,连接BM,EM.
在△DFC和△DMB中,
∴△DFC≌△DMB,
∴∠C=∠MBD=60°,BM=CF,
∵DE=DF=DM,∠EDM=180°-∠EDF=60°,
∴△EDM是等边三角形,
∴EM=DE,
∴EB、ED、CF能围成△EBM,
最大内角∠EBM=∠EBC+∠DBM=60°+60°=120°.
第2章 三角形
第2章 复习课
1.理解三角形的基本概念与边、角关系.
2.知道证明命题的依据,能用几何语言写出一个命题的证明过程.
3.知道等腰三角形、垂直平分线的性质,会用尺规作图.
4.知道全等图形的性质,会用几种不同的方法判定两个三角形全等.
◎重点:证明两个三角形全等,解决相关几何问题.
◎难点:尺规作图的依据与实际意义.
1.由不在 同一条直线上 的三条线段 首尾顺次 相连接所组成的图形叫作三角形.
2.三角形的三边关系:三角形任意两边之和 大于 第三边,任意两边之差 小于 第三边(填“大于”或“小于” ).
3. 正确 的命题叫真命题, 错误 的命题叫假命题;假命题可以通过举 反例 说明.
同一条直线上
首尾顺次
大于
小于
正确
错误
反例
4.每个命题都由 题设 和 结论 两部分组成,若将两者交换位置,得到的新命题就是原命题的 逆命题 .
5.三角形的内角和等于 180° ,三角形的一个外角等于 与它不相邻的两个内角的和 ,三角形的一个外角 大于 与它不相邻的任何一个内角.
6.能完全重合的两个图形叫作 全等图形 ,全等图形的对应边 相等 ,对应角 相等 .
题设
结论
逆命题
180°
与它不相邻的两个内角的和
大于
全等图形
相等
相等
7.判定两个三角形全等的方法有 SAS、ASA、AAS、SSS , SSA、AAA 无法判定两个三角形全等.
SAS、ASA、AAS、SSS
SSA、AAA
三角形的边角关系
1.在三角形中,最多有 3 个锐角,至少有 2 个锐角,最多有 1 个钝角(或直角).
2.已知一个三角形两边长分别为2 cm和6 cm,则第三边的长可以是 答案不唯一,如5、6等 cm.(写出一个符合条件的答案)
方法归纳交流 已知三角形的两边,已知两边的 差 <三角形的第三边<已知两边的 和 .
3
2
1
答案不唯一,如5、6等
差
和
三角形的角平分线、中线和高
3.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
解:(1)∵∠BED是△ABE的一个外角,
∴∠BED=∠ABE+∠BAD=15°+35°=50°.
(2)如图,EF即是△BED中BD边上的高.
(3)∵AD为△ABC的中线,BE为△ABD的中线,
∴S△BED=S△ABC=×60=15;
∵BD=5,∴EF=2S△BED÷BD=2×15÷5=6,
即点E到BC边的距离为6.
等腰三角形
4.如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.
求证:△BDE是等腰三角形.
证明:∵AD平分∠BAC,DE∥AC,
∴∠EAD=∠CAD,∠EDA=∠CAD,
∴∠EAD=∠EDA,
∵BD⊥AD,
∴∠EBD+∠EAD=∠BDE+∠EDA,
∴∠EBD=∠BDE,
∴DE=BE,
∴△BDE是等腰三角形.
线段的垂直平分线
5.如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15 cm,△BCE的周长等于25 cm.
(1)求BC的长;
(2)若∠A=36°,并且AB=AC.求证:BC=BE.
(1)解:∵AB的垂直平分线MN交AB于点D,
∴AE=BE,
∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC,
∵AC=15 cm,
∴BC=25-15=10 cm.
(1)解:∵AB的垂直平分线MN交AB于点D,
(2)证明:∵∠A=36°,AB=AC,
∴∠C=(180°-∠A)=(180°-36°)=72°,
∵AB的垂直平分线MN交AB于点D,
∴AE=BE,∴∠ABE=∠A,
由三角形的外角性质得,∠BEC=∠A+∠ABE=36°+36°=72°,
∴∠BEC=∠C,∴BC=BE.
全等三角形的判定
6.如图,△ABC、△A1B1C1均为锐角三角形,AB=A1B1 ,BC=B1C1,∠C=∠C1.求证:△ABC≌△A1B1C1.
证明:本题解法不唯一.
分别过点B、B1作BD⊥CA于D,B1D1⊥C1A1于D1,
则∠BDC=∠B1D1C1=90°.
∵BC=B1C1,∠C=∠C1,∴△BCD≌△B1C1D1,
∴CD=C1D1,BD=B1D1.
又∵AB=A1B1 ,∠ADB=∠A1D1B1=90°,∴△ADB≌△A1D1B1,∴AD=A1D1,
∴CA=C1A1,又∵ AB=A1B1 ,BC=B1C1,∴△ABC≌△A1B1C1(SSS).
方法归纳交流 在证明过程中,有些全等条件需要 证明 得到,三角形全等是证明 线段相等 、 角相等 、直线平行和垂直的常用方法.
证明
线段相等
角相等
1下列命题中是真命题的是 ( C )
A.两个锐角之和为钝角
B.两个锐角之和为锐角
C.钝角大于它的补角
D.锐角小于它的余角
C
2下列四个图形中,线段BE是△ABC的高的是( D )
D
3如果三角形的三个内角的度数比是2∶3∶4,则它是 ( A )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角或直角三角形
4现有四条钢线,长度分别为(单位: cm)7、6、3、2,从中取出三根连成一个三角形,这三根的长度可以为 答案不唯一,如7,6,3 .(写出一种即可)
A
答案不唯一,如7,
6,3
5在△ABC和△A'B'C'中,AB=A'B',AC=A'C',∠C=60°,AD,A'D'分别为BC,B'C'边上的高,且AD=A'D',则∠C'的度数为 ( D )
A.60° B.120°
C.60°或30° D.60° 或120°
D
6如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= 70° .
70°
7如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于 20° .
20°
8如图,AD、AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?
解:∵AD平分∠CAB,∴∠1=∠2=∠CAB,
又∵AE平分∠CAF,∴∠3=∠4=∠CAF,
∵∠CAB+∠CAF=180°,∴∠1+∠3=(∠CAB+∠CAF)=×180°=90°,
∴AD⊥AE.
9已知△ABC≌△A'B'C',且△A'B'C'的面积等于12,如果BC=6,求BC边上的高AD.
解:∵△ABC≌△A'B'C',∴S△ABC=S△A'B'C',
∵△A'B'C'的面积等于12,
∴△ABC的面积等于12.
∵S△ABC=BC·AD,∴AD=12×2÷6=4.故BC边上的高AD为4.
(2)求证:DE=EC.
10如图,在Rt△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E.
(1)求证:AE=2CE;
证明:(1)如图,连接BE.
∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=90°-∠A=60°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE.
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE.
(2)∵BE=AE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABE=30°,
∵DE⊥AB,∠C=90°,
∴DE=CE.
11如图,在等边△ABC中,其边长为1,D是BC的中点,点E,F分别在AB,AC边上,且∠EDF=120°.
(1)写出DE与DF的数量关系,并证明.
(2)若BE,DE,CF能围成一个三角形,求出这个三角形最大内角的度数.(要求:写出思路,画出图形,直接给出结果即可)
(1)结论:DE=DF.
证明:如图1,连接AD,作DN⊥AB,DM⊥AC,垂足分别为N、M.
∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∵BD=DC,
∴∠BAD=∠CAD,
∴DN=DM,
∵∠EDF=120°,
∴∠EDF+∠BAC=180°,∠AED+AFD=180°,
∵∠AED+∠DEN=180°,
∴∠DFM=∠DEN.
在△DNE和△DMF中,
∴△DNE≌△DMF,
∴DE=DF.
(2)最大内角为120°.
证明:如图2中,延长FD到M使得DF=DM,连接BM,EM.
在△DFC和△DMB中,
∴△DFC≌△DMB,
∴∠C=∠MBD=60°,BM=CF,
∵DE=DF=DM,∠EDM=180°-∠EDF=60°,
∴△EDM是等边三角形,
∴EM=DE,
∴EB、ED、CF能围成△EBM,
最大内角∠EBM=∠EBC+∠DBM=60°+60°=120°.
同课章节目录
