14.1.1 直角三角形三边的关系课件(25张PPT)
文档属性
| 名称 | 14.1.1 直角三角形三边的关系课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 16:16:47 | ||
图片预览





文档简介
(共25张PPT)
14.1.1 直角三角形三边的关系
华师大版 八年级上册
教学目标
1.体验勾股定理的探索.
2.会用勾股定理求直角三角形的边长.
【教学重点】用勾股定理求直角三角形的边长.
【教学难点】用拼图法证明勾股定理.
新知导入
你知道2002年在北京召开的国际数学家大会(ICM-2002)吗?在这次大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案,它就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.
新知讲解
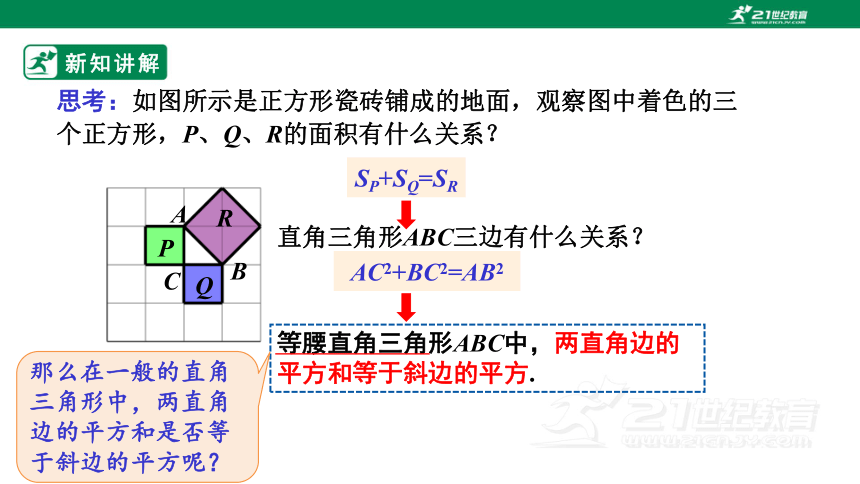
思考:如图所示是正方形瓷砖铺成的地面,观察图中着色的三个正方形,P、Q、R的面积有什么关系?
P
Q
R
A
C
B
SP+SQ=SR
直角三角形ABC三边有什么关系?
AC2+BC2=AB2
等腰直角三角形ABC中,两直角边的平方和等于斜边的平方.
那么在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?
新知讲解
试
一
试
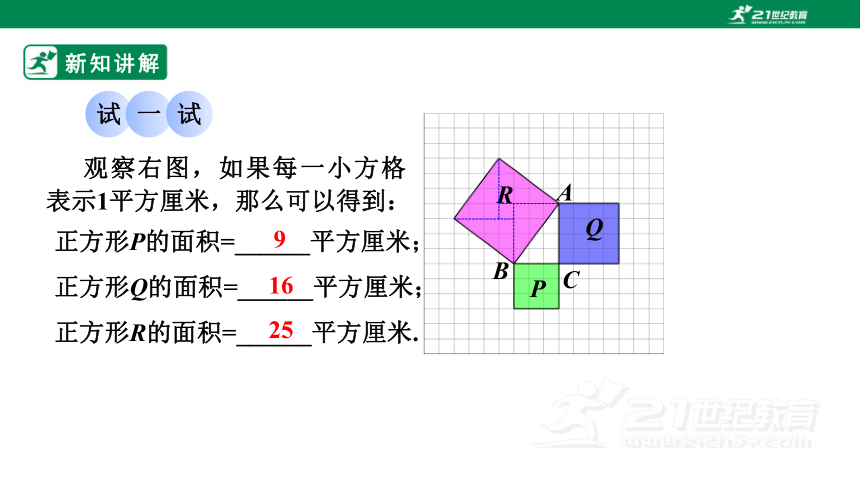
观察右图,如果每一小方格表示1平方厘米,那么可以得到:
P
Q
R
A
B
C
正方形P的面积=______平方厘米;
正方形Q的面积=______平方厘米;
正方形R的面积=______平方厘米.
9
16
25
新知讲解
P
Q
R
A
B
C
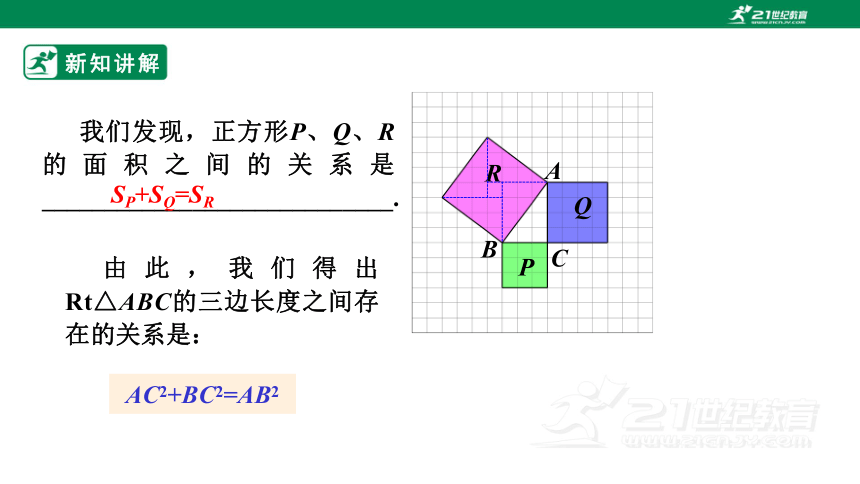
我们发现,正方形P、Q、R的面积之间的关系是____________________________.
SP+SQ=SR
由此,我们得出Rt△ABC的三边长度之间存在的关系是:
AC2+BC2=AB2
新知讲解
做
一
做
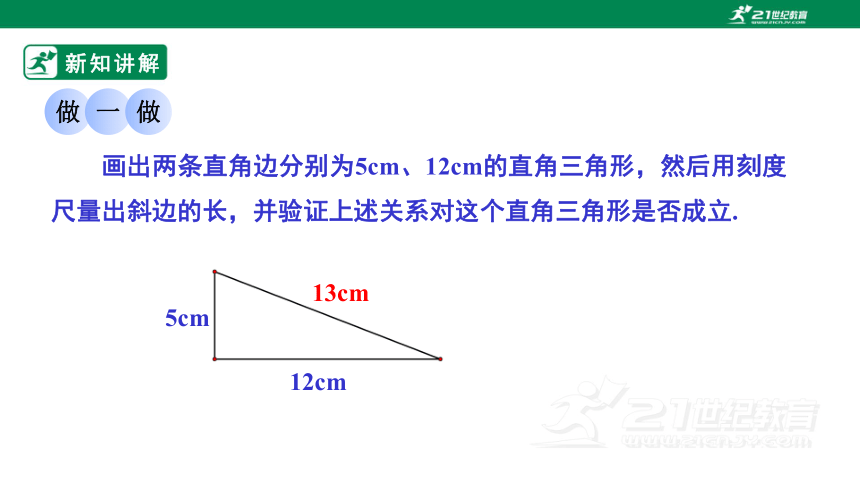
画出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立.
5cm
12cm
13cm
新知讲解
概括
由上面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有
a2+b2=c2,
a
b
c
这种关系我们称为勾股定理.
即 直角三角形两直角边的平方和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
新知讲解
读
一
读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,它标志着中国古代的数学成就.
勾
股
a
b
c
股
勾
弦
新知讲解
思考:怎样证明勾股定理?
左图是弦图的示意图,它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.
大正方形的面积=c2.
四个全等的直角三角形和小正方形的面积之和= .
即a2+b2=c2.
新知讲解
做
一
做
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,也能证明勾股定理.请你试一试,写出完整的证明过程.
新知讲解
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积之和= .
由题可知(a+b)2=2ab+c2,
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
例题讲解
例1 在Rt△ABC中,已知∠B=90°,AB=6, BC=8.求AC.
解:根据勾股定理,可得
AB2+ BC2= AC2.
所以
应用勾股定理,由直角
三角形任意两边的长度,可以求出第三边的长度.
巩固练习
(1)在Rt△ABC中,∠C=90°,AC=5,BC=12,则AB=________;
(2)在Rt△ABC中,∠C=90°,AB=25,AC=20,则BC=________;
(3)在Rt△ABC中,∠C=90°,它的两边是6和8,则它的第三边长是________.
13
15
10或
例题讲解
例2 如图, Rt△ABC的斜边AC比直角边
AB长2cm,另一直角边BC长为6 cm.求AC的长.
解 由已知AB=AC-2,BC=6cm,
根据勾股定理 ,可得
AB2+BC2=(AC-2)2+62=AC2,
解得 AC = 10( cm).
C
A
B
例题讲解
例3 如图,为了求出位于湖两岸的点A、B之间的距离,一名观测者在点C设桩,使△ABC恰好为直角三角形.通过测量,得到AC的长为160米,BC的长为128米.问从点A穿过湖到点B有多远
例题讲解
解 如图,在Rt△ABC中,
AC=160米,BC=128米,
根据勾股定理,可得
=96(米).
答:从点A穿过湖到点B有96米.
课堂总结
勾股定理
定理
验证
1.求边长、面积,证明线段之间的平方关系
2.勾股定理的实际应用
应用
直角三角形两直角边的平方和等于斜边的平方
用拼图法验证勾股定理
课堂练习
教材111页练习2
1.在Rt△ABC中,AB=c,BC=a,AC=b,∠C=90°.
(1)已知a=6,c=10,求b; (2)已知a=24,c=25,求b.
解:(1)在Rt△ABC中,∠C=90°,a=6,c=10,由勾股定理,得 .
(2)在Rt△ABC中,∠C=90°,a=24,c=25,根据勾股定理,得 .
课堂练习
教材111页练习2
2.如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?(精确到0.1厘米)
解:分两种情况.①若这两边是直角边,则斜边长是
=5,周长是3+4+5=12(厘米);②若这两边中较长的边是斜边,则斜边长为4厘米,所以另一直角边的长为
(厘米),周长是 (厘米),所以此三角形的周长是12厘米或9.6厘米.
课堂练习
教材112页练习1
3.如图,小方格都是边长为1的正方形.求四边形ABCD的面积与周长. (精确到0.1)
解:S大正方形=5×5=25,
四个直角三角形的面积之和=1×2×
+2×4× +3×3× +2×3× =12.5
所以S四边形ABCD=25-12.5=12.5.
课堂练习
教材112页练习2
3.如图,小方格都是边长为1的正方形.求四边形ABCD的面积与周长. (精确到0.1)
C四边形ABCD=AD+DC+BC+AB
答:四边形ABCD的面积是12.5,周长约是14.6.
课堂练习
教材112页练习2
4.假期中,王强和同学到某海岛上去探宝旅游.按照探宝图(如图),他们在点A处登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到了宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?
C
解:如图所示,过点B作AD的垂线,垂足为C,
则△ABC为直角三角形,且AC=8-3+1=6,BC=6+2=8,
所以AB= =10(千米).
答:登陆点A到宝藏埋藏点B的直线距离是10千米.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.1.1 直角三角形三边的关系
华师大版 八年级上册
教学目标
1.体验勾股定理的探索.
2.会用勾股定理求直角三角形的边长.
【教学重点】用勾股定理求直角三角形的边长.
【教学难点】用拼图法证明勾股定理.
新知导入
你知道2002年在北京召开的国际数学家大会(ICM-2002)吗?在这次大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案,它就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.
新知讲解
思考:如图所示是正方形瓷砖铺成的地面,观察图中着色的三个正方形,P、Q、R的面积有什么关系?
P
Q
R
A
C
B
SP+SQ=SR
直角三角形ABC三边有什么关系?
AC2+BC2=AB2
等腰直角三角形ABC中,两直角边的平方和等于斜边的平方.
那么在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?
新知讲解
试
一
试
观察右图,如果每一小方格表示1平方厘米,那么可以得到:
P
Q
R
A
B
C
正方形P的面积=______平方厘米;
正方形Q的面积=______平方厘米;
正方形R的面积=______平方厘米.
9
16
25
新知讲解
P
Q
R
A
B
C
我们发现,正方形P、Q、R的面积之间的关系是____________________________.
SP+SQ=SR
由此,我们得出Rt△ABC的三边长度之间存在的关系是:
AC2+BC2=AB2
新知讲解
做
一
做
画出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立.
5cm
12cm
13cm
新知讲解
概括
由上面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有
a2+b2=c2,
a
b
c
这种关系我们称为勾股定理.
即 直角三角形两直角边的平方和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
新知讲解
读
一
读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,它标志着中国古代的数学成就.
勾
股
a
b
c
股
勾
弦
新知讲解
思考:怎样证明勾股定理?
左图是弦图的示意图,它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.
大正方形的面积=c2.
四个全等的直角三角形和小正方形的面积之和= .
即a2+b2=c2.
新知讲解
做
一
做
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,也能证明勾股定理.请你试一试,写出完整的证明过程.
新知讲解
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积之和= .
由题可知(a+b)2=2ab+c2,
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
例题讲解
例1 在Rt△ABC中,已知∠B=90°,AB=6, BC=8.求AC.
解:根据勾股定理,可得
AB2+ BC2= AC2.
所以
应用勾股定理,由直角
三角形任意两边的长度,可以求出第三边的长度.
巩固练习
(1)在Rt△ABC中,∠C=90°,AC=5,BC=12,则AB=________;
(2)在Rt△ABC中,∠C=90°,AB=25,AC=20,则BC=________;
(3)在Rt△ABC中,∠C=90°,它的两边是6和8,则它的第三边长是________.
13
15
10或
例题讲解
例2 如图, Rt△ABC的斜边AC比直角边
AB长2cm,另一直角边BC长为6 cm.求AC的长.
解 由已知AB=AC-2,BC=6cm,
根据勾股定理 ,可得
AB2+BC2=(AC-2)2+62=AC2,
解得 AC = 10( cm).
C
A
B
例题讲解
例3 如图,为了求出位于湖两岸的点A、B之间的距离,一名观测者在点C设桩,使△ABC恰好为直角三角形.通过测量,得到AC的长为160米,BC的长为128米.问从点A穿过湖到点B有多远
例题讲解
解 如图,在Rt△ABC中,
AC=160米,BC=128米,
根据勾股定理,可得
=96(米).
答:从点A穿过湖到点B有96米.
课堂总结
勾股定理
定理
验证
1.求边长、面积,证明线段之间的平方关系
2.勾股定理的实际应用
应用
直角三角形两直角边的平方和等于斜边的平方
用拼图法验证勾股定理
课堂练习
教材111页练习2
1.在Rt△ABC中,AB=c,BC=a,AC=b,∠C=90°.
(1)已知a=6,c=10,求b; (2)已知a=24,c=25,求b.
解:(1)在Rt△ABC中,∠C=90°,a=6,c=10,由勾股定理,得 .
(2)在Rt△ABC中,∠C=90°,a=24,c=25,根据勾股定理,得 .
课堂练习
教材111页练习2
2.如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?(精确到0.1厘米)
解:分两种情况.①若这两边是直角边,则斜边长是
=5,周长是3+4+5=12(厘米);②若这两边中较长的边是斜边,则斜边长为4厘米,所以另一直角边的长为
(厘米),周长是 (厘米),所以此三角形的周长是12厘米或9.6厘米.
课堂练习
教材112页练习1
3.如图,小方格都是边长为1的正方形.求四边形ABCD的面积与周长. (精确到0.1)
解:S大正方形=5×5=25,
四个直角三角形的面积之和=1×2×
+2×4× +3×3× +2×3× =12.5
所以S四边形ABCD=25-12.5=12.5.
课堂练习
教材112页练习2
3.如图,小方格都是边长为1的正方形.求四边形ABCD的面积与周长. (精确到0.1)
C四边形ABCD=AD+DC+BC+AB
答:四边形ABCD的面积是12.5,周长约是14.6.
课堂练习
教材112页练习2
4.假期中,王强和同学到某海岛上去探宝旅游.按照探宝图(如图),他们在点A处登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到了宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?
C
解:如图所示,过点B作AD的垂线,垂足为C,
则△ABC为直角三角形,且AC=8-3+1=6,BC=6+2=8,
所以AB= =10(千米).
答:登陆点A到宝藏埋藏点B的直线距离是10千米.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
