14.2.1 勾股定理的应用课件(19张PPT)
文档属性
| 名称 | 14.2.1 勾股定理的应用课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-04 16:22:35 | ||
图片预览




文档简介
(共19张PPT)
14.2.1 勾股定理的应用
华师大版 八年级上册
教学目标
1.会用勾股定理解决较综合的问题.
2.树立数形结合的思想.
【教学重点】勾股定理的综合应用.
【教学难点】勾股定理的综合应用.
复习导入
c
a
b
在△ABC中,∠C=90°.
(1)若b=8,c=10,则a= ;
(2)若a=5,b=10,则c = ;
(3)若a=2,∠A=30° ,则 b = ;
C
A
B
6
11.2
3.5
(2)、(3)两题结果精确到0.1
新知讲解
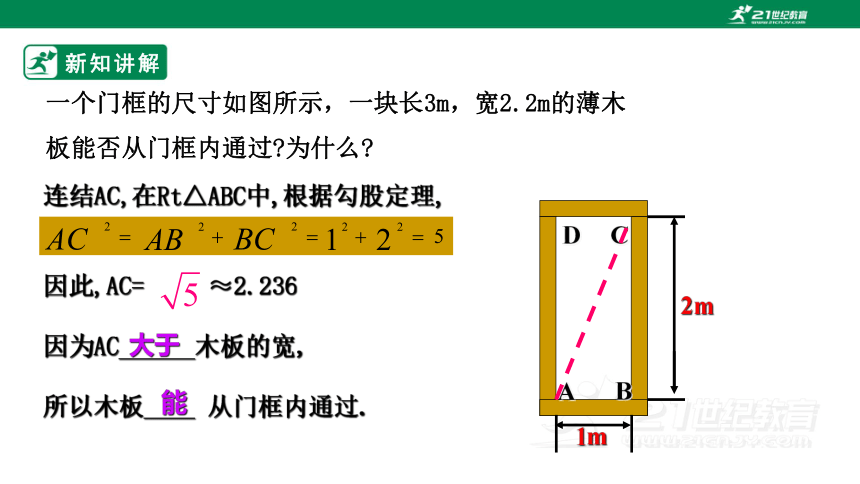
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么
2m
D
C
A
B
连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.
大于
能
1m
例题讲解
例1
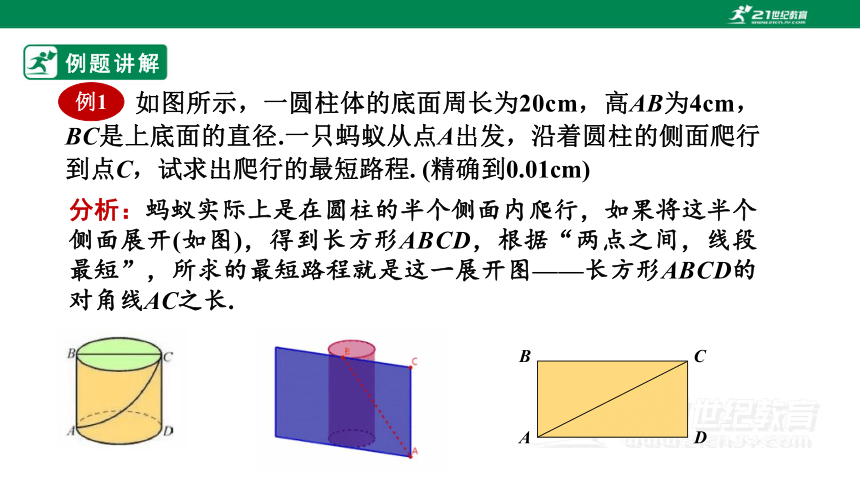
如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
分析:蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开(如图),得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
A
B
C
D
例题讲解
解:如图所示,在Rt△ABC中,BC=底面周长的一半=10cm.由勾股定理,可得
A
B
C
D
答:爬行的最短路程约为10. 77 cm.
巩固练习
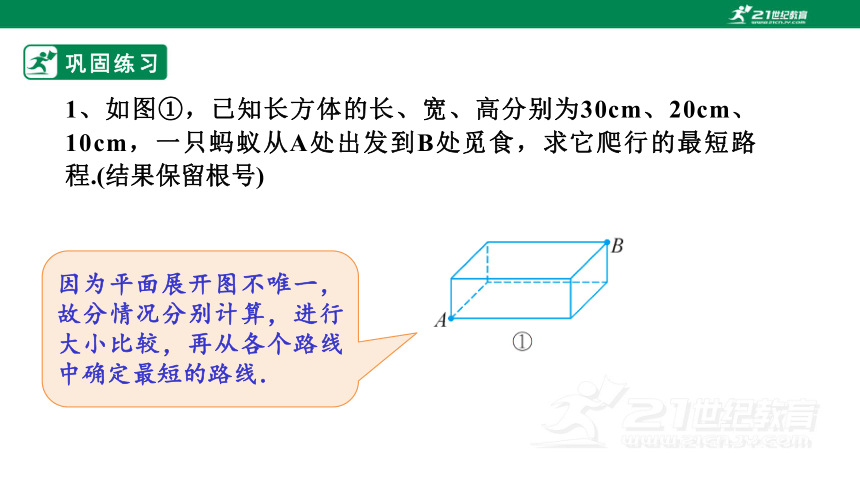
1、如图①,已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它爬行的最短路程.(结果保留根号)
因为平面展开图不唯一,故分情况分别计算,进行大小比较,再从各个路线中确定最短的路线.
新知讲解
解:长方体的展开图如图
如图②,展开前面、右面,由勾股定理得AB=
=
如图③,展开前面、上面,由勾股定理得AB=
=
如图④,展开左面、上面,由勾股定理得AB=
=
∵ ,∴爬行最短路程为 cm.
新知讲解
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上.如左图所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的.若将树干的侧面展开成一个平面,如右图所示,可清楚的看出葛藤在这个平面上是沿直线上升的.
例题讲解
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门(厂门上方为半圆形拱门)
分析:由于车宽1.6米,所以卡车能否通过,只要比较距厂门中线0.8米处的高度与车高即可.如图所示,点D在离厂门中线0.8米处,且CD⊥AB,与地面相交于点H.
例2
例题讲解
解:在Rt△OCD中,由勾股定理,可得
CH=CD+DH=0.6+2.3=2.9>2.5.
可见高度上有0.4米的余量,因此卡车能通过厂门.
巩固练习
2、有一根高为16米的电线杆在A处断裂,如图所示,电线杆的顶部C落在离电线杆底部B处8米远的地方,求电线杆断裂处A到地面的距离.
根据题意可知在Rt△ABC中,∠ABC =90°,BC=8米,AB+AC=16米.若设AB=x米,则AC=(16-x)米,然后根据勾股定理列出方程求解.
巩固练习
解:在Rt△ABC中,∠ABC=90°.
设AB=x米,则AC=(16-x)米.
根据勾股定理,得x2+82=(16-x)2,
解得x=6,即AB=6米.
答:电线杆断裂处A到地面的距离为6米.
课堂总结
1.要记住勾股定理及逆定理的内容.
2.把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决最短路程问题.
随堂练习
1.为了加固电线杆,往往需要给它拉上一条固定于地面的钢缆如图,从电线杆离地面5米处向地面拉一条7米长的钢缆,求钢缆在地面上的固定点A到电线杆底部B的距离. (精确到0.1米)
解:由勾股定理可知AB= (米).
答:钢缆在地面上的固定点A到电线杆底部B的距离约为4.9米.
随堂练习
2.轮船A以16海里/时的速度离开港口O向东北方向航行,轮船B在同时同地以12海里/时的速度向西北方向航行.试求A、B两船离开港口O一个半小时后的距离.
解: (海里).
随堂练习
在证明的等式中含有线段的平方关系时,一般考虑构造直角三角形,运用等式的性质进行变形.
3.如图所示,在 ABC中,AB=AC,点D在CB延长线上,试说明:AD -AB =BD·CD
∟
A
B
C
D
E
在Rt ADE和Rt AEC中,
根据勾股定理得,
AD =AE +DE , AC =AE +EC
∵AB=AC AE⊥BC
∴EB=EC
∴AD -AB =DE -EC
=(DE-EC)·(DE+EC)
=(DE-EB)·DC
=BD·DC
即AD -AB =BD·CD
解: 作高AE
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.2.1 勾股定理的应用
华师大版 八年级上册
教学目标
1.会用勾股定理解决较综合的问题.
2.树立数形结合的思想.
【教学重点】勾股定理的综合应用.
【教学难点】勾股定理的综合应用.
复习导入
c
a
b
在△ABC中,∠C=90°.
(1)若b=8,c=10,则a= ;
(2)若a=5,b=10,则c = ;
(3)若a=2,∠A=30° ,则 b = ;
C
A
B
6
11.2
3.5
(2)、(3)两题结果精确到0.1
新知讲解
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么
2m
D
C
A
B
连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.
大于
能
1m
例题讲解
例1
如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
分析:蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开(如图),得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
A
B
C
D
例题讲解
解:如图所示,在Rt△ABC中,BC=底面周长的一半=10cm.由勾股定理,可得
A
B
C
D
答:爬行的最短路程约为10. 77 cm.
巩固练习
1、如图①,已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它爬行的最短路程.(结果保留根号)
因为平面展开图不唯一,故分情况分别计算,进行大小比较,再从各个路线中确定最短的路线.
新知讲解
解:长方体的展开图如图
如图②,展开前面、右面,由勾股定理得AB=
=
如图③,展开前面、上面,由勾股定理得AB=
=
如图④,展开左面、上面,由勾股定理得AB=
=
∵ ,∴爬行最短路程为 cm.
新知讲解
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上.如左图所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的.若将树干的侧面展开成一个平面,如右图所示,可清楚的看出葛藤在这个平面上是沿直线上升的.
例题讲解
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门(厂门上方为半圆形拱门)
分析:由于车宽1.6米,所以卡车能否通过,只要比较距厂门中线0.8米处的高度与车高即可.如图所示,点D在离厂门中线0.8米处,且CD⊥AB,与地面相交于点H.
例2
例题讲解
解:在Rt△OCD中,由勾股定理,可得
CH=CD+DH=0.6+2.3=2.9>2.5.
可见高度上有0.4米的余量,因此卡车能通过厂门.
巩固练习
2、有一根高为16米的电线杆在A处断裂,如图所示,电线杆的顶部C落在离电线杆底部B处8米远的地方,求电线杆断裂处A到地面的距离.
根据题意可知在Rt△ABC中,∠ABC =90°,BC=8米,AB+AC=16米.若设AB=x米,则AC=(16-x)米,然后根据勾股定理列出方程求解.
巩固练习
解:在Rt△ABC中,∠ABC=90°.
设AB=x米,则AC=(16-x)米.
根据勾股定理,得x2+82=(16-x)2,
解得x=6,即AB=6米.
答:电线杆断裂处A到地面的距离为6米.
课堂总结
1.要记住勾股定理及逆定理的内容.
2.把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决最短路程问题.
随堂练习
1.为了加固电线杆,往往需要给它拉上一条固定于地面的钢缆如图,从电线杆离地面5米处向地面拉一条7米长的钢缆,求钢缆在地面上的固定点A到电线杆底部B的距离. (精确到0.1米)
解:由勾股定理可知AB= (米).
答:钢缆在地面上的固定点A到电线杆底部B的距离约为4.9米.
随堂练习
2.轮船A以16海里/时的速度离开港口O向东北方向航行,轮船B在同时同地以12海里/时的速度向西北方向航行.试求A、B两船离开港口O一个半小时后的距离.
解: (海里).
随堂练习
在证明的等式中含有线段的平方关系时,一般考虑构造直角三角形,运用等式的性质进行变形.
3.如图所示,在 ABC中,AB=AC,点D在CB延长线上,试说明:AD -AB =BD·CD
∟
A
B
C
D
E
在Rt ADE和Rt AEC中,
根据勾股定理得,
AD =AE +DE , AC =AE +EC
∵AB=AC AE⊥BC
∴EB=EC
∴AD -AB =DE -EC
=(DE-EC)·(DE+EC)
=(DE-EB)·DC
=BD·DC
即AD -AB =BD·CD
解: 作高AE
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
