人教版八年级下册17.2勾股定理的逆定理课件(共18张PPT)
文档属性
| 名称 | 人教版八年级下册17.2勾股定理的逆定理课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 20:16:14 | ||
图片预览






文档简介
(共18张PPT)
数学课堂基本规范
预备铃响进教室,全体做到静快齐
学习用品准备好,心宁神定坐姿正
细心听讲不插话,眼到耳到心更到
自主学习并不难,学辅资料好帮手
勤做笔记勤思考,圈点勾画有取舍
独立作业勤动脑,不要抄袭不拖延
学习过程
复习回顾
自主学习
合作探究
快乐晋级
课堂小结
学习目标
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
1
大家来说说
勇攀高峰
1.直角三角形有哪些性质
2.如何判断三角形是
直角三角形
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
新课导入
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
1
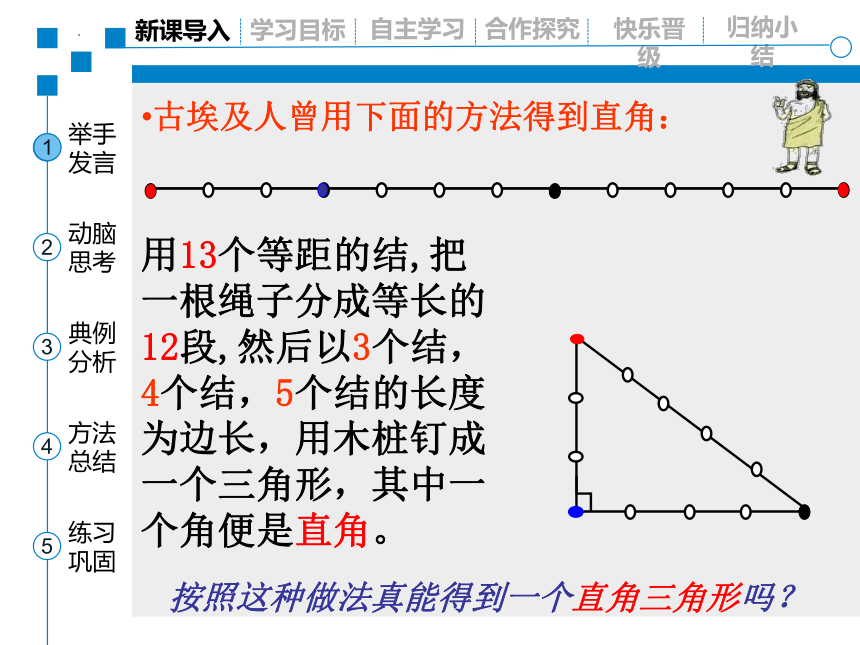
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
人教版八年级(下)册第十七章《勾股定理的逆定理》的第一课时
勾股定理的逆定理
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
X
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
学习目标
1、了解互逆命题和互逆定理的概念。
学习重难点
2、理解勾股定理的逆定理的证明方法。
3、掌握勾股定理的逆定理,并能利用勾股定理的逆定理
判定一个三角形是否为直角三角形。
重点:勾股定理的逆定理及应用;
难点:勾股定理逆定理的证明。
4、会认识并判别勾股数。
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
2
问题1:请同学们观察,这个三角形
的三条边有什么关系吗
3
4
5
问题2:下面的三组数分别是一个三角形的三边长a,b,c
2.5,6,6.5; 6,8,10。
(1)这三组数都满足
吗?
(2)画出图形,它们都是直角三角形吗?
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
2
问题3:探索思考:
由上面几个例子你发现了什么吗
能以命题的形式说出你的观点吗!
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
勾股定理的逆命题
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
2
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
勾股定理的逆命题
如果直角三角形两直角边分别为
a,b,斜边为c,那么有
a2 + b2 = c2
勾股定理
互逆命题
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
4
问题4:能否证明这个定理呢?
3
4
5
A
C
B
古埃及人的做法:
△ABC中, BC=3、 AC=4、AB=5.
这两个三角形有什么关系?
我们作Rt△A'B'C',使B'C'=3,A'C'=4.
3
4
A'
C'
B'
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
3
应用验证
判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是
直角三角形,只要看两条较小边的平方和是否等
于最大边的平方。
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
5
我国是最早了解勾股定理的国家之一。早在4 0 0 0多年以前,我国人民就应用了这条定理。我国最早的一部数学及天文著作《周髀算经》记载了这个定理,该书称直立着的标竿为“股”,地面上的日影为“勾”,斜边为“弦”。于是这个定理可记为:勾2+股2=弦2。这就是勾股定理的来历。
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
5
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(3) a:b: c=3:4:5 _____ _____ ;
是
是
不是
∠ A=900
∠ C=900
像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
3
能力提升
相信自己是最棒的!
“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
E
Q
R
N
远航
海天
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
5
在△ABC中,a=15, b=17, c=8,求此三角形的面积。
∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为
8
15
17
A
B
C
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
1
2
3
4
5
请谈谈你的收获
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
作业:
教科书P28 2,3,
THE END
Thank you
数学课堂基本规范
预备铃响进教室,全体做到静快齐
学习用品准备好,心宁神定坐姿正
细心听讲不插话,眼到耳到心更到
自主学习并不难,学辅资料好帮手
勤做笔记勤思考,圈点勾画有取舍
独立作业勤动脑,不要抄袭不拖延
学习过程
复习回顾
自主学习
合作探究
快乐晋级
课堂小结
学习目标
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
1
大家来说说
勇攀高峰
1.直角三角形有哪些性质
2.如何判断三角形是
直角三角形
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
新课导入
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
1
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
人教版八年级(下)册第十七章《勾股定理的逆定理》的第一课时
勾股定理的逆定理
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
X
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
学习目标
1、了解互逆命题和互逆定理的概念。
学习重难点
2、理解勾股定理的逆定理的证明方法。
3、掌握勾股定理的逆定理,并能利用勾股定理的逆定理
判定一个三角形是否为直角三角形。
重点:勾股定理的逆定理及应用;
难点:勾股定理逆定理的证明。
4、会认识并判别勾股数。
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
2
问题1:请同学们观察,这个三角形
的三条边有什么关系吗
3
4
5
问题2:下面的三组数分别是一个三角形的三边长a,b,c
2.5,6,6.5; 6,8,10。
(1)这三组数都满足
吗?
(2)画出图形,它们都是直角三角形吗?
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
2
问题3:探索思考:
由上面几个例子你发现了什么吗
能以命题的形式说出你的观点吗!
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
勾股定理的逆命题
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
2
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
勾股定理的逆命题
如果直角三角形两直角边分别为
a,b,斜边为c,那么有
a2 + b2 = c2
勾股定理
互逆命题
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
4
问题4:能否证明这个定理呢?
3
4
5
A
C
B
古埃及人的做法:
△ABC中, BC=3、 AC=4、AB=5.
这两个三角形有什么关系?
我们作Rt△A'B'C',使B'C'=3,A'C'=4.
3
4
A'
C'
B'
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
3
应用验证
判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是
直角三角形,只要看两条较小边的平方和是否等
于最大边的平方。
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
5
我国是最早了解勾股定理的国家之一。早在4 0 0 0多年以前,我国人民就应用了这条定理。我国最早的一部数学及天文著作《周髀算经》记载了这个定理,该书称直立着的标竿为“股”,地面上的日影为“勾”,斜边为“弦”。于是这个定理可记为:勾2+股2=弦2。这就是勾股定理的来历。
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
5
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(3) a:b: c=3:4:5 _____ _____ ;
是
是
不是
∠ A=900
∠ C=900
像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
3
能力提升
相信自己是最棒的!
“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
E
Q
R
N
远航
海天
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
5
在△ABC中,a=15, b=17, c=8,求此三角形的面积。
∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为
8
15
17
A
B
C
归纳小结
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
复习回顾
学习目标
自主学习
合作探究
快乐晋级
1
2
3
5
4
举手发言
动脑思考
典例分析
方法总结
练习巩固
1
2
3
4
5
请谈谈你的收获
单击此处编辑母版标题样式
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
作业:
教科书P28 2,3,
THE END
Thank you
