沪科版九年级上册21.5反比例函数(第1课时)课件(共16张PPT)
文档属性
| 名称 | 沪科版九年级上册21.5反比例函数(第1课时)课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
21.5 反比例函数
一、情境引入
动手操作:
画一个面积为12cm2的矩形
新课导入
长×宽 = 12 cm2
12 cm2
像这种两个变量的乘积一定,它们的关系叫做反比例关系.
,所画矩形的长和宽有什么关系?
反比例
举例:
路程(一定)=速度×时间
总价(一定) =单价×数量
工作总量(一定) =工作时间×工作效率
反比例
反比例
反比例
一、情境引入
问题1 某村有耕地200 hm2,人口数量x逐年发生变化,该村人均耕地面积y hm2与人口数量x之间有怎样的函数关系
全村耕地面积应是人均耕地面积与人口数量的乘积,即yx =200
,所以变量y hm2与x之间的函数关系可以表示为:
新课讲授
一、情境引入
问题2 某市距省城248 km,汽车行驶全程所需的时间t h与平均速度v km/h之间有怎样的函数关系?
由路程s =vt,
变量t h与v km/h之间的函数关系可以表示为
一、情境引入
问题3 某住宅小区要种植一块面积为 1 000 m2 的矩形草坪,草坪的长 a m与宽 b m之间有怎样的函数关系?
由面积s =ab,
变量a m与b m之间的函数关系可以表示为
一、情境引入
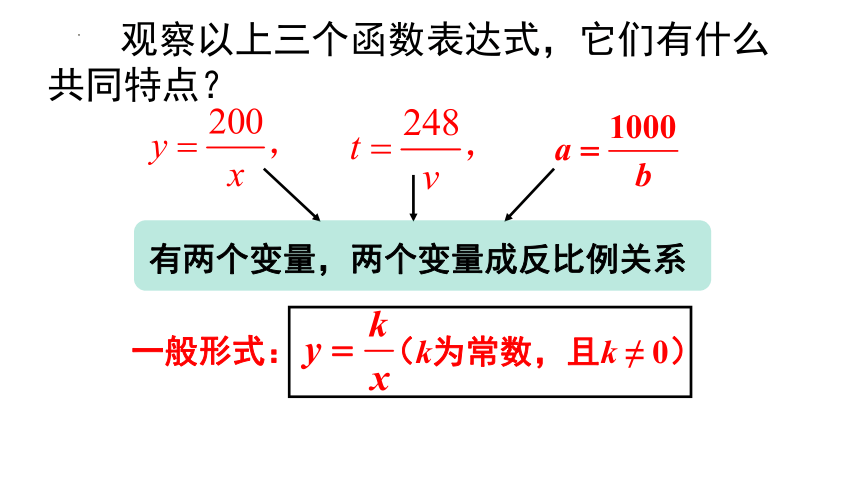
观察以上三个函数表达式,它们有什么共同特点?
(k为常数,且k ≠ 0)
有两个变量,两个变量成反比例关系
一般形式:
一、情境引入
自变量 x 的取值范围是不等于 0 的一切实数.
一般地,表达式形如 (k 为常数,且k ≠ 0)的函数,叫做反比例函数.
一、情境引入
思考:反比例函数除了可以用 (k ≠ 0) 的形式表示,还有没有其他表示形式?
(k ≠ 0)
1.下列y是不是x反比例函数?若是,请指出k的值.
是,k = 4
不是
不是
是,
新知巩固
是,k =5
2. 已知函数 是反比例函数,则 k 必须满足 .
3. 当m= 时, 是反比例函数.
k≠3
±1
例1 在压力不变的情况下,某物体承受的压强 p Pa是它的受力面积S m2的反比例函数,如图.
(1)求 p和S之间的函数表达式;
(2)当S=0.5时,求物体承受的
压强 p 的值.
经典例题
①设出反比例函数表达式;
②将自变量与函数值代入表达式,得到方程;
③解方程,求出待定系数;
④写出反比例函数表达式.
用待定系数法求反比例函数表达式的一般步骤:
一定质量的氧气,它的密度ρ与它的体积V成反比例关系,当 V =10 m3 时,ρ =1.43 kg / m3.
(1)求 ρ 与 V 之间的函数表达式;
(2)当 V =2 m3 时,求氧气的密度 ρ的值.
练一练
反比例函数
①设;②代;③解;④写
一般地,形如 (k 为常数,k ≠ 0)的函数,叫做反比例函数.
概念
求表达式
今天你有什么收获?
课堂小结
表示形式
必做题:课本第44页练习1题,48页1~3题.
选做题:已知 y 与 x+1 成反比例,
并且当 x = 3 时,y = 4.
(1) 写出 y 关于 x 的函数解析式;
(2) 当 x = 7 时,求 y 的值.
作业布置
21.5 反比例函数
一、情境引入
动手操作:
画一个面积为12cm2的矩形
新课导入
长×宽 = 12 cm2
12 cm2
像这种两个变量的乘积一定,它们的关系叫做反比例关系.
,所画矩形的长和宽有什么关系?
反比例
举例:
路程(一定)=速度×时间
总价(一定) =单价×数量
工作总量(一定) =工作时间×工作效率
反比例
反比例
反比例
一、情境引入
问题1 某村有耕地200 hm2,人口数量x逐年发生变化,该村人均耕地面积y hm2与人口数量x之间有怎样的函数关系
全村耕地面积应是人均耕地面积与人口数量的乘积,即yx =200
,所以变量y hm2与x之间的函数关系可以表示为:
新课讲授
一、情境引入
问题2 某市距省城248 km,汽车行驶全程所需的时间t h与平均速度v km/h之间有怎样的函数关系?
由路程s =vt,
变量t h与v km/h之间的函数关系可以表示为
一、情境引入
问题3 某住宅小区要种植一块面积为 1 000 m2 的矩形草坪,草坪的长 a m与宽 b m之间有怎样的函数关系?
由面积s =ab,
变量a m与b m之间的函数关系可以表示为
一、情境引入
观察以上三个函数表达式,它们有什么共同特点?
(k为常数,且k ≠ 0)
有两个变量,两个变量成反比例关系
一般形式:
一、情境引入
自变量 x 的取值范围是不等于 0 的一切实数.
一般地,表达式形如 (k 为常数,且k ≠ 0)的函数,叫做反比例函数.
一、情境引入
思考:反比例函数除了可以用 (k ≠ 0) 的形式表示,还有没有其他表示形式?
(k ≠ 0)
1.下列y是不是x反比例函数?若是,请指出k的值.
是,k = 4
不是
不是
是,
新知巩固
是,k =5
2. 已知函数 是反比例函数,则 k 必须满足 .
3. 当m= 时, 是反比例函数.
k≠3
±1
例1 在压力不变的情况下,某物体承受的压强 p Pa是它的受力面积S m2的反比例函数,如图.
(1)求 p和S之间的函数表达式;
(2)当S=0.5时,求物体承受的
压强 p 的值.
经典例题
①设出反比例函数表达式;
②将自变量与函数值代入表达式,得到方程;
③解方程,求出待定系数;
④写出反比例函数表达式.
用待定系数法求反比例函数表达式的一般步骤:
一定质量的氧气,它的密度ρ与它的体积V成反比例关系,当 V =10 m3 时,ρ =1.43 kg / m3.
(1)求 ρ 与 V 之间的函数表达式;
(2)当 V =2 m3 时,求氧气的密度 ρ的值.
练一练
反比例函数
①设;②代;③解;④写
一般地,形如 (k 为常数,k ≠ 0)的函数,叫做反比例函数.
概念
求表达式
今天你有什么收获?
课堂小结
表示形式
必做题:课本第44页练习1题,48页1~3题.
选做题:已知 y 与 x+1 成反比例,
并且当 x = 3 时,y = 4.
(1) 写出 y 关于 x 的函数解析式;
(2) 当 x = 7 时,求 y 的值.
作业布置
