2022-2023学年苏科版数学八年级上册2.4线段、角的轴对称性复习课件(共25张PPT)
文档属性
| 名称 | 2022-2023学年苏科版数学八年级上册2.4线段、角的轴对称性复习课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
线段、角的轴对称性
线段的轴对称性
1
1.线段的轴对称性
知识点复习:
线段的对称轴
线段垂直平分线的判定
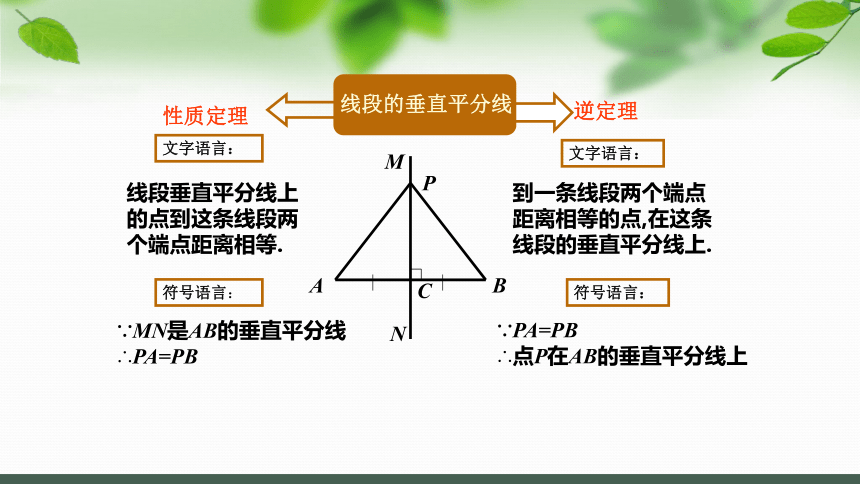
线段是轴对称图形,线段的垂直平分线是它的对称轴.
到线段两端距离相等的点,在这条线段的垂直平分线上.
线段的垂直平分线上的点到线段两端的距离相等.
线段垂直平分线的性质
逆定理
性质定理
文字语言:
文字语言:
线段垂直平分线上
的点到这条线段两
个端点距离相等.
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
C
B
P
M
N
符号语言:
符号语言:
∵MN是AB的垂直平分线∴PA=PB
∵PA=PB
∴点P在AB的垂直平分线上
线段的垂直平分线
热身练习
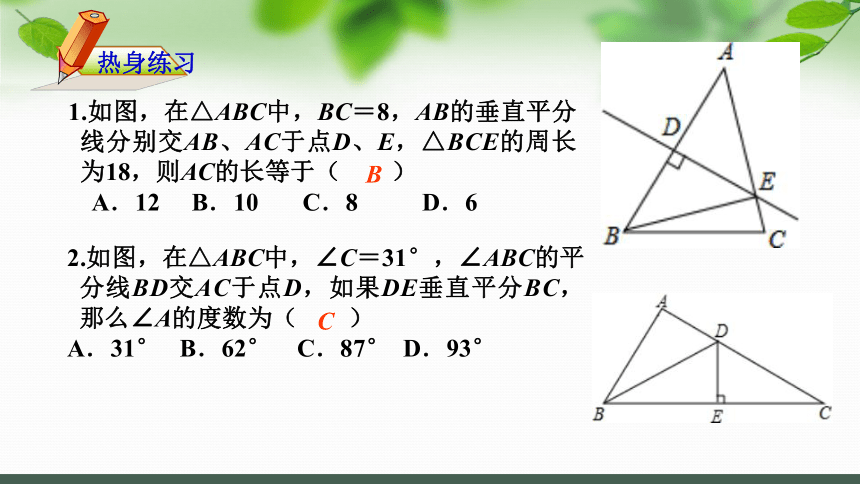
1.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长等于( )
A.12 B.10 C.8 D.6
B
2.如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A的度数为( )
A.31° B.62° C.87° D.93°
C
角的轴对称性
2
2.角的轴对称性
角的对称轴
角平分线的判定
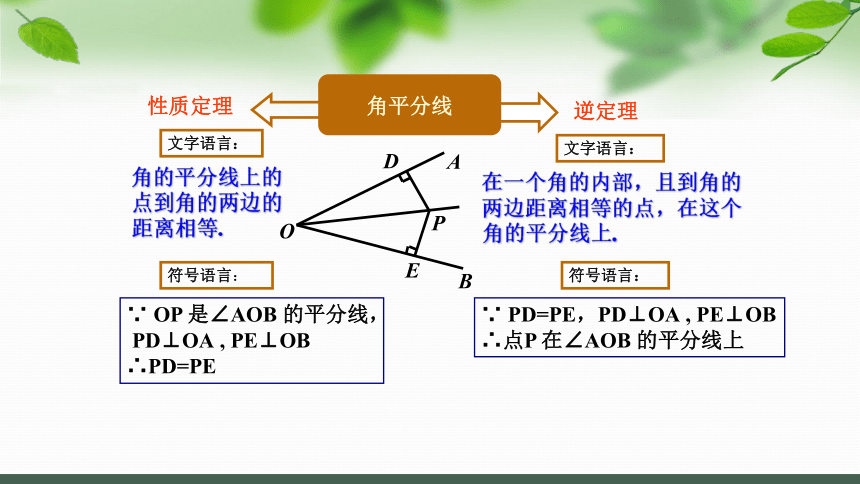
角是轴对称图形,角平分线所在直线是它的对称轴.
知识点复习:
角平分线上的点到角的两边距离相等.
角平分线的性质
到角的两边距离相等的点,在这个角的平分线上.
注意: 不能写角平分线因为对称轴指的是直线
逆定理
性质定理
文字语言:
文字语言:
角的平分线上的
点到角的两边的
距离相等.
符号语言:
符号语言:
B
A
D
O
P
E
在一个角的内部,且到角的
两边距离相等的点,在这个
角的平分线上.
∵ PD=PE,PD⊥OA , PE⊥OB
∴点P 在∠AOB 的平分线上
角平分线
∵ OP 是∠AOB 的平分线,
PD⊥OA , PE⊥OB
∴PD=PE
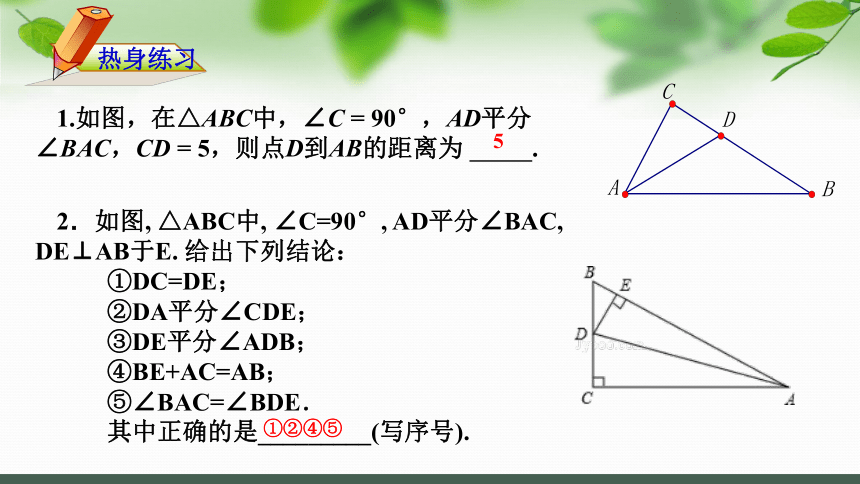
1.如图,在△ABC中,∠C = 90°,AD平分∠BAC,CD = 5,则点D到AB的距离为 .
5
2.如图, △ABC中, ∠C=90°, AD平分∠BAC, DE⊥AB于E. 给出下列结论:
①DC=DE;
②DA平分∠CDE;
③DE平分∠ADB;
④BE+AC=AB;
⑤∠BAC=∠BDE.
其中正确的是_________(写序号).
热身练习
①②④⑤
方法总结
垂直平分线 ----点向线段两端连线段
当缺少运用角平分线、线段垂直平分线的定理及逆定理的
基本图形时,要添置辅助线 构造 它们的基本图形.
角平分线 ---- 点向角的两边作垂线段
典型例题
3
1.已知:如图,在△ABC中,AB、AC的垂直平分线l1,l2相交于点O. 求证:点O在BC的垂直平分线上.
B
A
C
O
证明:连接OA、OB、OC
∵点O在AB的垂直平分线上.
∴OA=OB
同理OA=OC
∴OC=OB
∴点O在BC的垂直平分线上.
蕴含的知识点:
例题精讲
证明线段相等
A
B
C
P
a
b
c
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
三条边的垂直平分线的性质定理
文字语言:
线段的垂直平分线
三角形
性质定理
逆定理
2.已知:如图,在△ABC中, ∠ABC、∠ACB的平分线BM、CN相交于点P. 求证:点P在∠A的平分线上.
蕴含的知识点:
例题精讲
A
C
B
N
D
F
M
E
P
三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
三个内角平分线的性质定理
文字语言:
角平分线
三角形
性质定理
逆定理
证明线段相等
A
C
B
N
D
F
M
E
P
Q
例题精讲
例题精讲
例题精讲
例题精讲
【答案】2α-180°或180°-2α
4.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
例题精讲
课堂小结
4
B
A
D
O
P
E
A
C
B
P
M
N
∵ OP 是∠AOB 的平分线
PD⊥OA , PE⊥OB
∴PD=PE
性质定理
∵ PD=PE
PD⊥OA , PE⊥OB
∴点P 在∠AOB 的平分线上
逆定理
∵MN⊥AB,AC=BC,
P是MN上任意一点
∴PA=PB
性质定理
∵PA=PB(已知),
∴点P在AB的垂直平分线上
逆定理
确定点
的位置
轴对称图形
证明线
段相等
类比思想
课堂小结
再见
线段、角的轴对称性
线段的轴对称性
1
1.线段的轴对称性
知识点复习:
线段的对称轴
线段垂直平分线的判定
线段是轴对称图形,线段的垂直平分线是它的对称轴.
到线段两端距离相等的点,在这条线段的垂直平分线上.
线段的垂直平分线上的点到线段两端的距离相等.
线段垂直平分线的性质
逆定理
性质定理
文字语言:
文字语言:
线段垂直平分线上
的点到这条线段两
个端点距离相等.
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
C
B
P
M
N
符号语言:
符号语言:
∵MN是AB的垂直平分线∴PA=PB
∵PA=PB
∴点P在AB的垂直平分线上
线段的垂直平分线
热身练习
1.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长等于( )
A.12 B.10 C.8 D.6
B
2.如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A的度数为( )
A.31° B.62° C.87° D.93°
C
角的轴对称性
2
2.角的轴对称性
角的对称轴
角平分线的判定
角是轴对称图形,角平分线所在直线是它的对称轴.
知识点复习:
角平分线上的点到角的两边距离相等.
角平分线的性质
到角的两边距离相等的点,在这个角的平分线上.
注意: 不能写角平分线因为对称轴指的是直线
逆定理
性质定理
文字语言:
文字语言:
角的平分线上的
点到角的两边的
距离相等.
符号语言:
符号语言:
B
A
D
O
P
E
在一个角的内部,且到角的
两边距离相等的点,在这个
角的平分线上.
∵ PD=PE,PD⊥OA , PE⊥OB
∴点P 在∠AOB 的平分线上
角平分线
∵ OP 是∠AOB 的平分线,
PD⊥OA , PE⊥OB
∴PD=PE
1.如图,在△ABC中,∠C = 90°,AD平分∠BAC,CD = 5,则点D到AB的距离为 .
5
2.如图, △ABC中, ∠C=90°, AD平分∠BAC, DE⊥AB于E. 给出下列结论:
①DC=DE;
②DA平分∠CDE;
③DE平分∠ADB;
④BE+AC=AB;
⑤∠BAC=∠BDE.
其中正确的是_________(写序号).
热身练习
①②④⑤
方法总结
垂直平分线 ----点向线段两端连线段
当缺少运用角平分线、线段垂直平分线的定理及逆定理的
基本图形时,要添置辅助线 构造 它们的基本图形.
角平分线 ---- 点向角的两边作垂线段
典型例题
3
1.已知:如图,在△ABC中,AB、AC的垂直平分线l1,l2相交于点O. 求证:点O在BC的垂直平分线上.
B
A
C
O
证明:连接OA、OB、OC
∵点O在AB的垂直平分线上.
∴OA=OB
同理OA=OC
∴OC=OB
∴点O在BC的垂直平分线上.
蕴含的知识点:
例题精讲
证明线段相等
A
B
C
P
a
b
c
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
三条边的垂直平分线的性质定理
文字语言:
线段的垂直平分线
三角形
性质定理
逆定理
2.已知:如图,在△ABC中, ∠ABC、∠ACB的平分线BM、CN相交于点P. 求证:点P在∠A的平分线上.
蕴含的知识点:
例题精讲
A
C
B
N
D
F
M
E
P
三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
三个内角平分线的性质定理
文字语言:
角平分线
三角形
性质定理
逆定理
证明线段相等
A
C
B
N
D
F
M
E
P
Q
例题精讲
例题精讲
例题精讲
例题精讲
【答案】2α-180°或180°-2α
4.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
例题精讲
课堂小结
4
B
A
D
O
P
E
A
C
B
P
M
N
∵ OP 是∠AOB 的平分线
PD⊥OA , PE⊥OB
∴PD=PE
性质定理
∵ PD=PE
PD⊥OA , PE⊥OB
∴点P 在∠AOB 的平分线上
逆定理
∵MN⊥AB,AC=BC,
P是MN上任意一点
∴PA=PB
性质定理
∵PA=PB(已知),
∴点P在AB的垂直平分线上
逆定理
确定点
的位置
轴对称图形
证明线
段相等
类比思想
课堂小结
再见
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
