3.2.1直线、射线、线段(第1课时)[上学期]
文档属性
| 名称 | 3.2.1直线、射线、线段(第1课时)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 50.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-25 18:48:00 | ||
图片预览








文档简介
课件23张PPT。3.2.1直线、射线、线段——直线、射线、线段的概念泗阳县新阳中学 初一数学组本节课你要掌握以下技能1、 理解两点确定一条直线的事实。
2、掌握直线、射线、线段的表示方法。
3、理解直线、射线、线段的联系和区别。
4、通过对直线、射线、线段的研究,体会它们在解决实际问题中的作用,并能用它们解释生活中的一些现象。本节课的重、难点重点:
理解并且会应用“两点确定一条直线”
难点:
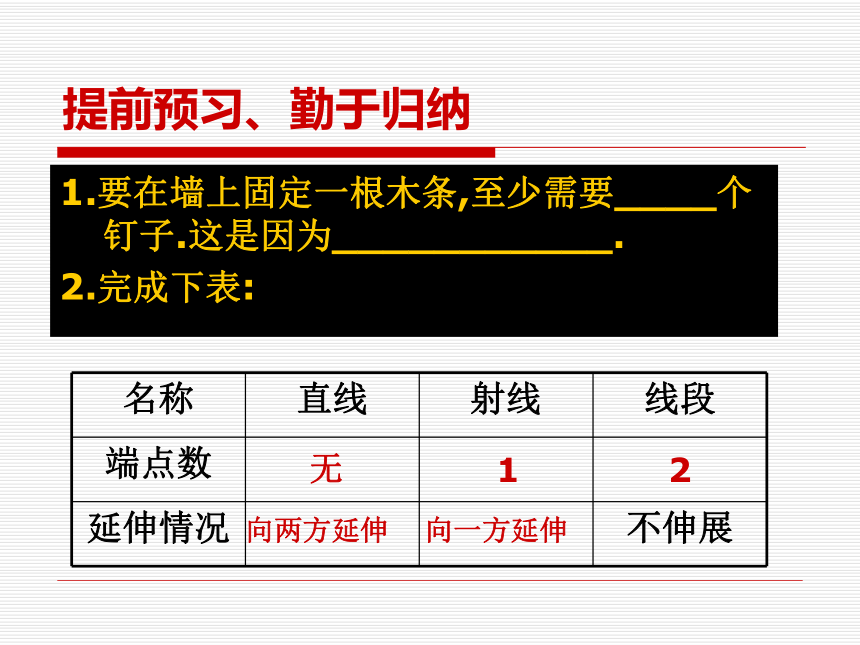
几何语言与几何图形之间的转化。提前预习、勤于归纳1.要在墙上固定一根木条,至少需要____个钉子.这是因为___________.
2.完成下表:
无12向两方延伸向一方延伸3.如图,在直线AB上有四个点分别是A、B、C、D, 则图中共有射线_____条,线段____条,射线AB还可以表示为____(至少写2种).
4.平面内有任何三点都不在一条直线的四个点,过其中的两点共可以画_____直线.提前预习、勤于归纳ABCD86AC、AD6温故知新、查漏补缺一、直线的性质
探究
1、如图(1),要在墙上固定一根木条,至少需要几个钉子?.O.B.A图(1)图(2)2、如图(2),经过一点O画直线,能画出几条?经过两点A、B呢?经过上述的探究你能得出直线的性质吗?经过两点有一条直线,并且只有一条直线。
或者说:两点确定一条直线。二、射线的概念:直线上的一点将直线分成两部分,其中一部分就是射线。如图(1)三、线段的概念:直线上任意两点间的部分。如图(2)图(1)图(2)四、直线、射线、线段的表示方法1、直线有两种表示方法:
(1)可用直线上任意两点的大写字母表示如图(1),表示为直线AB或直线BA(字母是无序的);
(2)也可用一个小写字母表示,如图(2)表示为直线l.图(1)图(2)ABl2、射线有两种表示方法:
可以用端点字母和射线上任意一点的字母来表示,表示端点的字母必须写在前面,字母是有序的,如图,也可以用一个小写字母表示,如射线OA或射l.四、直线、射线、线段的表示方法OAl3、线段也有两种表示方法:
可以用表示端点的两个大写字母表示,也可以用一个小写字母表示,线段AB或直线BA(字母是无序的),直线l.四、直线、射线、线段的表示方法ABa五、直线、射线、线段之间的联系射线和直线都是由线段无限延长形成的。把线段向一个方向无限延长就开成了射线;把线段向两个方向延长就形成了直线;线段、射线也可以都看作是直线的一部分。六、点与线的关系:
线是由无数个点组成的,平面内点与线有两种关系: (1)点在线上;(2)点在线外;
两条直线相交只有一个交点.能力提升1.经过三点中的任意两点作直线,总共可以作
( )
A.一条直线 B.两条直线
C.三条直线 D.一条或三条直线
2.下列说法正确的是 ( )
A.延长直线AB B.延长射线AB
C.延长线段AB D.延伸线段ABDC3.下列写法正确的是( ) A.直线a、b相交于e B.直线AB、CD相交于点E C.直线ab、cd相交于点A D.直线AB、CD相交于点m4.下列说法正确的是 ( )
A.延长直线AB到C,使BC=AB/2
B.延长线段AB到C,使BC=AC
C.延长线段AB到C,使BC=AB/2
D.延长线段BA到C,使BC=ABBC5.三条直线两两相交,交点的个数是________.6.如图,图中共有_____条直线,____条射线,______条线段.ABCD7.如图,(1)图中经过D点的直线有______条,它们是_________.
(2)图中以A为端点的射线有_____条,它们是________________.ABCDFE一863AD、CD、BD4AF、AB、AC、AD7.如图ABCD(1)AC=______+______;
(2)AC=______-______;
(3)BC=______-______;
(4)BC+CD=__________;
(5)CD=AD-__________.AB BCAD CDAC AB(或者BD-CD)BDAC8.判断下列说法是否正确(1)延长直线AB到C. ( )
(2)因为射线是直线的一部分,所以直线比射线长( )
(3)三条直线两两相交,一定有三个交点.( )
(4)一条线段分别向两个方向延长就可以得到直线. ( )
(5)如果两条直线有两个公共点,那么这两条直线一定重合. ( )
(6)两条直线相交,有且只有一个交点.( )×××动手探索1.先画草图,回答问题:
过两点最多能画_____条直线;
过三点最多能画_____条直线;
过同一平面上的四点最多能画____条直线.
那么,过同一平面上的5点呢?6点呢?一条三条六条十条和十五条2.再找规律,填写下表:2×123×224×323.根据以上规律,你能快速地求出过同一平面上的10个点,最多能画几条直线吗?10条15条n×(n-1)25×426×52联系生活 能力提升1.数下列图中线段的总数:
(1)如图1,线段的总数是2+1=3条.ACBACDB图1图2(2)如图2,线段总数是3+2+1=6条.(3)如图3,线段的总数是4+3+2+1=10条, ……ACDB图3E(4)如图4,线段的总条数是____条. 根据以上求线段的总条数的规律:当线段上共有n个点(包括两个端点)时,线段的总条数表示为_____,利用以上规律,当n=22时,线段的总数是______条. 由以上规律,你知道,如果10位同学聚会,互相握手致意,每个人要握多少次手?一共需要握多少次手?10个队进行蓝球循环赛,共要赛多少场?10个同学在元旦节互送卡片,一共要多少张?DACEFB图415n×(n-1)22312.(1)在同一个平面内,两条直线相交,只有____个交点. (2)在同一个平面内,三条直线两两相交,则交点最多有___个. (3)在同一个平面内,四条直线两两相交,则交点最多有____个. (4)在同一平面内,十条直线两两相交,则交点最多有____个. n个点呢?体会上述三题之间的共同规律是什么?13645n×(n-1)2总结与反思通过本节课的学习,你对直线、射线、线段有了一个更新的认识了吧,请与同学们交流一下,谈谈自已的体会。作业布置一、课堂作业:
课本P126习题3.2第2、3、4题;
二、课外作业:
1、课本P124练习;
2、补充习题及课时作业上面的有关习题;
3、预习课本P124-125中的内容。
2、掌握直线、射线、线段的表示方法。
3、理解直线、射线、线段的联系和区别。
4、通过对直线、射线、线段的研究,体会它们在解决实际问题中的作用,并能用它们解释生活中的一些现象。本节课的重、难点重点:
理解并且会应用“两点确定一条直线”
难点:
几何语言与几何图形之间的转化。提前预习、勤于归纳1.要在墙上固定一根木条,至少需要____个钉子.这是因为___________.
2.完成下表:
无12向两方延伸向一方延伸3.如图,在直线AB上有四个点分别是A、B、C、D, 则图中共有射线_____条,线段____条,射线AB还可以表示为____(至少写2种).
4.平面内有任何三点都不在一条直线的四个点,过其中的两点共可以画_____直线.提前预习、勤于归纳ABCD86AC、AD6温故知新、查漏补缺一、直线的性质
探究
1、如图(1),要在墙上固定一根木条,至少需要几个钉子?.O.B.A图(1)图(2)2、如图(2),经过一点O画直线,能画出几条?经过两点A、B呢?经过上述的探究你能得出直线的性质吗?经过两点有一条直线,并且只有一条直线。
或者说:两点确定一条直线。二、射线的概念:直线上的一点将直线分成两部分,其中一部分就是射线。如图(1)三、线段的概念:直线上任意两点间的部分。如图(2)图(1)图(2)四、直线、射线、线段的表示方法1、直线有两种表示方法:
(1)可用直线上任意两点的大写字母表示如图(1),表示为直线AB或直线BA(字母是无序的);
(2)也可用一个小写字母表示,如图(2)表示为直线l.图(1)图(2)ABl2、射线有两种表示方法:
可以用端点字母和射线上任意一点的字母来表示,表示端点的字母必须写在前面,字母是有序的,如图,也可以用一个小写字母表示,如射线OA或射l.四、直线、射线、线段的表示方法OAl3、线段也有两种表示方法:
可以用表示端点的两个大写字母表示,也可以用一个小写字母表示,线段AB或直线BA(字母是无序的),直线l.四、直线、射线、线段的表示方法ABa五、直线、射线、线段之间的联系射线和直线都是由线段无限延长形成的。把线段向一个方向无限延长就开成了射线;把线段向两个方向延长就形成了直线;线段、射线也可以都看作是直线的一部分。六、点与线的关系:
线是由无数个点组成的,平面内点与线有两种关系: (1)点在线上;(2)点在线外;
两条直线相交只有一个交点.能力提升1.经过三点中的任意两点作直线,总共可以作
( )
A.一条直线 B.两条直线
C.三条直线 D.一条或三条直线
2.下列说法正确的是 ( )
A.延长直线AB B.延长射线AB
C.延长线段AB D.延伸线段ABDC3.下列写法正确的是( ) A.直线a、b相交于e B.直线AB、CD相交于点E C.直线ab、cd相交于点A D.直线AB、CD相交于点m4.下列说法正确的是 ( )
A.延长直线AB到C,使BC=AB/2
B.延长线段AB到C,使BC=AC
C.延长线段AB到C,使BC=AB/2
D.延长线段BA到C,使BC=ABBC5.三条直线两两相交,交点的个数是________.6.如图,图中共有_____条直线,____条射线,______条线段.ABCD7.如图,(1)图中经过D点的直线有______条,它们是_________.
(2)图中以A为端点的射线有_____条,它们是________________.ABCDFE一863AD、CD、BD4AF、AB、AC、AD7.如图ABCD(1)AC=______+______;
(2)AC=______-______;
(3)BC=______-______;
(4)BC+CD=__________;
(5)CD=AD-__________.AB BCAD CDAC AB(或者BD-CD)BDAC8.判断下列说法是否正确(1)延长直线AB到C. ( )
(2)因为射线是直线的一部分,所以直线比射线长( )
(3)三条直线两两相交,一定有三个交点.( )
(4)一条线段分别向两个方向延长就可以得到直线. ( )
(5)如果两条直线有两个公共点,那么这两条直线一定重合. ( )
(6)两条直线相交,有且只有一个交点.( )×××动手探索1.先画草图,回答问题:
过两点最多能画_____条直线;
过三点最多能画_____条直线;
过同一平面上的四点最多能画____条直线.
那么,过同一平面上的5点呢?6点呢?一条三条六条十条和十五条2.再找规律,填写下表:2×123×224×323.根据以上规律,你能快速地求出过同一平面上的10个点,最多能画几条直线吗?10条15条n×(n-1)25×426×52联系生活 能力提升1.数下列图中线段的总数:
(1)如图1,线段的总数是2+1=3条.ACBACDB图1图2(2)如图2,线段总数是3+2+1=6条.(3)如图3,线段的总数是4+3+2+1=10条, ……ACDB图3E(4)如图4,线段的总条数是____条. 根据以上求线段的总条数的规律:当线段上共有n个点(包括两个端点)时,线段的总条数表示为_____,利用以上规律,当n=22时,线段的总数是______条. 由以上规律,你知道,如果10位同学聚会,互相握手致意,每个人要握多少次手?一共需要握多少次手?10个队进行蓝球循环赛,共要赛多少场?10个同学在元旦节互送卡片,一共要多少张?DACEFB图415n×(n-1)22312.(1)在同一个平面内,两条直线相交,只有____个交点. (2)在同一个平面内,三条直线两两相交,则交点最多有___个. (3)在同一个平面内,四条直线两两相交,则交点最多有____个. (4)在同一平面内,十条直线两两相交,则交点最多有____个. n个点呢?体会上述三题之间的共同规律是什么?13645n×(n-1)2总结与反思通过本节课的学习,你对直线、射线、线段有了一个更新的认识了吧,请与同学们交流一下,谈谈自已的体会。作业布置一、课堂作业:
课本P126习题3.2第2、3、4题;
二、课外作业:
1、课本P124练习;
2、补充习题及课时作业上面的有关习题;
3、预习课本P124-125中的内容。
