24.1.2 垂直于弦的直径基础卷 (含答案)
文档属性
| 名称 | 24.1.2 垂直于弦的直径基础卷 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 460.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 00:00:00 | ||
图片预览



文档简介
24.1.2 垂直于弦的直径(基础卷)-人教版九年级上册(含答案)
一.选择题
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O的半径的长是( )
A.5 B.4 C.3 D.2
2.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A.10cm B.15cm C.20cm D.24cm
3.如图,在⊙O中,直径AB=8,弦DE⊥AB于点C,若AD=DE,则BC的长为( )
A. B. C.1 D.2
4.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )
A. B.4 C. D.5
5.往圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,水的最大深度为16cm,则圆柱形容器的截面直径为( )cm.
A.10 B.14 C.26 D.52
6.一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B. C. D.
7.把半径长为2.5的球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知CD=4,则EF=( )
A.2 B.2.5 C.4 D.5
8.如图,点A,C,D均在⊙O上,点B在⊙O内,且AB⊥BC于点B,BC⊥CD于点C,若AB=4,BC=8,CD=2,则⊙O的面积为( )
A. B. C. D.
9.如图,在⊙O中,弦AB=5,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为( )
A.5 B.2.5 C.3 D.2
10.如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,在点P运动的过程中,OQ的长度为( )
A.1 B.1.5 C.2 D.不能确定
二.填空题
.如图,在⊙O中,弦AB⊥OC于E点,C在圆上,AB=8,CE=2,则⊙O的半径AO= .
.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 .(结果保留π)
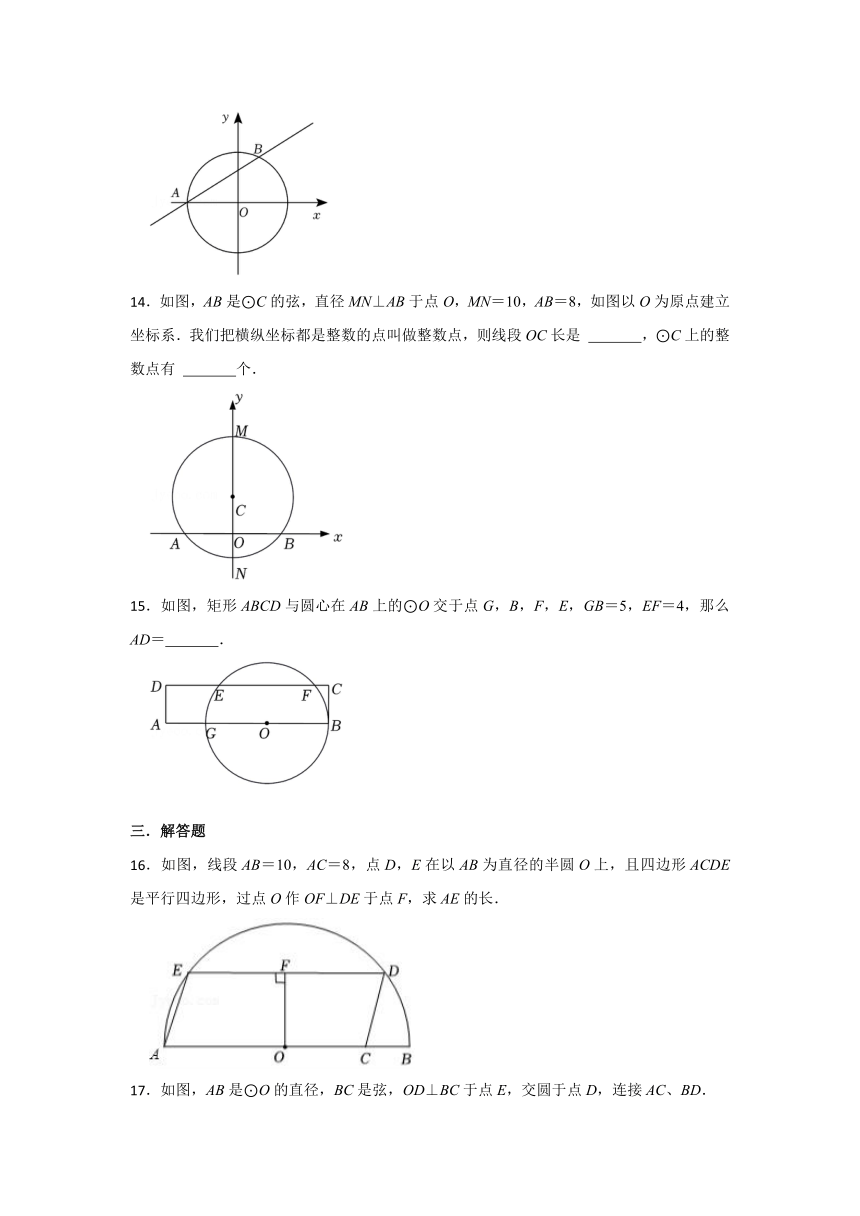
.如图,在平面直角坐标系xOy中,直线y=与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
.如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,如图以O为原点建立坐标系.我们把横纵坐标都是整数的点叫做整数点,则线段OC长是 ,⊙C上的整数点有 个.
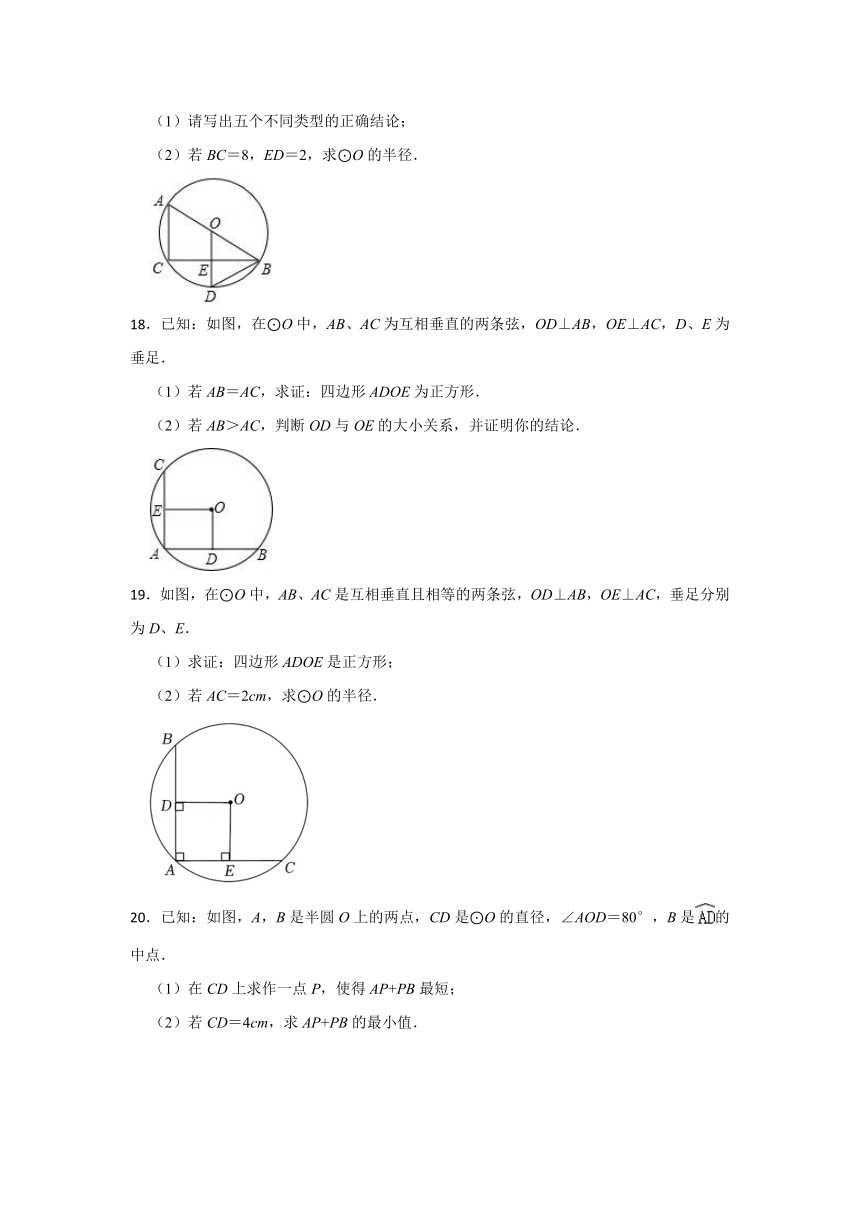
.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= .
三.解答题
.如图,线段AB=10,AC=8,点D,E在以AB为直径的半圆O上,且四边形ACDE是平行四边形,过点O作OF⊥DE于点F,求AE的长.
.如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交圆于点D,连接AC、BD.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
.已知:如图,在⊙O中,AB、AC为互相垂直的两条弦,OD⊥AB,OE⊥AC,D、E为垂足.
(1)若AB=AC,求证:四边形ADOE为正方形.
(2)若AB>AC,判断OD与OE的大小关系,并证明你的结论.
.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E.
(1)求证:四边形ADOE是正方形;
(2)若AC=2cm,求⊙O的半径.
.已知:如图,A,B是半圆O上的两点,CD是⊙O的直径,∠AOD=80°,B是的中点.
(1)在CD上求作一点P,使得AP+PB最短;
(2)若CD=4cm,求AP+PB的最小值.
参考答案与试题解析
一.选择题
1.【解答】解:连接OC,
设⊙O的半径为R,则OE=8﹣R,
∵CD⊥AB,AB过圆心O,CD=8,
∴∠OEC=90°,CE=DE=4,
由勾股定理得:OC2=CE2+OE2,
R2=42+(8﹣R)2,
解得:R=5,
即⊙O的半径长是5,
故选:A.
2.【解答】解:如图,连接OE,交AB于点F,连接OA,
∵AC⊥CD、BD⊥CD,
∴AC∥BD,
∵AC=BD=4cm,
∴四边形ACDB是平行四边形,
∴四边形ACDB是矩形,
∴AB∥CD,AB=CD=16cm,
∵CD切⊙O于点E,
∴OE⊥CD,
∴OE⊥AB,
∴四边形EFBD是矩形,AF=AB=×16=8(cm),
∴EF=BD=4cm,
设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,
在Rt△AOF中,OA2=AF2+OF2,
∴r2=82+(r﹣4)2,
解得:r=10,
∴这种铁球的直径为20cm,
故选:C.
3.【解答】解:∵DE⊥AB,AB过圆心O,
∴DC=CE=DE,∠ACD=∠BCD=90°,
∵AD=DE,
∴DC=AD,
∴∠DAC=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD=AB==4,
∵∠ADB=90°,∠DAB=30°,
∴∠ABD=60°,
∵∠DCB=90°,
∴∠CDB=30°,
∴BC=BD=,
故选:D.
4.【解答】解:如图,过点O作OC⊥AB于点C,连接OB,
则OB=7,
∵PA=4,PB=6,
∴AB=PA+PB=10,
∵OC⊥AB,
∴AC=BC=5,
∴PC=PB﹣BC=1,
在Rt△OBC中,根据勾股定理得:
OC2=OB2﹣BC2=72﹣52=24,
在Rt△OPC中,根据勾股定理得:
OP===5,
故选:D.
5.【解答】解:如图所示:
由题意得,OC⊥AB于D,DC=16cm,
∵AB=48cm,
∴BD=AB=×48=24(cm),
设半径为rcm,则OD=(r﹣16)cm,
在Rt△OBD中,
r2=242+(r﹣16)2,解得r=26,
所以2r=52,
故选:D.
6.【解答】解:连接OA,OB,如图,
根据题意得:OA=6cm,弦心距OC=3cm,
∴cos∠AOC=,
∴∠AOC=60°,则∠AOB=120°,
∴AC=3cm,AB=2AC=6cm,
∴S阴影=S扇形OAB﹣S△OAB=.
设把该容器扶正竖直后容器中液体的高度为h,
依题意得:,
∴,
故选:B.
7.【解答】解:设球的平面投影圆心为O,过点O作ON⊥AD于点N,延长NO交BC于点M,连接OF,如图所示:
则NF=EN=EF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDNM是矩形,
∴MN=CD=4,ON=MN﹣OM=4﹣2.5=1.5,
在Rt△ONF中,由勾股定理得:ON2+NF2=OF2,
∴NF==2,EF=2NF=4,
故选:C.
8.【解答】解:如图,连接OA、OC,过点O作OM⊥CD于M,MO的延长线于AB延长线交于N,则四边形BCMN是矩形,
∵OM⊥CD,CD是弦,
∴CM=DM=CD=1=BN,
∴AN=AB+BN=4+1=5,
设ON=x,则OM=8﹣x,
在Rt△AON、Rt△COM中,由勾股定理得,
OA2=AN2+ON2,OC2=OM2+CM2,
∵OA=OC,
∴AN2+ON2=OM2+CM2,
即52+x2=(8﹣x)2+12,
解得x=,
即ON=,
∴OA2=52+()2=,
∴S⊙O=π×OA2=π,
故选:A.
9.【解答】解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90°,
∴CD=,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=×5=2.5,
即CD的最大值为2.5,
故选:B.
10.【解答】解:连接OP,PQ,则OP=2,
∵AB⊥CD,PM⊥OA,PN⊥OD,
∴∠MON=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP=2,
∵∠MON=90°,Q为MN中点,
∴OQ=MN==1,
故选:A.
二.填空题
.【解答】解:设OA=OC=r,
∵OC⊥AB,OC是半径,
∴AE=EB=4,
在Rt△AEO中,OA2=AE2+OE2,
∴r2=42+(r﹣2)2,
∴r=5.
故答案为:5.
.【解答】解:如图,连接OB,过点O作OD⊥AB于D,
∵OD⊥AB,OD过圆心,AB是弦,
∴AD=BD=AB=(AC+BC)=×(11+21)=16,
∴CD=BC﹣BD=21﹣16=5,
在Rt△COD中,OD2=OC2﹣CD2=132﹣52=144,
在Rt△BOD中,OB2=OD2+BD2=144+256=400,
∴S⊙O=π×OB2=400π,
故答案为:400π.
.【解答】解:过O作OM⊥直线AB与M,直线AB交y轴于C,
y=,
当x=0时,y=,
当y=0时,x+=0,解得:x=﹣3,
所以OC=,OA=3,
∵tan∠CAO==,
∴∠CAO=30°,
∵OM⊥AC,
∴∠OMA=90°,
∴OM=OA=,
由勾股定理得:AM===,
∵OM⊥AB,OM过圆心O,
∴AM=BM=,
∴AB=AM+BM=+=3,
故答案为:3.
.【解答】解:过C作直径UL∥x轴,
连接CA,则AC=×10=5,
∵MN过圆心C,MN⊥AB,AB=8,
∴AO=BO=4,∠AOC=90°,
由勾股定理得:CO===3,
∴ON=5﹣3=2,OM=5+3=8,
即A(﹣4,0),B(4,0),M(0,8),N(0,﹣2),
同理还有弦QR=AB=8,弦WE=TS=6,且WE、TS、QR都平行于x轴,
Q(﹣4,6),R(4,6),W(﹣3,7),E(3,7),T(﹣3,﹣1),S(3,﹣1),U(﹣5,3),L(5,3),
即共12个点,
故答案为:3;12.
.【解答】解:过O作OM⊥EF于M,连接OE,则∠OMD=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴四边形AOMD是矩形,
∴OM=AD,
∵OM⊥EF,OM过圆心O,EF=4,
∴EM=FM=2,
∵OG=OB,BG=5,
∴OB=OG=2.5=OE,
在Rt△OME中,由勾股定理得:OM===1.5,
∴AD=OM=1.5,
故答案为:1.5.
三.解答题
.【解答】解:过点E作EG⊥AB于点G,连接OE,则OE=OA=,∠EGO=90°,
∵四边形ACDE是平行四边形,
∴DE=AC=8,DE∥AB,
∵OF⊥DE,即∠OFE=90°,
∴EF==4,∠FOG=∠OFE=90°,
∴四边形OFEG是矩形,
∴OG=EF=4,
∴AG=5﹣4=1,
在Rt△OEG中,EG=,
在Rt△AGE中,AE=.
.【解答】解:(1)正确的结论有:CE=BE,=,OE=AC,∠C=90°,AC∥OD;
(2)∵OD⊥BC,OD过圆心O,BC=8,
∴∠OEB=90°,BE=CE=4,
设⊙O的半径为R,则OB=OD=R,
由勾股定理得:OB2=OE2+BE2,
即R2=(R﹣2)2+42,
解得:R=5,
即⊙O的半径是5.
.【解答】(1)证明:连接OA,
∵OD⊥AB,OE⊥AC,OD和OE都过圆心O,
∴∠OEA=∠ODA=90°,AE=CE,AD=BD,
∵AC=AB,
∴AE=AD,
∵AB、AC为互相垂直的两条弦,
∴∠EAD=90°,
即∠OEA=∠EAD=∠ODA=90°,
∴四边形EADO是正方形(有一组邻边相等的矩形是正方形);
(2)解:OD<OE,
证明:∵AB>AC,AE=CE,AD=BD,
∴AD>AE,
在Rt△ODA和Rt△OEA中,由勾股定理得:
OE2=OA2﹣AE2,OD2=OA2﹣AD2,
∴OD2<OE2,
即OD<OE.
.【解答】(1)证明:∵OD⊥AB,OE⊥AC,
∴AD=AB,AE=AC,
∵AB=AC,
∴AD=AE,
∵∠ADO=∠A=∠AEO=90°,
∴四边形ADOE是正方形;
(2)解:连接OA,
∵AC=2cm,
∴AE=1cm,
在Rt△AOE中,OA==(cm),
答:⊙O的半径是cm.
.【解答】解:(1)作BB′⊥CD,交圆于B′,然后连接AB′,交CD于P点,P就是所求的点;
(2)延长AO交圆于E,连接OB′,B′E.
∵BB′⊥CD
∴=,
∵∠AOD=80°,B是的中点,
∴∠DOB′=∠AOD=40°.
∴∠AOB′=∠AOD+∠DOB′=120°,
又∵OA=OB′,
∴∠A==30°.
∵AE是圆的直径,
∴∠AB′E=90°,
∴直角△AEB′中,B′E=AE=×4=2,
∴AB′===2cm.
一.选择题
1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O的半径的长是( )
A.5 B.4 C.3 D.2
2.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A.10cm B.15cm C.20cm D.24cm
3.如图,在⊙O中,直径AB=8,弦DE⊥AB于点C,若AD=DE,则BC的长为( )
A. B. C.1 D.2
4.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )
A. B.4 C. D.5
5.往圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,水的最大深度为16cm,则圆柱形容器的截面直径为( )cm.
A.10 B.14 C.26 D.52
6.一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B. C. D.
7.把半径长为2.5的球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知CD=4,则EF=( )
A.2 B.2.5 C.4 D.5
8.如图,点A,C,D均在⊙O上,点B在⊙O内,且AB⊥BC于点B,BC⊥CD于点C,若AB=4,BC=8,CD=2,则⊙O的面积为( )
A. B. C. D.
9.如图,在⊙O中,弦AB=5,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为( )
A.5 B.2.5 C.3 D.2
10.如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,在点P运动的过程中,OQ的长度为( )
A.1 B.1.5 C.2 D.不能确定
二.填空题
.如图,在⊙O中,弦AB⊥OC于E点,C在圆上,AB=8,CE=2,则⊙O的半径AO= .
.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 .(结果保留π)
.如图,在平面直角坐标系xOy中,直线y=与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
.如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,如图以O为原点建立坐标系.我们把横纵坐标都是整数的点叫做整数点,则线段OC长是 ,⊙C上的整数点有 个.
.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=5,EF=4,那么AD= .
三.解答题
.如图,线段AB=10,AC=8,点D,E在以AB为直径的半圆O上,且四边形ACDE是平行四边形,过点O作OF⊥DE于点F,求AE的长.
.如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交圆于点D,连接AC、BD.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
.已知:如图,在⊙O中,AB、AC为互相垂直的两条弦,OD⊥AB,OE⊥AC,D、E为垂足.
(1)若AB=AC,求证:四边形ADOE为正方形.
(2)若AB>AC,判断OD与OE的大小关系,并证明你的结论.
.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E.
(1)求证:四边形ADOE是正方形;
(2)若AC=2cm,求⊙O的半径.
.已知:如图,A,B是半圆O上的两点,CD是⊙O的直径,∠AOD=80°,B是的中点.
(1)在CD上求作一点P,使得AP+PB最短;
(2)若CD=4cm,求AP+PB的最小值.
参考答案与试题解析
一.选择题
1.【解答】解:连接OC,
设⊙O的半径为R,则OE=8﹣R,
∵CD⊥AB,AB过圆心O,CD=8,
∴∠OEC=90°,CE=DE=4,
由勾股定理得:OC2=CE2+OE2,
R2=42+(8﹣R)2,
解得:R=5,
即⊙O的半径长是5,
故选:A.
2.【解答】解:如图,连接OE,交AB于点F,连接OA,
∵AC⊥CD、BD⊥CD,
∴AC∥BD,
∵AC=BD=4cm,
∴四边形ACDB是平行四边形,
∴四边形ACDB是矩形,
∴AB∥CD,AB=CD=16cm,
∵CD切⊙O于点E,
∴OE⊥CD,
∴OE⊥AB,
∴四边形EFBD是矩形,AF=AB=×16=8(cm),
∴EF=BD=4cm,
设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,
在Rt△AOF中,OA2=AF2+OF2,
∴r2=82+(r﹣4)2,
解得:r=10,
∴这种铁球的直径为20cm,
故选:C.
3.【解答】解:∵DE⊥AB,AB过圆心O,
∴DC=CE=DE,∠ACD=∠BCD=90°,
∵AD=DE,
∴DC=AD,
∴∠DAC=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD=AB==4,
∵∠ADB=90°,∠DAB=30°,
∴∠ABD=60°,
∵∠DCB=90°,
∴∠CDB=30°,
∴BC=BD=,
故选:D.
4.【解答】解:如图,过点O作OC⊥AB于点C,连接OB,
则OB=7,
∵PA=4,PB=6,
∴AB=PA+PB=10,
∵OC⊥AB,
∴AC=BC=5,
∴PC=PB﹣BC=1,
在Rt△OBC中,根据勾股定理得:
OC2=OB2﹣BC2=72﹣52=24,
在Rt△OPC中,根据勾股定理得:
OP===5,
故选:D.
5.【解答】解:如图所示:
由题意得,OC⊥AB于D,DC=16cm,
∵AB=48cm,
∴BD=AB=×48=24(cm),
设半径为rcm,则OD=(r﹣16)cm,
在Rt△OBD中,
r2=242+(r﹣16)2,解得r=26,
所以2r=52,
故选:D.
6.【解答】解:连接OA,OB,如图,
根据题意得:OA=6cm,弦心距OC=3cm,
∴cos∠AOC=,
∴∠AOC=60°,则∠AOB=120°,
∴AC=3cm,AB=2AC=6cm,
∴S阴影=S扇形OAB﹣S△OAB=.
设把该容器扶正竖直后容器中液体的高度为h,
依题意得:,
∴,
故选:B.
7.【解答】解:设球的平面投影圆心为O,过点O作ON⊥AD于点N,延长NO交BC于点M,连接OF,如图所示:
则NF=EN=EF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDNM是矩形,
∴MN=CD=4,ON=MN﹣OM=4﹣2.5=1.5,
在Rt△ONF中,由勾股定理得:ON2+NF2=OF2,
∴NF==2,EF=2NF=4,
故选:C.
8.【解答】解:如图,连接OA、OC,过点O作OM⊥CD于M,MO的延长线于AB延长线交于N,则四边形BCMN是矩形,
∵OM⊥CD,CD是弦,
∴CM=DM=CD=1=BN,
∴AN=AB+BN=4+1=5,
设ON=x,则OM=8﹣x,
在Rt△AON、Rt△COM中,由勾股定理得,
OA2=AN2+ON2,OC2=OM2+CM2,
∵OA=OC,
∴AN2+ON2=OM2+CM2,
即52+x2=(8﹣x)2+12,
解得x=,
即ON=,
∴OA2=52+()2=,
∴S⊙O=π×OA2=π,
故选:A.
9.【解答】解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90°,
∴CD=,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=×5=2.5,
即CD的最大值为2.5,
故选:B.
10.【解答】解:连接OP,PQ,则OP=2,
∵AB⊥CD,PM⊥OA,PN⊥OD,
∴∠MON=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP=2,
∵∠MON=90°,Q为MN中点,
∴OQ=MN==1,
故选:A.
二.填空题
.【解答】解:设OA=OC=r,
∵OC⊥AB,OC是半径,
∴AE=EB=4,
在Rt△AEO中,OA2=AE2+OE2,
∴r2=42+(r﹣2)2,
∴r=5.
故答案为:5.
.【解答】解:如图,连接OB,过点O作OD⊥AB于D,
∵OD⊥AB,OD过圆心,AB是弦,
∴AD=BD=AB=(AC+BC)=×(11+21)=16,
∴CD=BC﹣BD=21﹣16=5,
在Rt△COD中,OD2=OC2﹣CD2=132﹣52=144,
在Rt△BOD中,OB2=OD2+BD2=144+256=400,
∴S⊙O=π×OB2=400π,
故答案为:400π.
.【解答】解:过O作OM⊥直线AB与M,直线AB交y轴于C,
y=,
当x=0时,y=,
当y=0时,x+=0,解得:x=﹣3,
所以OC=,OA=3,
∵tan∠CAO==,
∴∠CAO=30°,
∵OM⊥AC,
∴∠OMA=90°,
∴OM=OA=,
由勾股定理得:AM===,
∵OM⊥AB,OM过圆心O,
∴AM=BM=,
∴AB=AM+BM=+=3,
故答案为:3.
.【解答】解:过C作直径UL∥x轴,
连接CA,则AC=×10=5,
∵MN过圆心C,MN⊥AB,AB=8,
∴AO=BO=4,∠AOC=90°,
由勾股定理得:CO===3,
∴ON=5﹣3=2,OM=5+3=8,
即A(﹣4,0),B(4,0),M(0,8),N(0,﹣2),
同理还有弦QR=AB=8,弦WE=TS=6,且WE、TS、QR都平行于x轴,
Q(﹣4,6),R(4,6),W(﹣3,7),E(3,7),T(﹣3,﹣1),S(3,﹣1),U(﹣5,3),L(5,3),
即共12个点,
故答案为:3;12.
.【解答】解:过O作OM⊥EF于M,连接OE,则∠OMD=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴四边形AOMD是矩形,
∴OM=AD,
∵OM⊥EF,OM过圆心O,EF=4,
∴EM=FM=2,
∵OG=OB,BG=5,
∴OB=OG=2.5=OE,
在Rt△OME中,由勾股定理得:OM===1.5,
∴AD=OM=1.5,
故答案为:1.5.
三.解答题
.【解答】解:过点E作EG⊥AB于点G,连接OE,则OE=OA=,∠EGO=90°,
∵四边形ACDE是平行四边形,
∴DE=AC=8,DE∥AB,
∵OF⊥DE,即∠OFE=90°,
∴EF==4,∠FOG=∠OFE=90°,
∴四边形OFEG是矩形,
∴OG=EF=4,
∴AG=5﹣4=1,
在Rt△OEG中,EG=,
在Rt△AGE中,AE=.
.【解答】解:(1)正确的结论有:CE=BE,=,OE=AC,∠C=90°,AC∥OD;
(2)∵OD⊥BC,OD过圆心O,BC=8,
∴∠OEB=90°,BE=CE=4,
设⊙O的半径为R,则OB=OD=R,
由勾股定理得:OB2=OE2+BE2,
即R2=(R﹣2)2+42,
解得:R=5,
即⊙O的半径是5.
.【解答】(1)证明:连接OA,
∵OD⊥AB,OE⊥AC,OD和OE都过圆心O,
∴∠OEA=∠ODA=90°,AE=CE,AD=BD,
∵AC=AB,
∴AE=AD,
∵AB、AC为互相垂直的两条弦,
∴∠EAD=90°,
即∠OEA=∠EAD=∠ODA=90°,
∴四边形EADO是正方形(有一组邻边相等的矩形是正方形);
(2)解:OD<OE,
证明:∵AB>AC,AE=CE,AD=BD,
∴AD>AE,
在Rt△ODA和Rt△OEA中,由勾股定理得:
OE2=OA2﹣AE2,OD2=OA2﹣AD2,
∴OD2<OE2,
即OD<OE.
.【解答】(1)证明:∵OD⊥AB,OE⊥AC,
∴AD=AB,AE=AC,
∵AB=AC,
∴AD=AE,
∵∠ADO=∠A=∠AEO=90°,
∴四边形ADOE是正方形;
(2)解:连接OA,
∵AC=2cm,
∴AE=1cm,
在Rt△AOE中,OA==(cm),
答:⊙O的半径是cm.
.【解答】解:(1)作BB′⊥CD,交圆于B′,然后连接AB′,交CD于P点,P就是所求的点;
(2)延长AO交圆于E,连接OB′,B′E.
∵BB′⊥CD
∴=,
∵∠AOD=80°,B是的中点,
∴∠DOB′=∠AOD=40°.
∴∠AOB′=∠AOD+∠DOB′=120°,
又∵OA=OB′,
∴∠A==30°.
∵AE是圆的直径,
∴∠AB′E=90°,
∴直角△AEB′中,B′E=AE=×4=2,
∴AB′===2cm.
同课章节目录
