2022-2023学年人教版八年级数学上册11.3 多边形及其内角和复习题(含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.3 多边形及其内角和复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 554.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 17:51:50 | ||
图片预览



文档简介
11.3 多边形及其内角和复习题(含答案)-人教版八年级上册
一.选择题
.在计算一个多边形的内角和时,由于粗心少算了1个内角,其和等于1180°,则少算的这个角的度数是( )
A.60° B.70° C.80° D.90°
.一个多边形每个外角都等于36°,则从这个多边形的某个顶点画对角线,最多可以画出几条( )
A.7条 B.8条 C.9条 D.10条
.如图,五边形ABCDE是正五边形,若l1∥l2,则∠1﹣∠2的值是( )
A.108° B.36° C.72° D.144°
.下列叙述正确的有( )个.
①射线AB的端点是A和B;
②各边相等,各角也相等的多边形叫做正多边形;
③连接两点的线段叫做两点的距离;
④两点之间线段最短.
A.1 B.2 C.3 D.4
.四边形ABCD两组对边AD,BC与AB,DC延长线分别交于点E,F,∠AEB,∠AFD的平分线交于点P,∠A=64°,∠BCD=136°,则下列结论中正确的是( )
①∠EPF=100°;②∠ADC+∠ABC=160°;③∠PEB+∠PFC+∠EPF=136°;④∠PEA+∠PFA=36°
A.①②③ B.②③④ C.①③④ D.①②③④
如图,四边形ABCD为一长方形纸带,AD∥BC,将四边形ABCD沿EF折叠,C、D两点分别与C′、D′对应,若∠1=2∠2,则∠3的度数为( )
A.50° B.54° C.58° D.62°
如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α,再沿直线前进8米,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度α为( )
A.30° B.40° C.45° D.60°
如图,在正六边形ABCDEF内作正方形BCGH,连接AH,则∠FAH等于( )
A.75° B.72° C.60° D.45°
若n边形的内角和与外角和相加为1800°,则n的值为( )
A.7 B.8. C.9 D.10
如图,∠A+∠B+∠C+∠D+∠E+∠F=( )
A.180° B.240° C.360° D.540°
二.填空题
.若一个多边形每一个外角都等于36°,则这个多边形有 条边.
.一个正多边形的内角和为720°,则这个正多边形的每一个外角等于 .
.如图所示,分别以n边形顶角顶点为圆心,以2cm长为半径画圆,则圆中阴影部分面积之和为 cm2.
.一个正多边形的每个内角都是144°,则这个多边形的内角和为 .
.如图,小华从点A出发向前走10m,向右转15°,然后继续向前走10m,再向右转15°,他以同样的方法继续走下去,当他第一次回到点A时共走了 m.
解答题
.化简/求解:
(1)若a,b,c是△ABC的三边的长,化简|a﹣b﹣c|+|b﹣c﹣a|+|c+a﹣b|.
(2)已知一正多边形的内角与其相邻的外角的比为3:1,求该多边形的边数.
.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB.
①若∠A=50°,则∠O= ,∠P= ;
②若∠A=α,则∠O= ,∠P= .(用含α的式子表示)
(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P与∠A,∠D的数量关系,并说明理由.
.利用“模型”解决几何综合问题往往会取得事半功倍的效果.
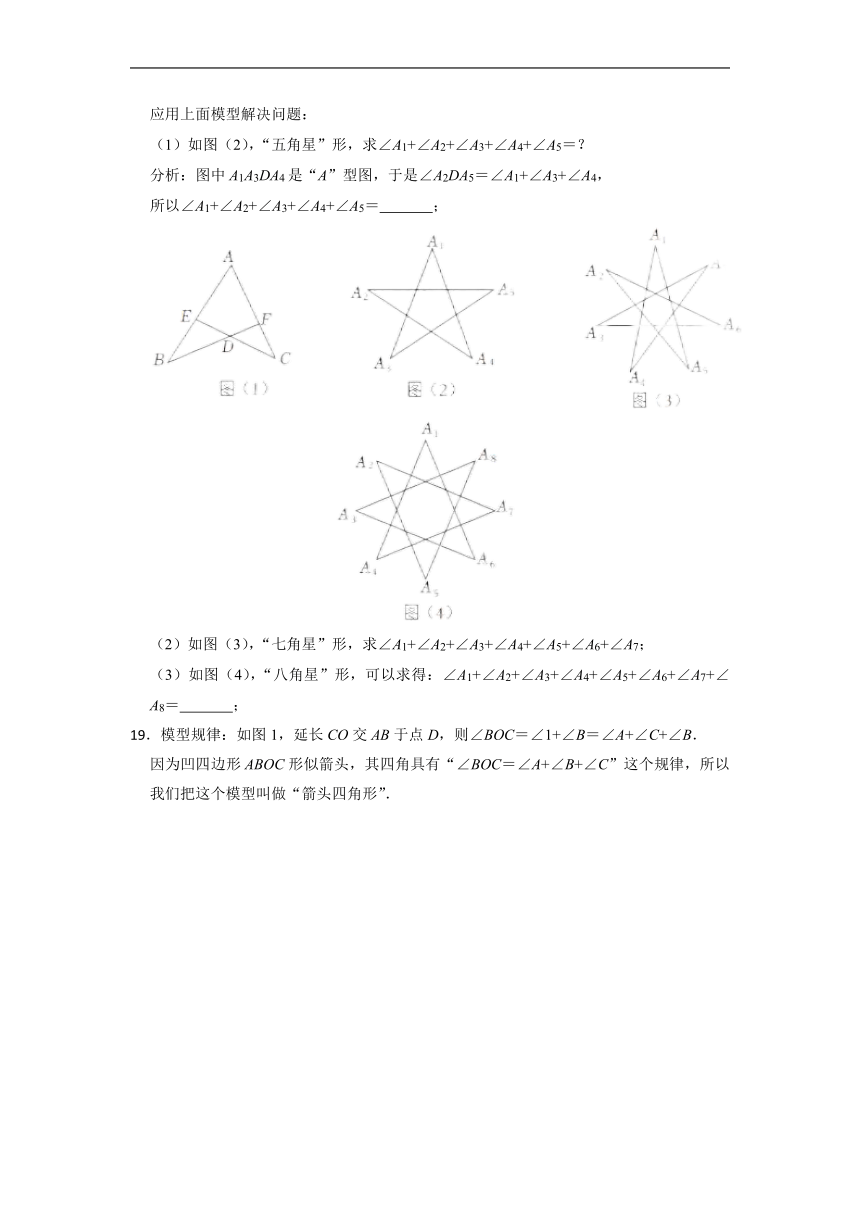
几何模型:如图(1),我们称它为“A”型图案,
易证明:∠EDF=∠A+∠B+∠C;
应用上面模型解决问题:
(1)如图(2),“五角星”形,求∠A1+∠A2+∠A3+∠A4+∠A5=?
分析:图中A1A3DA4是“A”型图,于是∠A2DA5=∠A1+∠A3+∠A4,
所以∠A1+∠A2+∠A3+∠A4+∠A5= ;
(2)如图(3),“七角星”形,求∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7;
(3)如图(4),“八角星”形,可以求得:∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8= ;
.模型规律:如图1,延长CO交AB于点D,则∠BOC=∠1+∠B=∠A+∠C+∠B.
因为凹四边形ABOC形似箭头,其四角具有“∠BOC=∠A+∠B+∠C”这个规律,所以我们把这个模型叫做“箭头四角形”.
模型应用
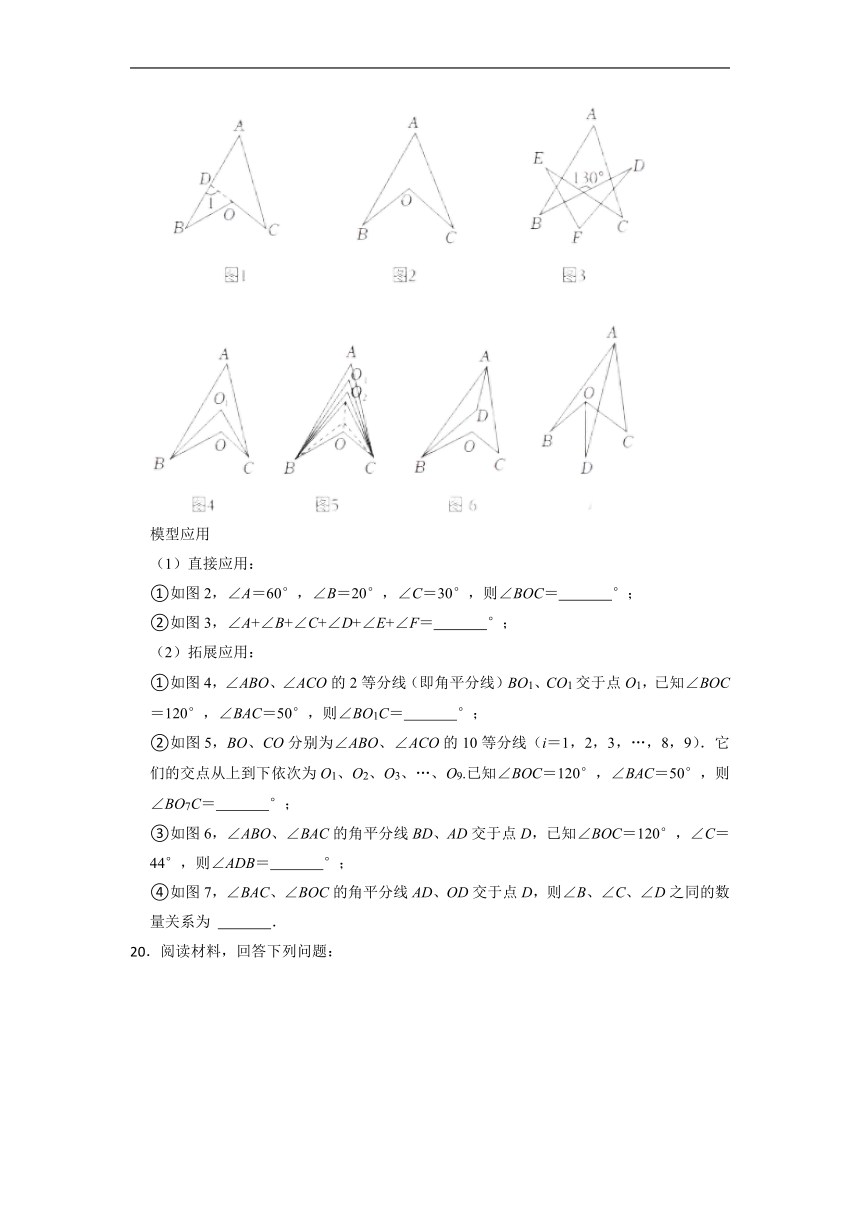
(1)直接应用:
①如图2,∠A=60°,∠B=20°,∠C=30°,则∠BOC= °;
②如图3,∠A+∠B+∠C+∠D+∠E+∠F= °;
(2)拓展应用:
①如图4,∠ABO、∠ACO的2等分线(即角平分线)BO1、CO1交于点O1,已知∠BOC=120°,∠BAC=50°,则∠BO1C= °;
②如图5,BO、CO分别为∠ABO、∠ACO的10等分线(i=1,2,3,…,8,9).它们的交点从上到下依次为O1、O2、O3、…、O9.已知∠BOC=120°,∠BAC=50°,则∠BO7C= °;
③如图6,∠ABO、∠BAC的角平分线BD、AD交于点D,已知∠BOC=120°,∠C=44°,则∠ADB= °;
④如图7,∠BAC、∠BOC的角平分线AD、OD交于点D,则∠B、∠C、∠D之同的数量关系为 .
.阅读材料,回答下列问题:
【材料提出】
“八字型”是数学几何的常用模型,通常由一组对顶角所在的两个三角形构成.
【探索研究】
探索一:如图1,在八字型中,探索∠A、∠B、∠C、∠D之间的数量关系为 ;
探索二:如图2,若∠B=36°,∠D=14°,求∠P的度数为 ;
探索三:如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,则∠P、∠B、∠D之间的数量关系为 .
【模型应用】
应用一:如图4,延长BM、CN,交于点A,在四边形MNCB中,设∠M=α,∠N=β,α+β>180°,四边形的内角∠MBC与外角∠NCD的角平分线BP,CP相交于点P,则∠A= (用含有α和β的代数式表示),∠P= .(用含有α和β的代数式表示)
应用二:如图5,在四边形MNCB中,设∠M=α,∠N=β,α+β<180°,四边形的内角∠MBC与外角∠NCD的角平分线所在的直线相交于点P,∠P= .(用含有α和β的代数式表示)
【拓展延伸】
拓展一:如图6,若设∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B之间的数量关系为 .(用x、y表示∠P)
拓展二:如图7,AP平分∠BAD,CP平分∠BCD的邻补角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论 .
参考答案与试题解析
一.选择题
.【解答】解:设这个多边形的边数为n(n为正整数且n≥3).
由题意得:1180°<180°(n﹣2)<1180°+180°.
∴1180°<180°(n﹣2)<1360°.
∴.
∴n=9.
∴这个多边形的内角和为180°×(9﹣2)=1260°.
∴少算的这个角的度数为1260°﹣1180°=80°.
故选:C.
.【解答】解:∵此多边形每个外角都等于36°,
∴该多边形的边数为=10.
∴从这个多边形的某个顶点能画的对角线的条数为10﹣3=7(条).
故选:A.
.【解答】解:如图,延长AB并交l2于点M.
∵五边形ABCDE是正五边形,
∴正五边形ABCDE的每个外角相等.
∴∠MBC==72°.
∵l1∥l2,
∴∠2=∠BMD.
∵∠1=∠BMD+∠MBC,
∴∠BMD=∠1﹣∠MBC.
∴∠1﹣∠2=∠MBC=72°.
故选:C.
.【解答】解:①射线AB和射线BA的端点不同,故不是同一条射线,故错误;
②各边相等,各角也相等的多边形叫做正多边形,故正确;
③连接两点的线段的长叫做两点间的距离,故错误;
④两点之间,线段最短,故正确.
故选:B.
.【解答】解:∵∠A=64°,∠BCD=136°,
∴∠ADC+∠ABC=360°﹣∠A﹣∠BCD=160°,故②正确;
∵∠AEB=180°﹣∠A﹣∠ABC=116°﹣∠ABC,∠AFD=180°﹣∠A﹣∠ADC=116°﹣∠ADC,
∴∠AEB+∠AFD=116°﹣∠ABC+116°﹣∠ADC=232°﹣(∠ADC+∠ABC)=72°,
∵EP平分∠AEB,FP平分∠AFD,
∴,,
∴,故④正确;
同理:∠PEB+∠PFC=36°,
如图,连接AP并延长至点G,
∠EPF=∠EPG+∠FPG=∠EAP+∠AEP+∠FAP+∠AFP=∠EAF+∠AEP+∠AFP=64°+36°=100°,故①正确;
∴∠PEB+∠PFC+∠EPF=36°+100°=136°,故③正确.
故选:D.
【解答】解:如图,过点D′作D′G∥AD,则∠2=∠ED′G,
∵AD∥BC,
∴BC∥D′G,
∴∠3=∠C′D′G,
∵AD∥BC,
∴∠1=∠4,
根据折叠的性质得:∠4=∠5,
∵∠1=2∠2,
∴∠4=∠5=2∠2,
∴2∠2+2∠2+∠2=180°,
∴∠2=36°,
∵∠ED′C′=∠D=90°,
∴∠2+∠3=90°,
∴∠3=90°﹣36°=54°,
故选:B.
【解答】解:∵72÷8=9,
∴360°÷9=40°.
∴每次旋转的角度α=40°.
故选:B.
【解答】解:∵六边形ABCDEF是正六边形,
∴正六边形的一个内角=×(6﹣2)×180°=120°,
∠ABC=∠FAB=120°,AB=BC,
∵四边形BCGH是正方形,
∴∠HBC=90°,BC=BH,
∴AB=BH,∠ABH=30°,
∴∠HAB=∠AHB=(180°﹣30°)÷2=75°,
∴∠FAH=∠FAB﹣∠HAB=120°﹣75°=45°,
故选:D.
【解答】解:由题意得,180°×(n﹣2)+360°=1800°,
解得:n=10,
故选:D.
【解答】解:如图,
由三角形外角性质可知:
∠1=∠F+∠B,∠2=∠A+∠E,
∴在四边形ADCG中,由四边形内角和可知:
∠D+∠C+∠2+∠1=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故选:C.
二.填空题
.【解答】解:∵一个多边形的每个外角都等于36°,
∴多边形的边数为360°÷36°=10.
即该多边形由10条边.
故答案是:10.
.【解答】解:设这个正多边形的边数为n,
∵一个正多边形的内角和为720°,
∴180(n﹣2)=720,
解得:n=6,
∴这个正多边形的每一个外角是:360°÷6=60°.
故答案为:60°.
.【解答】解:∵多边形的外角和为360°,
∴SA1+SA2+…+SAn=S圆=π×22=π(cm2).
故答案为4π.
.【解答】解:∵一个正多边形的每个内角都是144°,
∴它的每一个外角都是:180°﹣144°=36°,
∴它的边数为:360°÷36=10,
∴这个多边形的内角和为:180°(10﹣2)=1440°,
故答案为:1440°.
.【解答】解:易得此几何体为正多边形,每个外角为15°,
∴这个多边形的边数为360°÷15=24,
∴当他第一次回到点A时共走了24×10=240m.
三.解答题
.【解答】解:(1)∵a,b,c是△ABC的三边的长,
∴a+b>c,a+c>b,b+c>a,
∴a﹣b﹣c<0,b﹣c﹣a<0,c+a﹣b>0,
∴|a﹣b﹣c|+|b﹣c﹣a|+|c+a﹣b|=﹣a+b+c﹣b+c+a+c+a﹣b=3c+a﹣b.
(2)∵正多边形的内角与其外角的度数比为3:1
∴每一个外角为180°×=45°,
∴边数=360°÷45°=8,
即这个多边形的边数为8.
.【解答】解:(1)①∵OB,OC分别平分∠ABC,∠ACB,
∴∠OBC=∠ABC,∠OBC=∠ACB,
∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°
∴∠O=180°﹣∠OBC﹣∠OCB
=180°﹣∠ABC﹣∠ACB
=180°﹣(∠ABC+∠ACB)
=180°﹣65°
=115°;
同理得:∠P=180°﹣∠PBC﹣∠PCB
=180°﹣∠DBC﹣∠ECB
=180°﹣(∠DBC+∠ECB)
=180°﹣(180°﹣∠ABC+180°﹣∠ACB)
=180°﹣[360°﹣(∠ABC+∠ACB)]
=180°﹣(360°﹣130°)
=65°;
故答案为:115°;65°.
②∵∠A=α,
∴∠ABC+∠ACB=180°﹣α
∴∠O=180°﹣∠OBC﹣∠OCB
=180°﹣∠ABC﹣∠ACB
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣α)
=90°+α;
同理得:∠P=180°﹣[360°﹣(∠ABC+∠ACB)]
=180°﹣[360°﹣(180°﹣α)]
=90°﹣α;
故答案为:90°+α;90°﹣α;
(2)∠P=180°﹣(∠A+∠D).理由如下:
∵BP,CP分别平分外角∠EBC,∠FCB,
∴∠PBC=∠EBC,∠PCB=∠BCF,
∴∠P=180°﹣(∠PBC+∠PCB)
=180°﹣(∠EBC+∠FCB)
=180°﹣[360°﹣(∠ABC+∠DCB)]
=(∠ABC+∠DCB)
=(360°﹣∠A﹣∠D)
=180°﹣(∠A+∠D).
.【解答】解:(1)如图,
由三角形外角的性质可得,∠1=∠A3+∠A5,∠2=∠A2+∠A4,
∵∠1+∠2+∠A1=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=180°,
故答案为:180°;
(2)如图,
由三角形外角的性质可得,
∠8=∠A2+∠A6,∠10=∠A7+∠A4,∠11=∠A1+∠A5,∠9=∠A3+∠10=∠A3+∠A4+∠A7,
∵∠8+∠9+∠11=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7=180°;
(3)如图,
由三角形外角的性质可得,
∠9=∠A1+∠A4,∠10=∠A3+∠A8,∠11=∠A2+∠A7,∠12=∠11+∠A5=∠A2+∠A7+∠A5,
∵∠9+∠10+∠12+∠A6=360°,
∴∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8=360°,
故答案为:360°.
.【解答】解:(1)①∵∠BOC=∠A+∠B+∠C,
∴∠BOC=60°+30°+20°=110°,
故答案为:110;
②如图,
在四边形ABOC中,∠A+∠B+∠C=∠BOC=130°,
在四边形DOEF中,∠D+∠E+∠F=∠DOE=130°,
∴∠A+∠B+∠C+∠D+∠E+∠F=2×130°=260°,
故答案为:260;
(2)①如图,
∵∠BOC=∠ABO+∠ACO+∠A,∠BO1C=∠1+∠2+∠A,且∠ABO=2∠1,∠ACO=2∠2,
∴∠ABO+∠ACO=∠BOC﹣∠A=120°﹣50°=70°,
∴∠1+∠2=(∠ABO+∠ACO)=35°,
∴∠BO1C=∠1+∠2+∠A=35°+50°=85°,
故答案为:85;
②由题意知,∠ABO+∠ACO=∠BOC﹣∠BAC=120°﹣50°=70°,
∵∠OBO7=∠ABO,∠OCO7=∠ACO,
∴∠BO7C=120°﹣(∠OBO7+∠OCO7)=120°﹣(∠ABO+∠ACO)=120°﹣21°=99°,
故答案为:99;
③∵∠BOC=120°,∠C=44°,
∴∠ABO+∠BAC=120°﹣44°=76°,
∵∠ABO、∠BAC的角平分线BD、AD交于点D,
∴∠ABD+∠DAB=(∠ABO+∠BAC)=38°,
∴∠ADB=180°﹣(∠ABD+∠DAB)=180°﹣38°=142°,
故答案为:142;
④由“8字模型”可得,∠DOC+∠D=∠DAC+∠C,
∴∠D=∠DAC+∠C﹣∠DOC,
∵∠DOC=BOC=(∠BAC+∠B+∠C),∠DAC=BAC,
∴∠D=∠BAC+∠C﹣(∠BAC+∠B+∠C)=﹣B=(∠C﹣∠B),
故答案为:∠D=(∠C﹣∠B).
.【解答】解:探索一:如图1,∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为∠A+∠B=∠C+∠D;
探索二:如图2,∵AP、CP分别平分∠BAD、∠BCD,
∴∠1=∠2,∠3=∠4,
由(1)可得:∠1+∠B=∠3+∠P,∠2+∠P=∠4+∠D,
∴∠B﹣∠P=∠P﹣∠D,
即2∠P=∠B+∠D,
∵∠B=36°,∠D=14°,
∴∠P=25°,
故答案为25°;
探索三:由①∠D+2∠1=∠B+2∠3,
由②2∠B+2∠3=2∠P+2∠1,
①+②得:∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1
∠D+2∠B=2∠P+∠B.
∴∠P=.
故答案为:∠P=.
应用一:如图4,由题意知延长BM、CN,交于点A,
∵∠M=α,∠N=β,α+β>180°,
∴∠AMN=180°﹣α,∠ANM=180°﹣β,
∴∠A=180°﹣(∠AMN+∠ANM)=180°﹣(180°﹣α+180°﹣β)=α+β﹣180°;
∵BP、CP分别平分∠ABC、∠ACB,
∴∠PBC=∠ABC,∠PCD=∠ACD,
∵∠PCD=∠P+∠PBC,
∴∠P=∠PCD﹣∠PBC=(∠ACD﹣∠ABC)=∠A=,
故答案为:α+β﹣180°,;
应用二:如图5,延长MB、NC,交于点A,设T是CB的延长线上一点,R是BC延长线上一点,
∵∠M=α,∠N=β,α+β<180°,
∴∠A=180°﹣α﹣β,
∵BP平分∠MBC,CP平分∠NCR,
∴BP平分∠ABT,CP平分∠ACB,
由应用一得:∠P=∠A=,
故答案为:;
拓展一:如图6,由探索一可得:
∠P+∠PAB=∠B+∠PDB,∠P+∠CDP=∠C+∠CAP,∠B+∠CDB=∠C+∠CAB,
∵∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,
∴∠CDB﹣∠CAB=∠C﹣∠B=x﹣y,
∠PAB=∠CAB,∠PDB=∠CDB,
∴∠P+∠CAB=∠B+∠CDB,∠P+∠CDB=∠C+∠CAB,
∴2∠P=∠C+∠B+(∠CDB﹣∠CAB)=x+y+(x﹣y)=,
∴∠P=,
故答案为:∠P=;
拓展二:如图7,
∵AP平分∠BAD,CP平分∠BCD的邻补角∠BCE,
∴∠PAD=∠BAD,∠PCD=90°+∠BCD,
由探索一得:①∠B+∠BAD=∠D+∠BCD,②∠P+∠PAD=∠D+∠PCD,
②×2,得:③2∠P+∠BAD=2∠D+180°+∠BCD,
③﹣①,得:2∠P﹣∠B=∠D+180°,
∴2∠P﹣∠B﹣∠D=180°,
故答案为:2∠P﹣∠B﹣∠D=180°.
一.选择题
.在计算一个多边形的内角和时,由于粗心少算了1个内角,其和等于1180°,则少算的这个角的度数是( )
A.60° B.70° C.80° D.90°
.一个多边形每个外角都等于36°,则从这个多边形的某个顶点画对角线,最多可以画出几条( )
A.7条 B.8条 C.9条 D.10条
.如图,五边形ABCDE是正五边形,若l1∥l2,则∠1﹣∠2的值是( )
A.108° B.36° C.72° D.144°
.下列叙述正确的有( )个.
①射线AB的端点是A和B;
②各边相等,各角也相等的多边形叫做正多边形;
③连接两点的线段叫做两点的距离;
④两点之间线段最短.
A.1 B.2 C.3 D.4
.四边形ABCD两组对边AD,BC与AB,DC延长线分别交于点E,F,∠AEB,∠AFD的平分线交于点P,∠A=64°,∠BCD=136°,则下列结论中正确的是( )
①∠EPF=100°;②∠ADC+∠ABC=160°;③∠PEB+∠PFC+∠EPF=136°;④∠PEA+∠PFA=36°
A.①②③ B.②③④ C.①③④ D.①②③④
如图,四边形ABCD为一长方形纸带,AD∥BC,将四边形ABCD沿EF折叠,C、D两点分别与C′、D′对应,若∠1=2∠2,则∠3的度数为( )
A.50° B.54° C.58° D.62°
如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α,再沿直线前进8米,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度α为( )
A.30° B.40° C.45° D.60°
如图,在正六边形ABCDEF内作正方形BCGH,连接AH,则∠FAH等于( )
A.75° B.72° C.60° D.45°
若n边形的内角和与外角和相加为1800°,则n的值为( )
A.7 B.8. C.9 D.10
如图,∠A+∠B+∠C+∠D+∠E+∠F=( )
A.180° B.240° C.360° D.540°
二.填空题
.若一个多边形每一个外角都等于36°,则这个多边形有 条边.
.一个正多边形的内角和为720°,则这个正多边形的每一个外角等于 .
.如图所示,分别以n边形顶角顶点为圆心,以2cm长为半径画圆,则圆中阴影部分面积之和为 cm2.
.一个正多边形的每个内角都是144°,则这个多边形的内角和为 .
.如图,小华从点A出发向前走10m,向右转15°,然后继续向前走10m,再向右转15°,他以同样的方法继续走下去,当他第一次回到点A时共走了 m.
解答题
.化简/求解:
(1)若a,b,c是△ABC的三边的长,化简|a﹣b﹣c|+|b﹣c﹣a|+|c+a﹣b|.
(2)已知一正多边形的内角与其相邻的外角的比为3:1,求该多边形的边数.
.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB.
①若∠A=50°,则∠O= ,∠P= ;
②若∠A=α,则∠O= ,∠P= .(用含α的式子表示)
(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P与∠A,∠D的数量关系,并说明理由.
.利用“模型”解决几何综合问题往往会取得事半功倍的效果.
几何模型:如图(1),我们称它为“A”型图案,
易证明:∠EDF=∠A+∠B+∠C;
应用上面模型解决问题:
(1)如图(2),“五角星”形,求∠A1+∠A2+∠A3+∠A4+∠A5=?
分析:图中A1A3DA4是“A”型图,于是∠A2DA5=∠A1+∠A3+∠A4,
所以∠A1+∠A2+∠A3+∠A4+∠A5= ;
(2)如图(3),“七角星”形,求∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7;
(3)如图(4),“八角星”形,可以求得:∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8= ;
.模型规律:如图1,延长CO交AB于点D,则∠BOC=∠1+∠B=∠A+∠C+∠B.
因为凹四边形ABOC形似箭头,其四角具有“∠BOC=∠A+∠B+∠C”这个规律,所以我们把这个模型叫做“箭头四角形”.
模型应用
(1)直接应用:
①如图2,∠A=60°,∠B=20°,∠C=30°,则∠BOC= °;
②如图3,∠A+∠B+∠C+∠D+∠E+∠F= °;
(2)拓展应用:
①如图4,∠ABO、∠ACO的2等分线(即角平分线)BO1、CO1交于点O1,已知∠BOC=120°,∠BAC=50°,则∠BO1C= °;
②如图5,BO、CO分别为∠ABO、∠ACO的10等分线(i=1,2,3,…,8,9).它们的交点从上到下依次为O1、O2、O3、…、O9.已知∠BOC=120°,∠BAC=50°,则∠BO7C= °;
③如图6,∠ABO、∠BAC的角平分线BD、AD交于点D,已知∠BOC=120°,∠C=44°,则∠ADB= °;
④如图7,∠BAC、∠BOC的角平分线AD、OD交于点D,则∠B、∠C、∠D之同的数量关系为 .
.阅读材料,回答下列问题:
【材料提出】
“八字型”是数学几何的常用模型,通常由一组对顶角所在的两个三角形构成.
【探索研究】
探索一:如图1,在八字型中,探索∠A、∠B、∠C、∠D之间的数量关系为 ;
探索二:如图2,若∠B=36°,∠D=14°,求∠P的度数为 ;
探索三:如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,则∠P、∠B、∠D之间的数量关系为 .
【模型应用】
应用一:如图4,延长BM、CN,交于点A,在四边形MNCB中,设∠M=α,∠N=β,α+β>180°,四边形的内角∠MBC与外角∠NCD的角平分线BP,CP相交于点P,则∠A= (用含有α和β的代数式表示),∠P= .(用含有α和β的代数式表示)
应用二:如图5,在四边形MNCB中,设∠M=α,∠N=β,α+β<180°,四边形的内角∠MBC与外角∠NCD的角平分线所在的直线相交于点P,∠P= .(用含有α和β的代数式表示)
【拓展延伸】
拓展一:如图6,若设∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B之间的数量关系为 .(用x、y表示∠P)
拓展二:如图7,AP平分∠BAD,CP平分∠BCD的邻补角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论 .
参考答案与试题解析
一.选择题
.【解答】解:设这个多边形的边数为n(n为正整数且n≥3).
由题意得:1180°<180°(n﹣2)<1180°+180°.
∴1180°<180°(n﹣2)<1360°.
∴.
∴n=9.
∴这个多边形的内角和为180°×(9﹣2)=1260°.
∴少算的这个角的度数为1260°﹣1180°=80°.
故选:C.
.【解答】解:∵此多边形每个外角都等于36°,
∴该多边形的边数为=10.
∴从这个多边形的某个顶点能画的对角线的条数为10﹣3=7(条).
故选:A.
.【解答】解:如图,延长AB并交l2于点M.
∵五边形ABCDE是正五边形,
∴正五边形ABCDE的每个外角相等.
∴∠MBC==72°.
∵l1∥l2,
∴∠2=∠BMD.
∵∠1=∠BMD+∠MBC,
∴∠BMD=∠1﹣∠MBC.
∴∠1﹣∠2=∠MBC=72°.
故选:C.
.【解答】解:①射线AB和射线BA的端点不同,故不是同一条射线,故错误;
②各边相等,各角也相等的多边形叫做正多边形,故正确;
③连接两点的线段的长叫做两点间的距离,故错误;
④两点之间,线段最短,故正确.
故选:B.
.【解答】解:∵∠A=64°,∠BCD=136°,
∴∠ADC+∠ABC=360°﹣∠A﹣∠BCD=160°,故②正确;
∵∠AEB=180°﹣∠A﹣∠ABC=116°﹣∠ABC,∠AFD=180°﹣∠A﹣∠ADC=116°﹣∠ADC,
∴∠AEB+∠AFD=116°﹣∠ABC+116°﹣∠ADC=232°﹣(∠ADC+∠ABC)=72°,
∵EP平分∠AEB,FP平分∠AFD,
∴,,
∴,故④正确;
同理:∠PEB+∠PFC=36°,
如图,连接AP并延长至点G,
∠EPF=∠EPG+∠FPG=∠EAP+∠AEP+∠FAP+∠AFP=∠EAF+∠AEP+∠AFP=64°+36°=100°,故①正确;
∴∠PEB+∠PFC+∠EPF=36°+100°=136°,故③正确.
故选:D.
【解答】解:如图,过点D′作D′G∥AD,则∠2=∠ED′G,
∵AD∥BC,
∴BC∥D′G,
∴∠3=∠C′D′G,
∵AD∥BC,
∴∠1=∠4,
根据折叠的性质得:∠4=∠5,
∵∠1=2∠2,
∴∠4=∠5=2∠2,
∴2∠2+2∠2+∠2=180°,
∴∠2=36°,
∵∠ED′C′=∠D=90°,
∴∠2+∠3=90°,
∴∠3=90°﹣36°=54°,
故选:B.
【解答】解:∵72÷8=9,
∴360°÷9=40°.
∴每次旋转的角度α=40°.
故选:B.
【解答】解:∵六边形ABCDEF是正六边形,
∴正六边形的一个内角=×(6﹣2)×180°=120°,
∠ABC=∠FAB=120°,AB=BC,
∵四边形BCGH是正方形,
∴∠HBC=90°,BC=BH,
∴AB=BH,∠ABH=30°,
∴∠HAB=∠AHB=(180°﹣30°)÷2=75°,
∴∠FAH=∠FAB﹣∠HAB=120°﹣75°=45°,
故选:D.
【解答】解:由题意得,180°×(n﹣2)+360°=1800°,
解得:n=10,
故选:D.
【解答】解:如图,
由三角形外角性质可知:
∠1=∠F+∠B,∠2=∠A+∠E,
∴在四边形ADCG中,由四边形内角和可知:
∠D+∠C+∠2+∠1=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故选:C.
二.填空题
.【解答】解:∵一个多边形的每个外角都等于36°,
∴多边形的边数为360°÷36°=10.
即该多边形由10条边.
故答案是:10.
.【解答】解:设这个正多边形的边数为n,
∵一个正多边形的内角和为720°,
∴180(n﹣2)=720,
解得:n=6,
∴这个正多边形的每一个外角是:360°÷6=60°.
故答案为:60°.
.【解答】解:∵多边形的外角和为360°,
∴SA1+SA2+…+SAn=S圆=π×22=π(cm2).
故答案为4π.
.【解答】解:∵一个正多边形的每个内角都是144°,
∴它的每一个外角都是:180°﹣144°=36°,
∴它的边数为:360°÷36=10,
∴这个多边形的内角和为:180°(10﹣2)=1440°,
故答案为:1440°.
.【解答】解:易得此几何体为正多边形,每个外角为15°,
∴这个多边形的边数为360°÷15=24,
∴当他第一次回到点A时共走了24×10=240m.
三.解答题
.【解答】解:(1)∵a,b,c是△ABC的三边的长,
∴a+b>c,a+c>b,b+c>a,
∴a﹣b﹣c<0,b﹣c﹣a<0,c+a﹣b>0,
∴|a﹣b﹣c|+|b﹣c﹣a|+|c+a﹣b|=﹣a+b+c﹣b+c+a+c+a﹣b=3c+a﹣b.
(2)∵正多边形的内角与其外角的度数比为3:1
∴每一个外角为180°×=45°,
∴边数=360°÷45°=8,
即这个多边形的边数为8.
.【解答】解:(1)①∵OB,OC分别平分∠ABC,∠ACB,
∴∠OBC=∠ABC,∠OBC=∠ACB,
∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°
∴∠O=180°﹣∠OBC﹣∠OCB
=180°﹣∠ABC﹣∠ACB
=180°﹣(∠ABC+∠ACB)
=180°﹣65°
=115°;
同理得:∠P=180°﹣∠PBC﹣∠PCB
=180°﹣∠DBC﹣∠ECB
=180°﹣(∠DBC+∠ECB)
=180°﹣(180°﹣∠ABC+180°﹣∠ACB)
=180°﹣[360°﹣(∠ABC+∠ACB)]
=180°﹣(360°﹣130°)
=65°;
故答案为:115°;65°.
②∵∠A=α,
∴∠ABC+∠ACB=180°﹣α
∴∠O=180°﹣∠OBC﹣∠OCB
=180°﹣∠ABC﹣∠ACB
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣α)
=90°+α;
同理得:∠P=180°﹣[360°﹣(∠ABC+∠ACB)]
=180°﹣[360°﹣(180°﹣α)]
=90°﹣α;
故答案为:90°+α;90°﹣α;
(2)∠P=180°﹣(∠A+∠D).理由如下:
∵BP,CP分别平分外角∠EBC,∠FCB,
∴∠PBC=∠EBC,∠PCB=∠BCF,
∴∠P=180°﹣(∠PBC+∠PCB)
=180°﹣(∠EBC+∠FCB)
=180°﹣[360°﹣(∠ABC+∠DCB)]
=(∠ABC+∠DCB)
=(360°﹣∠A﹣∠D)
=180°﹣(∠A+∠D).
.【解答】解:(1)如图,
由三角形外角的性质可得,∠1=∠A3+∠A5,∠2=∠A2+∠A4,
∵∠1+∠2+∠A1=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=180°,
故答案为:180°;
(2)如图,
由三角形外角的性质可得,
∠8=∠A2+∠A6,∠10=∠A7+∠A4,∠11=∠A1+∠A5,∠9=∠A3+∠10=∠A3+∠A4+∠A7,
∵∠8+∠9+∠11=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7=180°;
(3)如图,
由三角形外角的性质可得,
∠9=∠A1+∠A4,∠10=∠A3+∠A8,∠11=∠A2+∠A7,∠12=∠11+∠A5=∠A2+∠A7+∠A5,
∵∠9+∠10+∠12+∠A6=360°,
∴∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8=360°,
故答案为:360°.
.【解答】解:(1)①∵∠BOC=∠A+∠B+∠C,
∴∠BOC=60°+30°+20°=110°,
故答案为:110;
②如图,
在四边形ABOC中,∠A+∠B+∠C=∠BOC=130°,
在四边形DOEF中,∠D+∠E+∠F=∠DOE=130°,
∴∠A+∠B+∠C+∠D+∠E+∠F=2×130°=260°,
故答案为:260;
(2)①如图,
∵∠BOC=∠ABO+∠ACO+∠A,∠BO1C=∠1+∠2+∠A,且∠ABO=2∠1,∠ACO=2∠2,
∴∠ABO+∠ACO=∠BOC﹣∠A=120°﹣50°=70°,
∴∠1+∠2=(∠ABO+∠ACO)=35°,
∴∠BO1C=∠1+∠2+∠A=35°+50°=85°,
故答案为:85;
②由题意知,∠ABO+∠ACO=∠BOC﹣∠BAC=120°﹣50°=70°,
∵∠OBO7=∠ABO,∠OCO7=∠ACO,
∴∠BO7C=120°﹣(∠OBO7+∠OCO7)=120°﹣(∠ABO+∠ACO)=120°﹣21°=99°,
故答案为:99;
③∵∠BOC=120°,∠C=44°,
∴∠ABO+∠BAC=120°﹣44°=76°,
∵∠ABO、∠BAC的角平分线BD、AD交于点D,
∴∠ABD+∠DAB=(∠ABO+∠BAC)=38°,
∴∠ADB=180°﹣(∠ABD+∠DAB)=180°﹣38°=142°,
故答案为:142;
④由“8字模型”可得,∠DOC+∠D=∠DAC+∠C,
∴∠D=∠DAC+∠C﹣∠DOC,
∵∠DOC=BOC=(∠BAC+∠B+∠C),∠DAC=BAC,
∴∠D=∠BAC+∠C﹣(∠BAC+∠B+∠C)=﹣B=(∠C﹣∠B),
故答案为:∠D=(∠C﹣∠B).
.【解答】解:探索一:如图1,∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为∠A+∠B=∠C+∠D;
探索二:如图2,∵AP、CP分别平分∠BAD、∠BCD,
∴∠1=∠2,∠3=∠4,
由(1)可得:∠1+∠B=∠3+∠P,∠2+∠P=∠4+∠D,
∴∠B﹣∠P=∠P﹣∠D,
即2∠P=∠B+∠D,
∵∠B=36°,∠D=14°,
∴∠P=25°,
故答案为25°;
探索三:由①∠D+2∠1=∠B+2∠3,
由②2∠B+2∠3=2∠P+2∠1,
①+②得:∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1
∠D+2∠B=2∠P+∠B.
∴∠P=.
故答案为:∠P=.
应用一:如图4,由题意知延长BM、CN,交于点A,
∵∠M=α,∠N=β,α+β>180°,
∴∠AMN=180°﹣α,∠ANM=180°﹣β,
∴∠A=180°﹣(∠AMN+∠ANM)=180°﹣(180°﹣α+180°﹣β)=α+β﹣180°;
∵BP、CP分别平分∠ABC、∠ACB,
∴∠PBC=∠ABC,∠PCD=∠ACD,
∵∠PCD=∠P+∠PBC,
∴∠P=∠PCD﹣∠PBC=(∠ACD﹣∠ABC)=∠A=,
故答案为:α+β﹣180°,;
应用二:如图5,延长MB、NC,交于点A,设T是CB的延长线上一点,R是BC延长线上一点,
∵∠M=α,∠N=β,α+β<180°,
∴∠A=180°﹣α﹣β,
∵BP平分∠MBC,CP平分∠NCR,
∴BP平分∠ABT,CP平分∠ACB,
由应用一得:∠P=∠A=,
故答案为:;
拓展一:如图6,由探索一可得:
∠P+∠PAB=∠B+∠PDB,∠P+∠CDP=∠C+∠CAP,∠B+∠CDB=∠C+∠CAB,
∵∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,
∴∠CDB﹣∠CAB=∠C﹣∠B=x﹣y,
∠PAB=∠CAB,∠PDB=∠CDB,
∴∠P+∠CAB=∠B+∠CDB,∠P+∠CDB=∠C+∠CAB,
∴2∠P=∠C+∠B+(∠CDB﹣∠CAB)=x+y+(x﹣y)=,
∴∠P=,
故答案为:∠P=;
拓展二:如图7,
∵AP平分∠BAD,CP平分∠BCD的邻补角∠BCE,
∴∠PAD=∠BAD,∠PCD=90°+∠BCD,
由探索一得:①∠B+∠BAD=∠D+∠BCD,②∠P+∠PAD=∠D+∠PCD,
②×2,得:③2∠P+∠BAD=2∠D+180°+∠BCD,
③﹣①,得:2∠P﹣∠B=∠D+180°,
∴2∠P﹣∠B﹣∠D=180°,
故答案为:2∠P﹣∠B﹣∠D=180°.
