1.2 位置变化的描述-位移(含解析)
文档属性
| 名称 | 1.2 位置变化的描述-位移(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-10-05 11:01:19 | ||
图片预览



文档简介
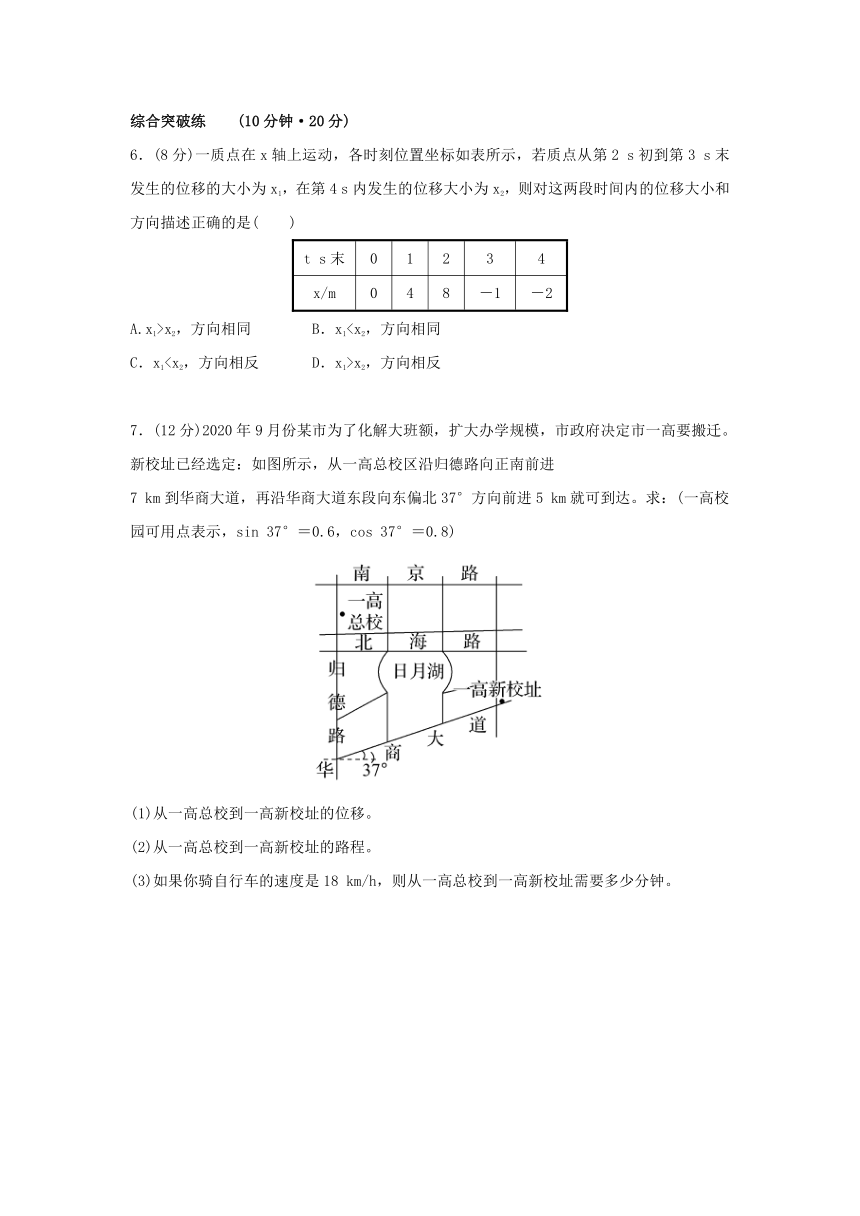
位置变化的描述——位移
基础全面练 (15分钟·30分)
一、选择题(本题共4小题,每题5分,共20分)
1.(2021·鹤壁高一检测)某人向正东方向运动了x米,然后再沿东偏北60°方向又运动了x米,则该人运动的位移大小为( )
A.x米 B.x米 C.x米 D.2x米
【变式训练】一个物体从A点运动到B点,下列结论正确的是( )
A.物体的位移一定等于路程
B.物体的位移与路程的方向相同,都从A指向B
C.物体位移的大小总是小于或等于它的路程
D.物体的位移是直线,而路程是曲线
2.如图所示,物体沿边长为a的正方形由A点如箭头所示的路径运动到D点,则它的位移和路程分别是( )
A.3a,方向向上;3a B.a,方向向下;3a
C.a,方向向上;3a D.a,方向向下;3a,方向向下
3.下列各组物理量中,全部是矢量的是( )
A.位移、时间、速度
B.质量、路程、速度、平均速度
C.速度、平均速度、位移
D.位移、路程、时间
4.小明沿半径为50 m的圆形草坪边缘绕跑一圈后回到起点,在跑步过程中,小明的路程和位移大小的最大值分别是( )
A.100π m,100 m B.100 m,0
C.50 m,50 m D.50 m,0
二、计算题(10分。要有必要的文字说明和解题步骤,有数值计算的要注明单位)
5.李敏从O点出发,沿东偏北30°的方向运动10 m至A点,然后又向正南方向运动5 m至B点。
(1)建立适当的坐标系,描述出李敏的运动轨迹。
(2)依据建立的坐标系,分别求出A、B两点的坐标。
【变式训练】某测绘规划技术人员在一次对某学校进行测量时,他从操场上某点A处开始,先向南走了30 m到达B处,再向东走了40 m到达C处,最后又向北走了60 m到达D处,则:
(1)这人步行的总路程和位移的大小各是多少?
(2)要比较确切地表示此人的位置变化,应该用位移还是路程?
综合突破练 (10分钟·20分)
6.(8分)一质点在x轴上运动,各时刻位置坐标如表所示,若质点从第2 s初到第3 s末发生的位移的大小为x1,在第4 s内发生的位移大小为x2,则对这两段时间内的位移大小和方向描述正确的是( )
t s末 0 1 2 3 4
x/m 0 4 8 -1 -2
A.x1>x2,方向相同 B.x1C.x1x2,方向相反
7.(12分)2020年9月份某市为了化解大班额,扩大办学规模,市政府决定市一高要搬迁。新校址已经选定:如图所示,从一高总校区沿归德路向正南前进
7 km到华商大道,再沿华商大道东段向东偏北37°方向前进5 km就可到达。求:(一高校园可用点表示,sin 37°=0.6,cos 37°=0.8)
(1)从一高总校到一高新校址的位移。
(2)从一高总校到一高新校址的路程。
(3)如果你骑自行车的速度是18 km/h,则从一高总校到一高新校址需要多少分钟。
参考答案:
基础全面练 (15分钟·30分)
一、选择题(本题共4小题,每题5分,共20分)
1.(2021·鹤壁高一检测)某人向正东方向运动了x米,然后再沿东偏北60°方向又运动了x米,则该人运动的位移大小为( )
A.x米 B.x米 C.x米 D.2x米
【解析】选C。作出图像,三点之间正好组成了一个知两边与一角的三角形,x1=x·cos60°=,x2=xsin60°=x,l2=(x1+x)2+x,l=x该人运动的位移大小为x米。故选C。
【变式训练】一个物体从A点运动到B点,下列结论正确的是( )
A.物体的位移一定等于路程
B.物体的位移与路程的方向相同,都从A指向B
C.物体位移的大小总是小于或等于它的路程
D.物体的位移是直线,而路程是曲线
【解析】选C。位移是矢量,路程是标量,故A、B错误;物体做单向直线运动时,位移的大小等于路程,做其他类型的运动时,位移的大小小于路程,故C正确;位移和路程都是描述物体运动的物理量,位移与初、末位置有关,路程与运动轨迹有关,不一定是曲线,故D错误。
2.如图所示,物体沿边长为a的正方形由A点如箭头所示的路径运动到D点,则它的位移和路程分别是( )
A.3a,方向向上;3a B.a,方向向下;3a
C.a,方向向上;3a D.a,方向向下;3a,方向向下
【解析】选C。路程等于运动轨迹的长度,从A到D,路程s=3a,位移的大小等于AD间的距离,即位移为a,方向向上,故C项正确。
3.下列各组物理量中,全部是矢量的是( )
A.位移、时间、速度
B.质量、路程、速度、平均速度
C.速度、平均速度、位移
D.位移、路程、时间
【解析】选C。 位移、时间、速度,其中时间不是矢量,故A错误; 质量、路程、速度、平均速度,其中质量和路程不是矢量,故B错误; 速度、平均速度、位移,三个都是矢量,故C正确; 位移、路程、时间,其中时间和路程不是矢量,故D错误。
4.小明沿半径为50 m的圆形草坪边缘绕跑一圈后回到起点,在跑步过程中,小明的路程和位移大小的最大值分别是( )
A.100π m,100 m B.100 m,0
C.50 m,50 m D.50 m,0
【解析】选A。小明沿半径为50 m的圆形草坪边缘绕跑一圈后回到起点,根据路程概念,最长的路程应该是圆形草坪的周长,即l=2πR=100π m,当小明跑半圈时位移最大,最大为圆形草坪的直径100 m。故A项正确。
二、计算题(10分。要有必要的文字说明和解题步骤,有数值计算的要注明单位)
5.李敏从O点出发,沿东偏北30°的方向运动10 m至A点,然后又向正南方向运动5 m至B点。
(1)建立适当的坐标系,描述出李敏的运动轨迹。
(2)依据建立的坐标系,分别求出A、B两点的坐标。
【解析】(1)李敏的运动轨迹是在同一个平面内,故需要建立平面直角坐标系。以O点为原点,以正东方向为x轴正方向,正北方向为y轴正方向,建立如图所示的坐标系,OAB为李敏的运动轨迹。
(2)A点到O点的距离为10 m,则可得
A点坐标:xA=OA×cos30°=5 m,yA=OA×sin30°=5 m。
B点坐标:xB=5 m,因为李敏由A点向正南方向运动5 m,与A点到x轴的距离相等,所以yB=0。
故A点的坐标为(5 m,5 m),B点的坐标为(5 m,0 )。
答案:(1)见解析 (2)A(5 m,5 m) B(5 m,0 )
【变式训练】某测绘规划技术人员在一次对某学校进行测量时,他从操场上某点A处开始,先向南走了30 m到达B处,再向东走了40 m到达C处,最后又向北走了60 m到达D处,则:
(1)这人步行的总路程和位移的大小各是多少?
(2)要比较确切地表示此人的位置变化,应该用位移还是路程?
【解析】(1)如图,三角形AED为直角三角形,AE=40 m,DE=30 m,所以AD==50 m,A、D分别为起点和终点,所以位移的大小是50 m。
他走过的路程为:
30 m+40 m+60 m=130 m。
(2)为了确切描述此人的位置变化,应该用位移,这样既能表示他相对出发点的距离,又能表示他相对出发点的方向。
答案:(1)130 m 50 m (2)位移
综合突破练 (10分钟·20分)
6.(8分)一质点在x轴上运动,各时刻位置坐标如表所示,若质点从第2 s初到第3 s末发生的位移的大小为x1,在第4 s内发生的位移大小为x2,则对这两段时间内的位移大小和方向描述正确的是( )
t s末 0 1 2 3 4
x/m 0 4 8 -1 -2
A.x1>x2,方向相同 B.x1C.x1x2,方向相反
【解析】选A。由位移等于位置坐标变化可知,从第2秒初(第1秒末)到第3秒末发生位移为:-1 m-4 m=-5 m,第4 s内位移为:-2 m-(-1 m)=-1 m,两段时间内的位移大小分别为5 m和1 m,则x1>x2,负号表示方向,两段时间内的位移均为负方向。故A项正确。
7.(12分)2020年9月份某市为了化解大班额,扩大办学规模,市政府决定市一高要搬迁。新校址已经选定:如图所示,从一高总校区沿归德路向正南前进
7 km到华商大道,再沿华商大道东段向东偏北37°方向前进5 km就可到达。求:(一高校园可用点表示,sin 37°=0.6,cos 37°=0.8)
(1)从一高总校到一高新校址的位移。
(2)从一高总校到一高新校址的路程。
(3)如果你骑自行车的速度是18 km/h,则从一高总校到一高新校址需要多少分钟。
【解析】(1)向正南位移x1=s1-s2sin 37°=4 km,向正东位移x2=s2cos 37°=
4 km,故从一高总校到一高新校址的位移为x= eq \r(x+x) =4 km,由于tan θ==1,则θ=45°,即方向南偏东45°。
(2)从一高总校到一高新校址的路程为s=s1+s2=12 km。
(3)从一高总校到一高新校址所需的时间为t== h=40 min。
答案:(1)4 km,方向南偏东45° (2)12 km (3)40 min
PAGE
基础全面练 (15分钟·30分)
一、选择题(本题共4小题,每题5分,共20分)
1.(2021·鹤壁高一检测)某人向正东方向运动了x米,然后再沿东偏北60°方向又运动了x米,则该人运动的位移大小为( )
A.x米 B.x米 C.x米 D.2x米
【变式训练】一个物体从A点运动到B点,下列结论正确的是( )
A.物体的位移一定等于路程
B.物体的位移与路程的方向相同,都从A指向B
C.物体位移的大小总是小于或等于它的路程
D.物体的位移是直线,而路程是曲线
2.如图所示,物体沿边长为a的正方形由A点如箭头所示的路径运动到D点,则它的位移和路程分别是( )
A.3a,方向向上;3a B.a,方向向下;3a
C.a,方向向上;3a D.a,方向向下;3a,方向向下
3.下列各组物理量中,全部是矢量的是( )
A.位移、时间、速度
B.质量、路程、速度、平均速度
C.速度、平均速度、位移
D.位移、路程、时间
4.小明沿半径为50 m的圆形草坪边缘绕跑一圈后回到起点,在跑步过程中,小明的路程和位移大小的最大值分别是( )
A.100π m,100 m B.100 m,0
C.50 m,50 m D.50 m,0
二、计算题(10分。要有必要的文字说明和解题步骤,有数值计算的要注明单位)
5.李敏从O点出发,沿东偏北30°的方向运动10 m至A点,然后又向正南方向运动5 m至B点。
(1)建立适当的坐标系,描述出李敏的运动轨迹。
(2)依据建立的坐标系,分别求出A、B两点的坐标。
【变式训练】某测绘规划技术人员在一次对某学校进行测量时,他从操场上某点A处开始,先向南走了30 m到达B处,再向东走了40 m到达C处,最后又向北走了60 m到达D处,则:
(1)这人步行的总路程和位移的大小各是多少?
(2)要比较确切地表示此人的位置变化,应该用位移还是路程?
综合突破练 (10分钟·20分)
6.(8分)一质点在x轴上运动,各时刻位置坐标如表所示,若质点从第2 s初到第3 s末发生的位移的大小为x1,在第4 s内发生的位移大小为x2,则对这两段时间内的位移大小和方向描述正确的是( )
t s末 0 1 2 3 4
x/m 0 4 8 -1 -2
A.x1>x2,方向相同 B.x1
7.(12分)2020年9月份某市为了化解大班额,扩大办学规模,市政府决定市一高要搬迁。新校址已经选定:如图所示,从一高总校区沿归德路向正南前进
7 km到华商大道,再沿华商大道东段向东偏北37°方向前进5 km就可到达。求:(一高校园可用点表示,sin 37°=0.6,cos 37°=0.8)
(1)从一高总校到一高新校址的位移。
(2)从一高总校到一高新校址的路程。
(3)如果你骑自行车的速度是18 km/h,则从一高总校到一高新校址需要多少分钟。
参考答案:
基础全面练 (15分钟·30分)
一、选择题(本题共4小题,每题5分,共20分)
1.(2021·鹤壁高一检测)某人向正东方向运动了x米,然后再沿东偏北60°方向又运动了x米,则该人运动的位移大小为( )
A.x米 B.x米 C.x米 D.2x米
【解析】选C。作出图像,三点之间正好组成了一个知两边与一角的三角形,x1=x·cos60°=,x2=xsin60°=x,l2=(x1+x)2+x,l=x该人运动的位移大小为x米。故选C。
【变式训练】一个物体从A点运动到B点,下列结论正确的是( )
A.物体的位移一定等于路程
B.物体的位移与路程的方向相同,都从A指向B
C.物体位移的大小总是小于或等于它的路程
D.物体的位移是直线,而路程是曲线
【解析】选C。位移是矢量,路程是标量,故A、B错误;物体做单向直线运动时,位移的大小等于路程,做其他类型的运动时,位移的大小小于路程,故C正确;位移和路程都是描述物体运动的物理量,位移与初、末位置有关,路程与运动轨迹有关,不一定是曲线,故D错误。
2.如图所示,物体沿边长为a的正方形由A点如箭头所示的路径运动到D点,则它的位移和路程分别是( )
A.3a,方向向上;3a B.a,方向向下;3a
C.a,方向向上;3a D.a,方向向下;3a,方向向下
【解析】选C。路程等于运动轨迹的长度,从A到D,路程s=3a,位移的大小等于AD间的距离,即位移为a,方向向上,故C项正确。
3.下列各组物理量中,全部是矢量的是( )
A.位移、时间、速度
B.质量、路程、速度、平均速度
C.速度、平均速度、位移
D.位移、路程、时间
【解析】选C。 位移、时间、速度,其中时间不是矢量,故A错误; 质量、路程、速度、平均速度,其中质量和路程不是矢量,故B错误; 速度、平均速度、位移,三个都是矢量,故C正确; 位移、路程、时间,其中时间和路程不是矢量,故D错误。
4.小明沿半径为50 m的圆形草坪边缘绕跑一圈后回到起点,在跑步过程中,小明的路程和位移大小的最大值分别是( )
A.100π m,100 m B.100 m,0
C.50 m,50 m D.50 m,0
【解析】选A。小明沿半径为50 m的圆形草坪边缘绕跑一圈后回到起点,根据路程概念,最长的路程应该是圆形草坪的周长,即l=2πR=100π m,当小明跑半圈时位移最大,最大为圆形草坪的直径100 m。故A项正确。
二、计算题(10分。要有必要的文字说明和解题步骤,有数值计算的要注明单位)
5.李敏从O点出发,沿东偏北30°的方向运动10 m至A点,然后又向正南方向运动5 m至B点。
(1)建立适当的坐标系,描述出李敏的运动轨迹。
(2)依据建立的坐标系,分别求出A、B两点的坐标。
【解析】(1)李敏的运动轨迹是在同一个平面内,故需要建立平面直角坐标系。以O点为原点,以正东方向为x轴正方向,正北方向为y轴正方向,建立如图所示的坐标系,OAB为李敏的运动轨迹。
(2)A点到O点的距离为10 m,则可得
A点坐标:xA=OA×cos30°=5 m,yA=OA×sin30°=5 m。
B点坐标:xB=5 m,因为李敏由A点向正南方向运动5 m,与A点到x轴的距离相等,所以yB=0。
故A点的坐标为(5 m,5 m),B点的坐标为(5 m,0 )。
答案:(1)见解析 (2)A(5 m,5 m) B(5 m,0 )
【变式训练】某测绘规划技术人员在一次对某学校进行测量时,他从操场上某点A处开始,先向南走了30 m到达B处,再向东走了40 m到达C处,最后又向北走了60 m到达D处,则:
(1)这人步行的总路程和位移的大小各是多少?
(2)要比较确切地表示此人的位置变化,应该用位移还是路程?
【解析】(1)如图,三角形AED为直角三角形,AE=40 m,DE=30 m,所以AD==50 m,A、D分别为起点和终点,所以位移的大小是50 m。
他走过的路程为:
30 m+40 m+60 m=130 m。
(2)为了确切描述此人的位置变化,应该用位移,这样既能表示他相对出发点的距离,又能表示他相对出发点的方向。
答案:(1)130 m 50 m (2)位移
综合突破练 (10分钟·20分)
6.(8分)一质点在x轴上运动,各时刻位置坐标如表所示,若质点从第2 s初到第3 s末发生的位移的大小为x1,在第4 s内发生的位移大小为x2,则对这两段时间内的位移大小和方向描述正确的是( )
t s末 0 1 2 3 4
x/m 0 4 8 -1 -2
A.x1>x2,方向相同 B.x1
【解析】选A。由位移等于位置坐标变化可知,从第2秒初(第1秒末)到第3秒末发生位移为:-1 m-4 m=-5 m,第4 s内位移为:-2 m-(-1 m)=-1 m,两段时间内的位移大小分别为5 m和1 m,则x1>x2,负号表示方向,两段时间内的位移均为负方向。故A项正确。
7.(12分)2020年9月份某市为了化解大班额,扩大办学规模,市政府决定市一高要搬迁。新校址已经选定:如图所示,从一高总校区沿归德路向正南前进
7 km到华商大道,再沿华商大道东段向东偏北37°方向前进5 km就可到达。求:(一高校园可用点表示,sin 37°=0.6,cos 37°=0.8)
(1)从一高总校到一高新校址的位移。
(2)从一高总校到一高新校址的路程。
(3)如果你骑自行车的速度是18 km/h,则从一高总校到一高新校址需要多少分钟。
【解析】(1)向正南位移x1=s1-s2sin 37°=4 km,向正东位移x2=s2cos 37°=
4 km,故从一高总校到一高新校址的位移为x= eq \r(x+x) =4 km,由于tan θ==1,则θ=45°,即方向南偏东45°。
(2)从一高总校到一高新校址的路程为s=s1+s2=12 km。
(3)从一高总校到一高新校址所需的时间为t== h=40 min。
答案:(1)4 km,方向南偏东45° (2)12 km (3)40 min
PAGE
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
