高中数学人教A版必修第一册课件1.4.2 充要条件 (课件共33张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课件1.4.2 充要条件 (课件共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 11:06:00 | ||
图片预览










文档简介
(共33张PPT)
1.2命题及其关系、充分条件与必要条件
第2课时
考点一 命题及其关系
解析①的否定是“ x∈R,x2-x+1>0”中是真命题,①正确;
②的否命题是“若x2+x-6<0,则x≤2”,
由x2+x-6<0,得-3③由x2-5x+6=0,得x=2或x=3,原命题是假命题,
因此可知逆否命题为假命题,③错误.
综上可知,真命题是①,②.
答案 (2)C
原命题与逆否命题同真同假,逆命题与否命题同真同假
补充例题1
考点一 命题及其相互关系
考点一 命题及其相互关系
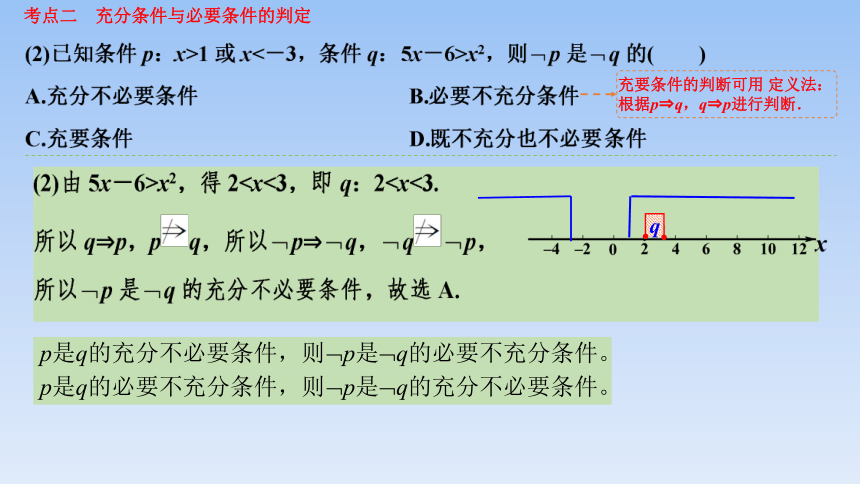
考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
即ab≤4,充分性成立;
当a=4,b=1时,满足ab≤4,
但a+b=5>4,不满足a+b≤4,
必要性不成立,
故“a+b≤4”是“ab≤4”的充分不必要条件.
答案 (1)A
考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
q
考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
解析 (2) (1)若m α,n α,m∥n,
由线面平行的判定定理知m∥α.
若m∥α,m α,n α,
不一定推出m∥n,直线m与n可能异面,
故“m∥n”是“m∥α”的充分不必要条件.
答案 (2)A
补充例题2
考点二 充分条件与必要条件的判定
考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
解析 (1)由“x2-5x<0”可得“0由“|x-1|<1”可得“0但0所以“x2-5x<0”是“|x-1|<1”的必要不充分条件.
答案 (1)B
由0考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
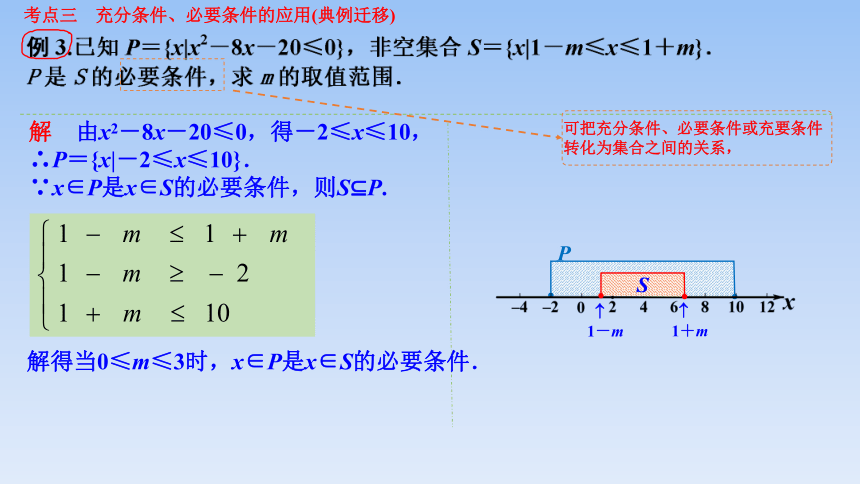
考点三 充分条件、必要条件的应用(典例迁移)
解 由x2-8x-20≤0,得-2≤x≤10,
∴P={x|-2≤x≤10}.
∵x∈P是x∈S的必要条件,则S P.
解得当0≤m≤3时,x∈P是x∈S的必要条件.
可把充分条件、必要条件或充要条件转化为集合之间的关系,
P
S
1-m
1+m
考点三 充分条件、必要条件的应用(典例迁移)
解 由例题知P={x|-2≤x≤10}.
∵¬P是¬S的必要不充分条件,
∴P是S的充分不必要条件,
∴ m≥9,则m的取值范围是[9,+∞).
可把充分条件、必要条件或充要条件转化为集合之间的关系,
S
1-m
1+m
P
考点三 充分条件、必要条件的应用(典例迁移)
解 由p得(x-3a)(x-a)<0,当a<0时,3a由q得x2-x-6≤0或x2+2x-8>0,
则-2≤x≤3或x<-4或x>2,则x<-4或x≥-2.
设p:A=(3a,a),q:B=(-∞,-4)∪[-2,+∞),
又p是q的充分不必要条件.
补充例题3
考点三 充分条件、必要条件的应用(典例迁移)
解析 |x-1|因为不等式|x-1|所以(0,4) (1-a,1+a),
答案 D
考点三 充分条件、必要条件的应用(典例迁移)
可把充分条件、必要条件或充要条件转化为集合之间的关系,
1-a
1 + a
m-1
1 + m
解析 因为f(x)是偶函数,所以f(x)=f(|x|).
又y=f(x)在[0,+∞)上单调递增,
若a>|b|,则f(a)>f(|b|)=f(b),即充分性成立;
若f(a)>f(b),则等价为f(|a|)>f(|b|),即|a|>|b|,
即a>|b|或a<-|b|,即必要性不成立,
则“a>|b|”是“f(a)>f(b)”的充分不必要条件.
答案 A
布置作业
1.复习选修2-1,完成复习大书8-9页的知识梳理和诊断自测,拍照后发云
校家课前导学里
2.完成复习大书8-9页例1,训练1;例2-1,例2-2(2),训练2;例3(1),训练3.详细解答,拍照后发云校家课后作业里
1.2命题及其关系、充分条件与必要条件
第2课时
考点一 命题及其关系
解析①的否定是“ x∈R,x2-x+1>0”中是真命题,①正确;
②的否命题是“若x2+x-6<0,则x≤2”,
由x2+x-6<0,得-3
因此可知逆否命题为假命题,③错误.
综上可知,真命题是①,②.
答案 (2)C
原命题与逆否命题同真同假,逆命题与否命题同真同假
补充例题1
考点一 命题及其相互关系
考点一 命题及其相互关系
考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
即ab≤4,充分性成立;
当a=4,b=1时,满足ab≤4,
但a+b=5>4,不满足a+b≤4,
必要性不成立,
故“a+b≤4”是“ab≤4”的充分不必要条件.
答案 (1)A
考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
q
考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
解析 (2) (1)若m α,n α,m∥n,
由线面平行的判定定理知m∥α.
若m∥α,m α,n α,
不一定推出m∥n,直线m与n可能异面,
故“m∥n”是“m∥α”的充分不必要条件.
答案 (2)A
补充例题2
考点二 充分条件与必要条件的判定
考点二 充分条件与必要条件的判定
充要条件的判断可用 定义法:根据p q,q p进行判断.
解析 (1)由“x2-5x<0”可得“0
答案 (1)B
由0
充要条件的判断可用 定义法:根据p q,q p进行判断.
考点三 充分条件、必要条件的应用(典例迁移)
解 由x2-8x-20≤0,得-2≤x≤10,
∴P={x|-2≤x≤10}.
∵x∈P是x∈S的必要条件,则S P.
解得当0≤m≤3时,x∈P是x∈S的必要条件.
可把充分条件、必要条件或充要条件转化为集合之间的关系,
P
S
1-m
1+m
考点三 充分条件、必要条件的应用(典例迁移)
解 由例题知P={x|-2≤x≤10}.
∵¬P是¬S的必要不充分条件,
∴P是S的充分不必要条件,
∴ m≥9,则m的取值范围是[9,+∞).
可把充分条件、必要条件或充要条件转化为集合之间的关系,
S
1-m
1+m
P
考点三 充分条件、必要条件的应用(典例迁移)
解 由p得(x-3a)(x-a)<0,当a<0时,3a
则-2≤x≤3或x<-4或x>2,则x<-4或x≥-2.
设p:A=(3a,a),q:B=(-∞,-4)∪[-2,+∞),
又p是q的充分不必要条件.
补充例题3
考点三 充分条件、必要条件的应用(典例迁移)
解析 |x-1|因为不等式|x-1|
答案 D
考点三 充分条件、必要条件的应用(典例迁移)
可把充分条件、必要条件或充要条件转化为集合之间的关系,
1-a
1 + a
m-1
1 + m
解析 因为f(x)是偶函数,所以f(x)=f(|x|).
又y=f(x)在[0,+∞)上单调递增,
若a>|b|,则f(a)>f(|b|)=f(b),即充分性成立;
若f(a)>f(b),则等价为f(|a|)>f(|b|),即|a|>|b|,
即a>|b|或a<-|b|,即必要性不成立,
则“a>|b|”是“f(a)>f(b)”的充分不必要条件.
答案 A
布置作业
1.复习选修2-1,完成复习大书8-9页的知识梳理和诊断自测,拍照后发云
校家课前导学里
2.完成复习大书8-9页例1,训练1;例2-1,例2-2(2),训练2;例3(1),训练3.详细解答,拍照后发云校家课后作业里
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
