第14章《全等三角形》单元测试卷(附答案解析)
文档属性
| 名称 | 第14章《全等三角形》单元测试卷(附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 202.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-31 08:11:53 | ||
图片预览

文档简介
2013年沪科版八年级数学上册第14章《全等三角形》
单元测试卷(附答案解析)
(温馨提示:本卷满分150分,答题时间120分钟)
一.选择题(共10小题,满分40分,每小题4分)
1.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A. 20° B. 30° C. 35° D. 40°
2.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是( )
A. 5 B. 4 C. 3 D. 2
3.用两个全等的三角形一定不能拼出的图形是( )
A. 等腰三角形 B. 直角梯形 C. 菱形 D. 矩形
4.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,有以下结论:①AC=AE;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
5.我们把两个能够完全重合的图形称为全等图形,则下列命题中真命题是( )
A. 有一条边长对应相等的两个矩形是全等图形
B. 有一个内角对应相等的两个菱形是全等图形
C. 有两条对角线对应相等的两个矩形是全等图形
D. 有两条对角线对应相等的两个菱形是全等图形
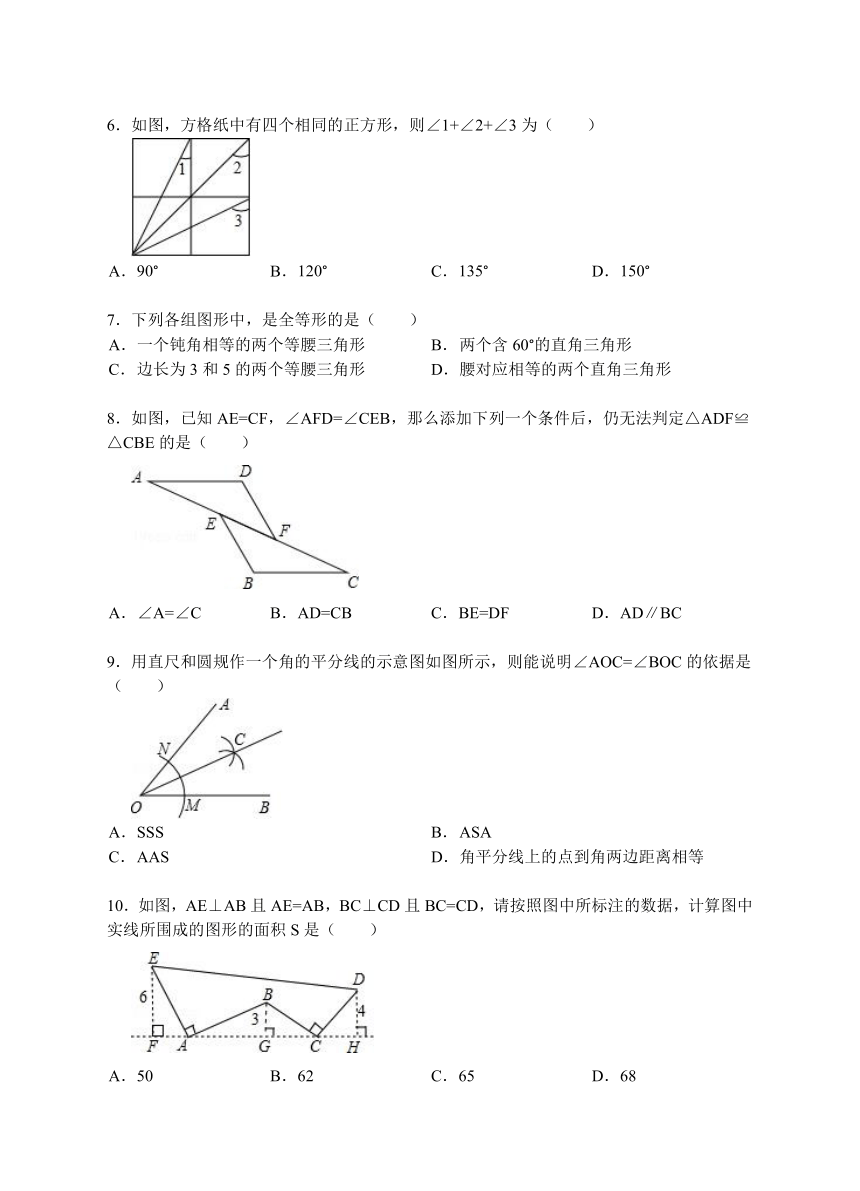
6.如图,方格纸中有四个相同的正方形,则∠1+∠2+∠3为( )
A. 90° B. 120° C. 135° D. 150°
7.下列各组图形中,是全等形的是( )
A. 一个钝角相等的两个等腰三角形 B. 两个含60°的直角三角形
C. 边长为3和5的两个等腰三角形 D. 腰对应相等的两个直角三角形
8.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A. ∠A=∠C B. AD=CB C. BE=DF D. AD∥BC
9.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A. SSS B. ASA
C. AAS D. 角平分线上的点到角两边距离相等
10.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A. 50 B. 62 C. 65 D. 68
二.填空题(共4小题,满分20分,每小题5分)
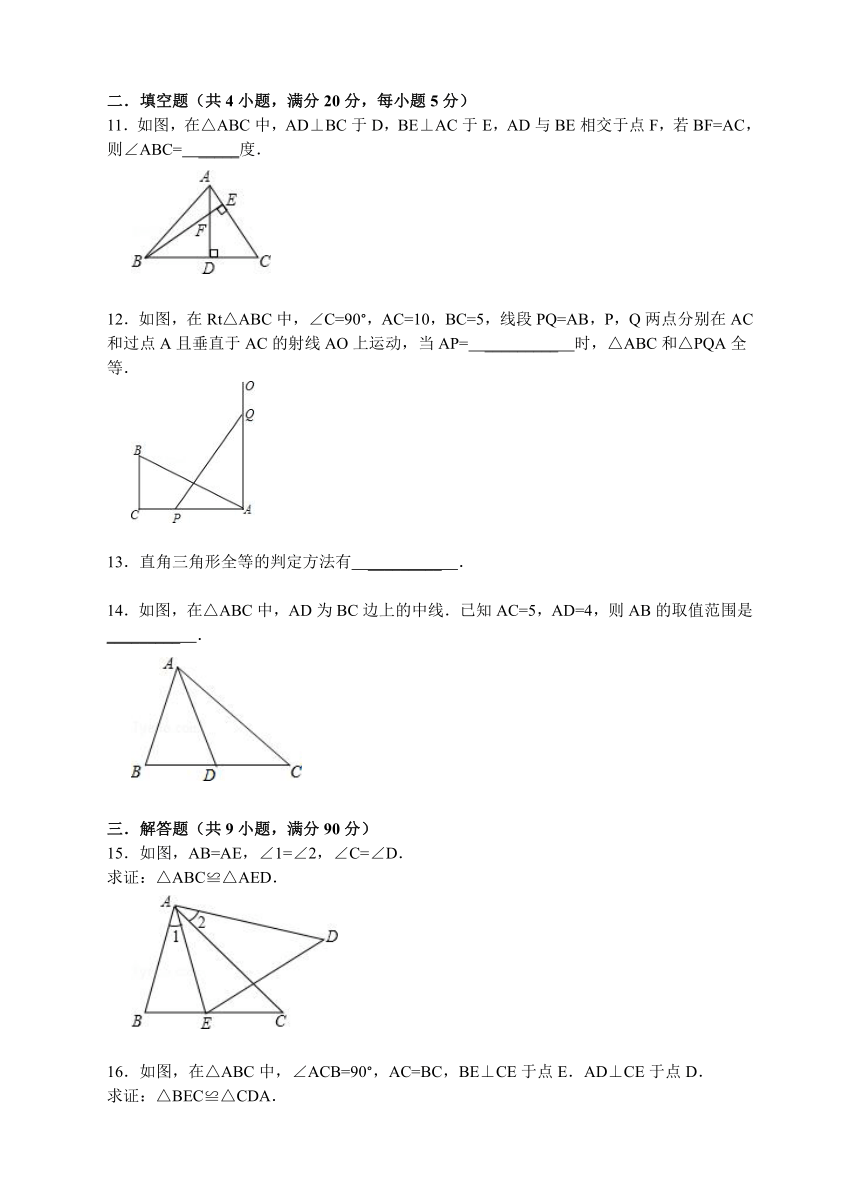
11.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC= _____度.
12.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP= _________ 时,△ABC和△PQA全等.
13.直角三角形全等的判定方法有 _________ .
14.如图,在△ABC中,AD为BC边上的中线.已知AC=5,AD=4,则AB的取值范围是 _________ .
三.解答题(共9小题,满分90分)
15.如图,AB=AE,∠1=∠2,∠C=∠D.
求证:△ABC≌△AED.
16.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E.AD⊥CE于点D.
求证:△BEC≌△CDA.
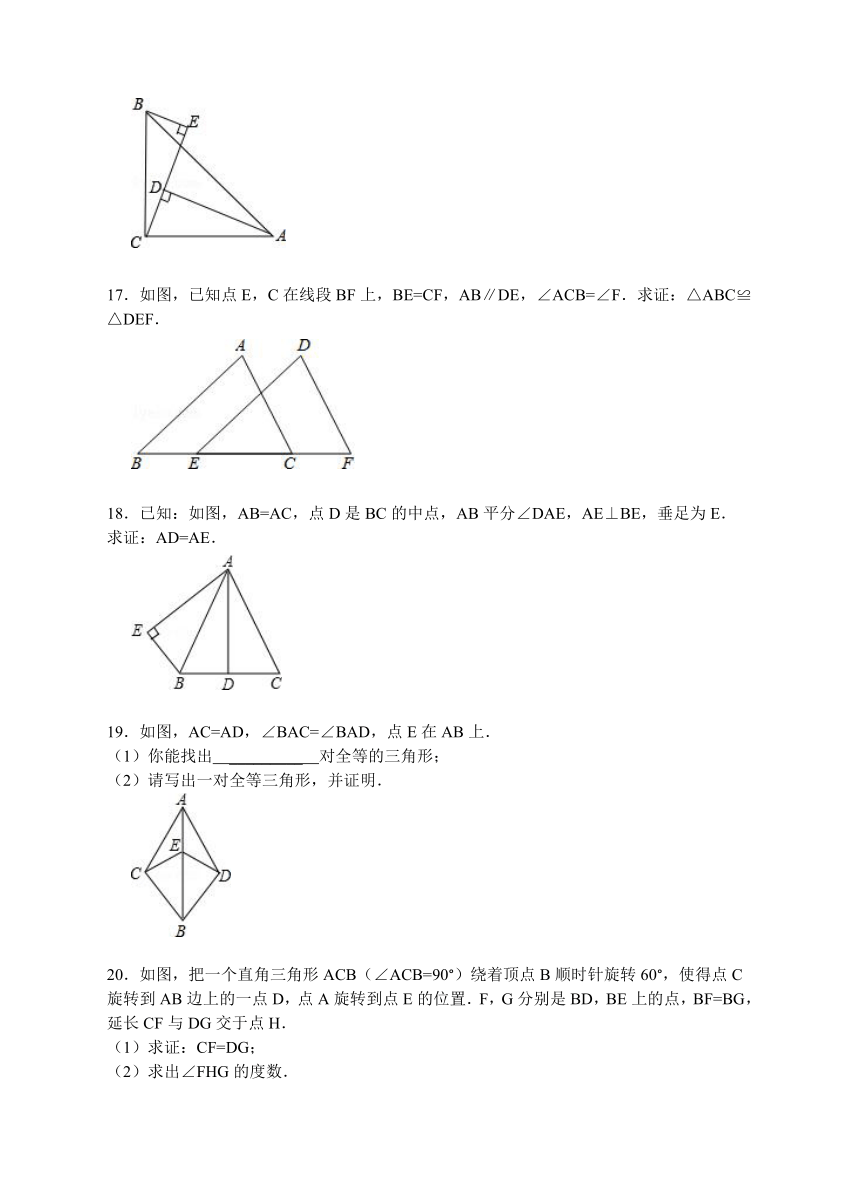
17.如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.
18.已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
求证:AD=AE.
19.如图,AC=AD,∠BAC=∠BAD,点E在AB上.
(1)你能找出 _________ 对全等的三角形;
(2)请写出一对全等三角形,并证明.
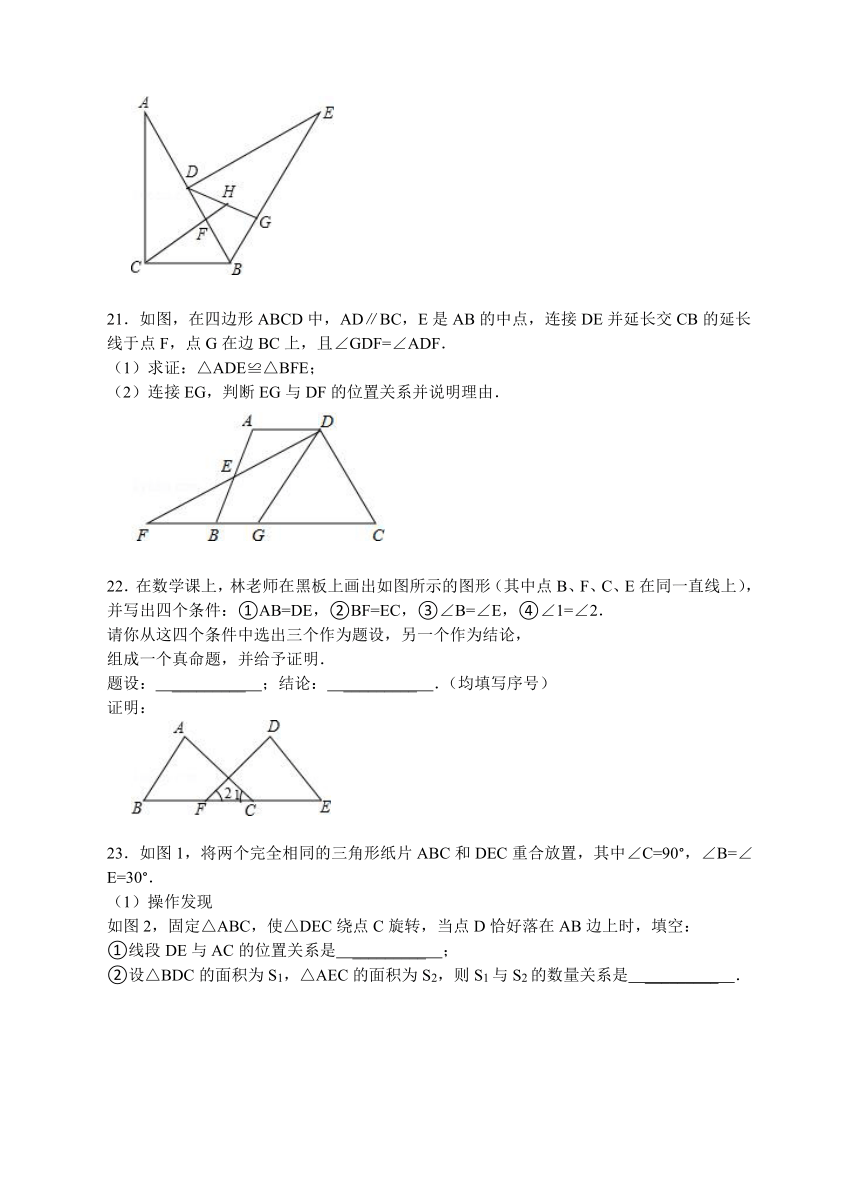
20.如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG;
(2)求出∠FHG的度数.
21.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
22.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,
组成一个真命题,并给予证明.
题设: _________ ;结论: _________ .(均填写序号)
证明:
23.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是 _________ ;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 _________ .
(2)猜想论证
当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是角平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B B D C D B A A
解析:
1. 解:∵△ACB≌△A′CB′∴∠ACB=∠A′CB′即∠ACA′+∠A′CB=∠B′CB+∠A′CB,∴∠ACA′=∠B′CB,又∠B′CB=30°∴∠ACA′=30°.故选B.
2. 解:∵△ABC≌△DEF∴DE=AB∵BE=4,AE=1∴DE=AB=BE+AE=4+1=5故选A.
3. 解:用两个全等的直角三角形就能拼出等腰三角形,A可以;如图两个全等的正三角形就可以拼出菱形,C可以;两个全等的直角三角形时就可以拼出矩形,D可以;不管用什么形状的两个全等的三角形不管怎样也拼不出直角梯形.故选B.
4. 解:∵△ABC≌△AEF,AB=AE,∠B=∠E∴EF=BC,∠EAF=∠BAC∴∠EAB+∠BAF=∠FAC+∠BAF即∠EAB=∠FACAC与AE不是对应边,不能求出二者相等,也不能求出∠FAB=∠EAB∴①、②错误,③、④正确故选B.
5. 解:A、有一条边长对应相等的两个矩形是全等图形,命题不正确,故本选项错误;B、有一个内角对应相等的两个菱形是全等图形,命题不正确,故本选项错误;C、有两条对角线对应相等的两个矩形是全等图形,命题不正确,故本选项错误;D、两条对角线对应相等的两个菱形是全等图形,是真命题,故本选项正确.故选D.
6. 解:∵,∴△ACB≌△BDE,∠1所在的三角形与∠3所在的三角形全等,∴∠1+∠3=90°,又∠2=45°,∴∠1+∠2+∠3=135°.故选:C.
7. 解:A、不能确定边长相等,故本选项错误;B、不能确定边长相等,故本选项错误;C、边长为3和5的两个等腰三角形不能确定那个边为腰,故本选项错误;D、腰对应相等的两个直角三角形一定是全等三角形,故本选项正确.故选D.
8. 解:∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,A、∵在△ADF和△CBE中∴△ADF≌△CBE(ASA),正确,故本选项错误;B、根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项正确;C、∵在△ADF和△CBE中∴△ADF≌△CBE(SAS),正确,故本选项错误;D、∵AD∥BC,∴∠A=∠C,∵在△ADF和△CBE中∴△ADF≌△CBE(ASA),正确,故本选项错误;故选B.
9. 解:连接NC,MC,在△ONC和△OMC中,∴△ONC≌△OMC(SSS),∴∠AOC=∠BOC,故选A.
10. 解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH ∠EAB=∠EFA=∠BGA=90°,∠EAF+∠BAG=90°,∠ABG+∠BAG=90° ∠EAF=∠ABG,∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG △EFA≌△ABG∴AF=BG,AG=EF.同理证得△BGC≌△DHC得GC=DH,CH=BG.故FH=FA+AG+GC+CH=3+6+4+3=16故S=(6+4)×16﹣3×4﹣6×3=50.故选A.
二.填空题(共4小题,满分20分,每小题5分)
11. 45
解:∵AD⊥BC于D,BE⊥AC于E∴∠EAF+∠AFE=90°,∠DBF+∠BFD=90°,又∵∠BFD=∠AFE(对顶角相等)∴∠EAF=∠DBF,在Rt△ADC和Rt△BDF中,,∴△ADC≌△BDF(AAS),∴BD=AD,即∠ABC=∠BAD=45°.故答案为:45
12. 5或10
解:当AP=5或10时,△ABC和△PQA全等,理由是:∵∠C=90°,AO⊥AC,∴∠C=∠QAP=90°,①当AP=5=BC时,在Rt△ACB和Rt△QAP中∴Rt△ACB≌Rt△QAP(HL),②当AP=10=AC时,在Rt△ACB和Rt△PAQ中∴Rt△ACB≌Rt△PAQ(HL),故答案为:5或10.
13. HL,AAS,SAS,ASA.SSS. .
解:直角三角形全等的判定除了HL 外,其它四种方法也适用,所以直角三角形全等的判定方法有HL,AAS,SAS,ASA.SSS.故填:HL,AAS,SAS,ASA.SSS.
14. 3<AB<13 .
解:延长AD到E,使DE=AD,连接CE,则AE=2AD=2×4=8,∵AD是BC边上的中线,∴BD=CD,∵在△ABD和△ECD中,,∴△ABD≌△ECD(SAS),∴CE=AB,又∵AC=5,∴5+8=13,8﹣5=3,∴3<CE<13,即AB的取值范围是:3<AB<13.故答案为:3<AB<13.
三.解答题(共9小题,满分90分)
15. 证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD,∵在△ABC和△AED中,,∴△ABC≌△AED(AAS).
16. 证明:∵BE⊥CE于E,AD⊥CE于D,∴∠BEC=∠CDA=90°,在Rt△BEC中,∠BCE+∠CBE=90°,在Rt△BCA中,∠BCE+∠ACD=90°,∴∠CBE=∠ACD,在△BEC和△CDA中,∠BEC=∠CDA,∠CBE=∠ACD,BC=AC,∴△BEC≌△CDA.
17. 证明:∵AB∥DE,∴∠B=∠DEF.∵BE=CF,∴BC=EF.∵∠ACB=∠F,∴,∴△ABC≌△DEF(ASA).
18. 证明:∵AB=AC,点D是BC的中点,∴∠ADB=90°,∵AE⊥EB,∴∠E=∠ADB=90°,∵AB平分∠DAE,∴∠1=∠2;在△ADB和△AEB中,,∴△ADB≌△AEB(AAS),∴AD=AE.
19. 解:(1)△ABC≌△ABD(SAS),△BCE≌△BED,△ACE≌△AED,故有3对.(2)△ABC≌△ABD,证明:在△ABC和△ABD中,,∴△ABC≌△ABD(SAS).
20. (1)证明:∵在△CBF和△DBG中,,∴△CBF≌△DBG(SAS),∴CF=DG;(2)解:∵△CBF≌△DBG,∴∠BCF=∠BDG,又∵∠CFB=∠DFH,∴∠DHF=∠CBF=60°,∴∠FHG=180°﹣∠DHF=180°﹣60°=120°.
21. (1)证明:∵AD∥BC,∴∠ADE=∠BFE,∵E为AB的中点,∴AE=BE,在△AED和△BFE中,,∴△AED≌△BFE(AAS);(2)解:EG与DF的位置关系是EG⊥DF,理由为:连接EG,∵∠GDF=∠ADE,∠ADE=∠BFE,∴∠GDF=∠BFE,由(1)△AED≌△BFE得:DE=EF,即GE为DF上的中线,∴GE垂直平分DF.
22. 情况一:题设:①②③;结论:④.证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF.在△ABC和△DEF中,,∴△ABC≌△DEF(SAS),∴∠1=∠2;情况二:题设:①③④;结论:②. 证明:在△ABC和△DEF中,∵,∴△ABC≌△DEF(AAS),∴BC=EF,∴BC﹣FC=EF﹣FC,即BF=EC;情况三:题设:②③④;结论:①.证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),∴AB=DE.
23. 解:(1)①∵△DEC绕点C旋转点D恰好落在AB边上,∴AC=CD,∵∠BAC=90°﹣∠B=90°﹣30°=60°,∴△ACD是等边三角形,∴∠ACD=60°,又∵∠CDE=∠BAC=60°,∴∠ACD=∠CDE,∴DE∥AC;②∵∠B=30°,∠C=90°,∴CD=AC=AB,∴BD=AD=AC,根据等边三角形的性质,△ACD的边AC、AD上的高相等,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;故答案为:DE∥AC;S1=S2;(2)如图,∵△DEC是由△ABC绕点C旋转得到,∴BC=CE,AC=CD,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,∵在△ACN和△DCM中,,∴△ACN≌△DCM(AAS),∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;(3)如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,所以BE=DF1,且BE、DF1上的高相等,此时S△DCF=S△BDE,过点D作DF2⊥BD,∵∠ABC=60°,∴∠F1DF2=∠ABC=60°,∴△DF1F2是等边三角形,∴DF1=DF2,∵BD=CD,∠ABC=60°,点D是角平分线上一点,∴∠DBC=∠DCB=×60°=30°,∴∠CDF1=180°﹣30°=150°,∠CDF2=360°﹣150°﹣60°=150°,∴∠CDF1=∠CDF2,∵在△CDF1和△CDF2中,,∴△CDF1≌△CDF2(SAS),∴点F2也是所求的点,∵∠ABC=60°,点D是角平分线上一点,DE∥AB,∴∠DBC=∠BDE=∠ABD=×60°=30°,又∵BD=4,∴BE=×4÷cos30°=2÷=,∴BF1=,BF2=BF1+F1F2=+=,故BF的长为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
单元测试卷(附答案解析)
(温馨提示:本卷满分150分,答题时间120分钟)
一.选择题(共10小题,满分40分,每小题4分)
1.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A. 20° B. 30° C. 35° D. 40°
2.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是( )
A. 5 B. 4 C. 3 D. 2
3.用两个全等的三角形一定不能拼出的图形是( )
A. 等腰三角形 B. 直角梯形 C. 菱形 D. 矩形
4.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,有以下结论:①AC=AE;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
5.我们把两个能够完全重合的图形称为全等图形,则下列命题中真命题是( )
A. 有一条边长对应相等的两个矩形是全等图形
B. 有一个内角对应相等的两个菱形是全等图形
C. 有两条对角线对应相等的两个矩形是全等图形
D. 有两条对角线对应相等的两个菱形是全等图形
6.如图,方格纸中有四个相同的正方形,则∠1+∠2+∠3为( )
A. 90° B. 120° C. 135° D. 150°
7.下列各组图形中,是全等形的是( )
A. 一个钝角相等的两个等腰三角形 B. 两个含60°的直角三角形
C. 边长为3和5的两个等腰三角形 D. 腰对应相等的两个直角三角形
8.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A. ∠A=∠C B. AD=CB C. BE=DF D. AD∥BC
9.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A. SSS B. ASA
C. AAS D. 角平分线上的点到角两边距离相等
10.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A. 50 B. 62 C. 65 D. 68
二.填空题(共4小题,满分20分,每小题5分)
11.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC= _____度.
12.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP= _________ 时,△ABC和△PQA全等.
13.直角三角形全等的判定方法有 _________ .
14.如图,在△ABC中,AD为BC边上的中线.已知AC=5,AD=4,则AB的取值范围是 _________ .
三.解答题(共9小题,满分90分)
15.如图,AB=AE,∠1=∠2,∠C=∠D.
求证:△ABC≌△AED.
16.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E.AD⊥CE于点D.
求证:△BEC≌△CDA.
17.如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.
18.已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
求证:AD=AE.
19.如图,AC=AD,∠BAC=∠BAD,点E在AB上.
(1)你能找出 _________ 对全等的三角形;
(2)请写出一对全等三角形,并证明.
20.如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG;
(2)求出∠FHG的度数.
21.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
22.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,
组成一个真命题,并给予证明.
题设: _________ ;结论: _________ .(均填写序号)
证明:
23.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是 _________ ;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 _________ .
(2)猜想论证
当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是角平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B B D C D B A A
解析:
1. 解:∵△ACB≌△A′CB′∴∠ACB=∠A′CB′即∠ACA′+∠A′CB=∠B′CB+∠A′CB,∴∠ACA′=∠B′CB,又∠B′CB=30°∴∠ACA′=30°.故选B.
2. 解:∵△ABC≌△DEF∴DE=AB∵BE=4,AE=1∴DE=AB=BE+AE=4+1=5故选A.
3. 解:用两个全等的直角三角形就能拼出等腰三角形,A可以;如图两个全等的正三角形就可以拼出菱形,C可以;两个全等的直角三角形时就可以拼出矩形,D可以;不管用什么形状的两个全等的三角形不管怎样也拼不出直角梯形.故选B.
4. 解:∵△ABC≌△AEF,AB=AE,∠B=∠E∴EF=BC,∠EAF=∠BAC∴∠EAB+∠BAF=∠FAC+∠BAF即∠EAB=∠FACAC与AE不是对应边,不能求出二者相等,也不能求出∠FAB=∠EAB∴①、②错误,③、④正确故选B.
5. 解:A、有一条边长对应相等的两个矩形是全等图形,命题不正确,故本选项错误;B、有一个内角对应相等的两个菱形是全等图形,命题不正确,故本选项错误;C、有两条对角线对应相等的两个矩形是全等图形,命题不正确,故本选项错误;D、两条对角线对应相等的两个菱形是全等图形,是真命题,故本选项正确.故选D.
6. 解:∵,∴△ACB≌△BDE,∠1所在的三角形与∠3所在的三角形全等,∴∠1+∠3=90°,又∠2=45°,∴∠1+∠2+∠3=135°.故选:C.
7. 解:A、不能确定边长相等,故本选项错误;B、不能确定边长相等,故本选项错误;C、边长为3和5的两个等腰三角形不能确定那个边为腰,故本选项错误;D、腰对应相等的两个直角三角形一定是全等三角形,故本选项正确.故选D.
8. 解:∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,A、∵在△ADF和△CBE中∴△ADF≌△CBE(ASA),正确,故本选项错误;B、根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项正确;C、∵在△ADF和△CBE中∴△ADF≌△CBE(SAS),正确,故本选项错误;D、∵AD∥BC,∴∠A=∠C,∵在△ADF和△CBE中∴△ADF≌△CBE(ASA),正确,故本选项错误;故选B.
9. 解:连接NC,MC,在△ONC和△OMC中,∴△ONC≌△OMC(SSS),∴∠AOC=∠BOC,故选A.
10. 解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH ∠EAB=∠EFA=∠BGA=90°,∠EAF+∠BAG=90°,∠ABG+∠BAG=90° ∠EAF=∠ABG,∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG △EFA≌△ABG∴AF=BG,AG=EF.同理证得△BGC≌△DHC得GC=DH,CH=BG.故FH=FA+AG+GC+CH=3+6+4+3=16故S=(6+4)×16﹣3×4﹣6×3=50.故选A.
二.填空题(共4小题,满分20分,每小题5分)
11. 45
解:∵AD⊥BC于D,BE⊥AC于E∴∠EAF+∠AFE=90°,∠DBF+∠BFD=90°,又∵∠BFD=∠AFE(对顶角相等)∴∠EAF=∠DBF,在Rt△ADC和Rt△BDF中,,∴△ADC≌△BDF(AAS),∴BD=AD,即∠ABC=∠BAD=45°.故答案为:45
12. 5或10
解:当AP=5或10时,△ABC和△PQA全等,理由是:∵∠C=90°,AO⊥AC,∴∠C=∠QAP=90°,①当AP=5=BC时,在Rt△ACB和Rt△QAP中∴Rt△ACB≌Rt△QAP(HL),②当AP=10=AC时,在Rt△ACB和Rt△PAQ中∴Rt△ACB≌Rt△PAQ(HL),故答案为:5或10.
13. HL,AAS,SAS,ASA.SSS. .
解:直角三角形全等的判定除了HL 外,其它四种方法也适用,所以直角三角形全等的判定方法有HL,AAS,SAS,ASA.SSS.故填:HL,AAS,SAS,ASA.SSS.
14. 3<AB<13 .
解:延长AD到E,使DE=AD,连接CE,则AE=2AD=2×4=8,∵AD是BC边上的中线,∴BD=CD,∵在△ABD和△ECD中,,∴△ABD≌△ECD(SAS),∴CE=AB,又∵AC=5,∴5+8=13,8﹣5=3,∴3<CE<13,即AB的取值范围是:3<AB<13.故答案为:3<AB<13.
三.解答题(共9小题,满分90分)
15. 证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD,∵在△ABC和△AED中,,∴△ABC≌△AED(AAS).
16. 证明:∵BE⊥CE于E,AD⊥CE于D,∴∠BEC=∠CDA=90°,在Rt△BEC中,∠BCE+∠CBE=90°,在Rt△BCA中,∠BCE+∠ACD=90°,∴∠CBE=∠ACD,在△BEC和△CDA中,∠BEC=∠CDA,∠CBE=∠ACD,BC=AC,∴△BEC≌△CDA.
17. 证明:∵AB∥DE,∴∠B=∠DEF.∵BE=CF,∴BC=EF.∵∠ACB=∠F,∴,∴△ABC≌△DEF(ASA).
18. 证明:∵AB=AC,点D是BC的中点,∴∠ADB=90°,∵AE⊥EB,∴∠E=∠ADB=90°,∵AB平分∠DAE,∴∠1=∠2;在△ADB和△AEB中,,∴△ADB≌△AEB(AAS),∴AD=AE.
19. 解:(1)△ABC≌△ABD(SAS),△BCE≌△BED,△ACE≌△AED,故有3对.(2)△ABC≌△ABD,证明:在△ABC和△ABD中,,∴△ABC≌△ABD(SAS).
20. (1)证明:∵在△CBF和△DBG中,,∴△CBF≌△DBG(SAS),∴CF=DG;(2)解:∵△CBF≌△DBG,∴∠BCF=∠BDG,又∵∠CFB=∠DFH,∴∠DHF=∠CBF=60°,∴∠FHG=180°﹣∠DHF=180°﹣60°=120°.
21. (1)证明:∵AD∥BC,∴∠ADE=∠BFE,∵E为AB的中点,∴AE=BE,在△AED和△BFE中,,∴△AED≌△BFE(AAS);(2)解:EG与DF的位置关系是EG⊥DF,理由为:连接EG,∵∠GDF=∠ADE,∠ADE=∠BFE,∴∠GDF=∠BFE,由(1)△AED≌△BFE得:DE=EF,即GE为DF上的中线,∴GE垂直平分DF.
22. 情况一:题设:①②③;结论:④.证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF.在△ABC和△DEF中,,∴△ABC≌△DEF(SAS),∴∠1=∠2;情况二:题设:①③④;结论:②. 证明:在△ABC和△DEF中,∵,∴△ABC≌△DEF(AAS),∴BC=EF,∴BC﹣FC=EF﹣FC,即BF=EC;情况三:题设:②③④;结论:①.证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),∴AB=DE.
23. 解:(1)①∵△DEC绕点C旋转点D恰好落在AB边上,∴AC=CD,∵∠BAC=90°﹣∠B=90°﹣30°=60°,∴△ACD是等边三角形,∴∠ACD=60°,又∵∠CDE=∠BAC=60°,∴∠ACD=∠CDE,∴DE∥AC;②∵∠B=30°,∠C=90°,∴CD=AC=AB,∴BD=AD=AC,根据等边三角形的性质,△ACD的边AC、AD上的高相等,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;故答案为:DE∥AC;S1=S2;(2)如图,∵△DEC是由△ABC绕点C旋转得到,∴BC=CE,AC=CD,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,∵在△ACN和△DCM中,,∴△ACN≌△DCM(AAS),∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;(3)如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,所以BE=DF1,且BE、DF1上的高相等,此时S△DCF=S△BDE,过点D作DF2⊥BD,∵∠ABC=60°,∴∠F1DF2=∠ABC=60°,∴△DF1F2是等边三角形,∴DF1=DF2,∵BD=CD,∠ABC=60°,点D是角平分线上一点,∴∠DBC=∠DCB=×60°=30°,∴∠CDF1=180°﹣30°=150°,∠CDF2=360°﹣150°﹣60°=150°,∴∠CDF1=∠CDF2,∵在△CDF1和△CDF2中,,∴△CDF1≌△CDF2(SAS),∴点F2也是所求的点,∵∠ABC=60°,点D是角平分线上一点,DE∥AB,∴∠DBC=∠BDE=∠ABD=×60°=30°,又∵BD=4,∴BE=×4÷cos30°=2÷=,∴BF1=,BF2=BF1+F1F2=+=,故BF的长为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
