3.3 角的度量(,含解答)[上学期]
文档属性
| 名称 | 3.3 角的度量(,含解答)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 63.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-15 00:00:00 | ||
图片预览


文档简介
3.3 角的度量 ( http: / / )
A卷 基础知识达标
(45分钟 100分)
一、选择题(每题4分,共32分)
1.如图1所示,从点O出发的5条射线,可以组成的角的个数是( ).
A.4 B.6 C.8 D.10
2.下列语句,正确的是( ).
A.直线可表示一个平角; B.平角的两边向左右无限延伸;
C.延长线段AB至点C,则∠ACB=180°;
D.在一条直线上顺次取三点A、B、C,则∠ABC=180° (1)
3.射线OA和射线OB是一个角的两边,这个角可记为( ).
A.∠AOB B.∠BAO C.∠OBA D.∠OAB
4.角度是( )进制.
A.二 B.八 C.十 D.六十
5.0.25°等于( )分.
A.60 B.15 C.90 D.360
6.下面语句中,正确的是( ).
A.两个互补的角是平角; B.一条直线就是一个平角;
C.两条直线相交,形成4个小于平角的角;
D.点A、B分别在∠O的两条边上,则它们到点O的距离越大,∠O也越大.
7.钟表在5点30分时,它的时针和分针所成的锐角是( ).
A.15° B.70° C.30° D.90°
8.学校、电影院、公园的平面图上的标点分别是A、B、C,电影院在学校的正东方向,公园在学校的南偏西25°方向,那么平面图上的∠CAB等于( ).
A.115° B.25° C.155° D.65°
二、填空题(每题3分,共21分)
9.钟表的时间为2时整,时针与分针所夹的角是_____度.
10.如图2所示,图中共有______条线段,______个小于平角的角.
(2) (3) (4) (5)
11.如图3中以A为顶点的角的个数,与直线L上线段的条数_______(填“相等”或“不相等”).
12.如图4中∠AOB的两边与直线L_______(填“相交”或“不相交”).
13.43°29′47″+36°30′13″=__________,23°30′=_______°,13.6°=_______°________′.
14.如图5所示,∠BAD=_______+______,∠AOC=______+______,我们也把∠AOC叫做________角.
15.时钟的分针1小时转_______度,时针1小时转______度;时钟的分针1分钟转_______度,时针1分钟转________度.
三、计算题:(每题5分,共15分).
16.36.32°=_______°_______′________″.
17.52°25′12″=_________°.
18.180°-(22°30′42″+67°20′20″)=______=_____°_____′______″.
四、解答题(每题8分,共40分)
19.若时钟由2点30分走到2点55分,问时针、分针各转过多大的角度?
20.在8点与9点之间,分针与时针重合的时刻是几点几分?
21.试用等腰三角板和一个30°,60°的三角板画出15°,135°的角.
22.两个角的和为67°56′,差是12°40′,求这两个角.
B卷 发散创新应用
(45分钟 100分)
一、综合题(1题20分,2题10分,共30分)
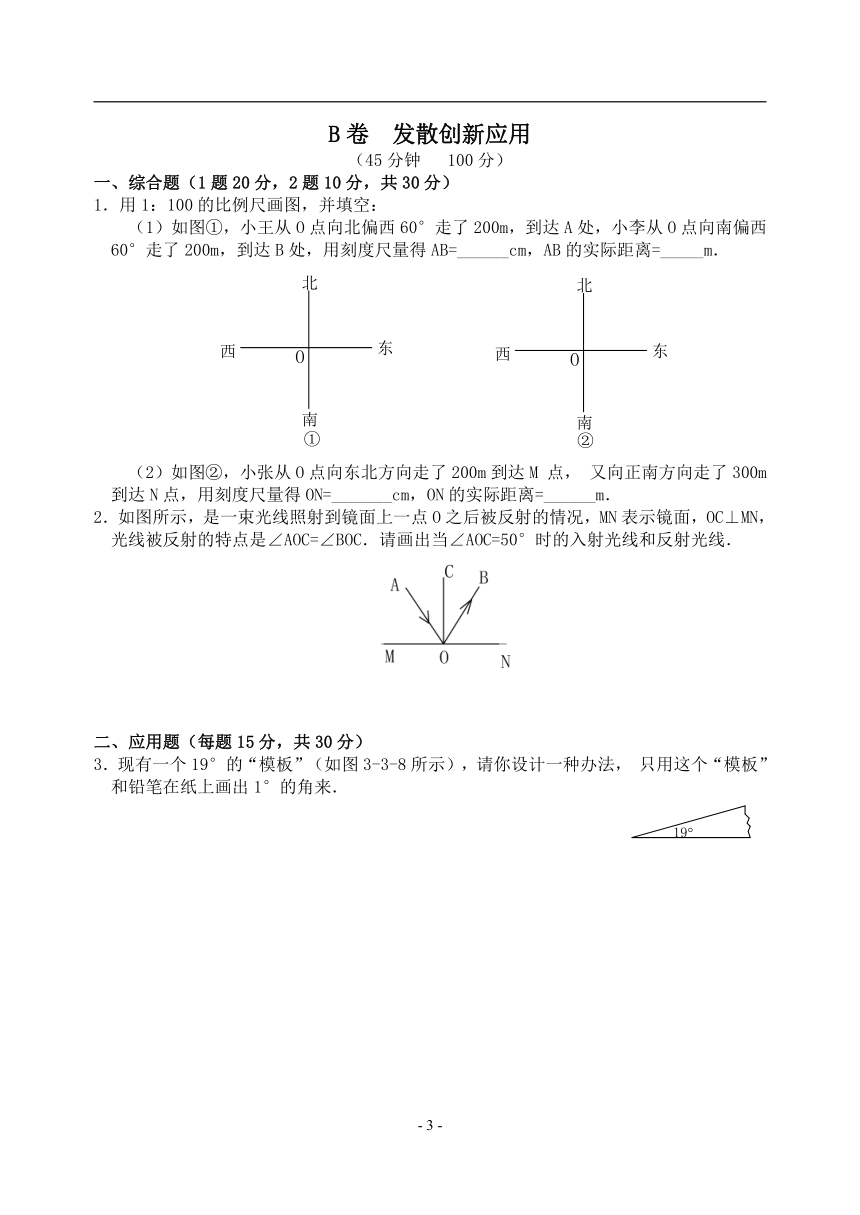
1.用1:100的比例尺画图,并填空:
(1)如图①,小王从O点向北偏西60°走了200m,到达A处,小李从O点向南偏西60°走了200m,到达B处,用刻度尺量得AB=______cm,AB的实际距离=_____m.
(2)如图②,小张从O点向东北方向走了200m到达M点,又向正南方向走了300m到达N点,用刻度尺量得ON=_______cm,ON的实际距离=______m.
2.如图所示,是一束光线照射到镜面上一点O之后被反射的情况,MN表示镜面,OC⊥MN,光线被反射的特点是∠AOC=∠BOC.请画出当∠AOC=50°时的入射光线和反射光线.
二、应用题(每题15分,共30分)
3.现有一个19°的“模板”(如图3-3-8所示),请你设计一种办法,只用这个“模板”和铅笔在纸上画出1°的角来.
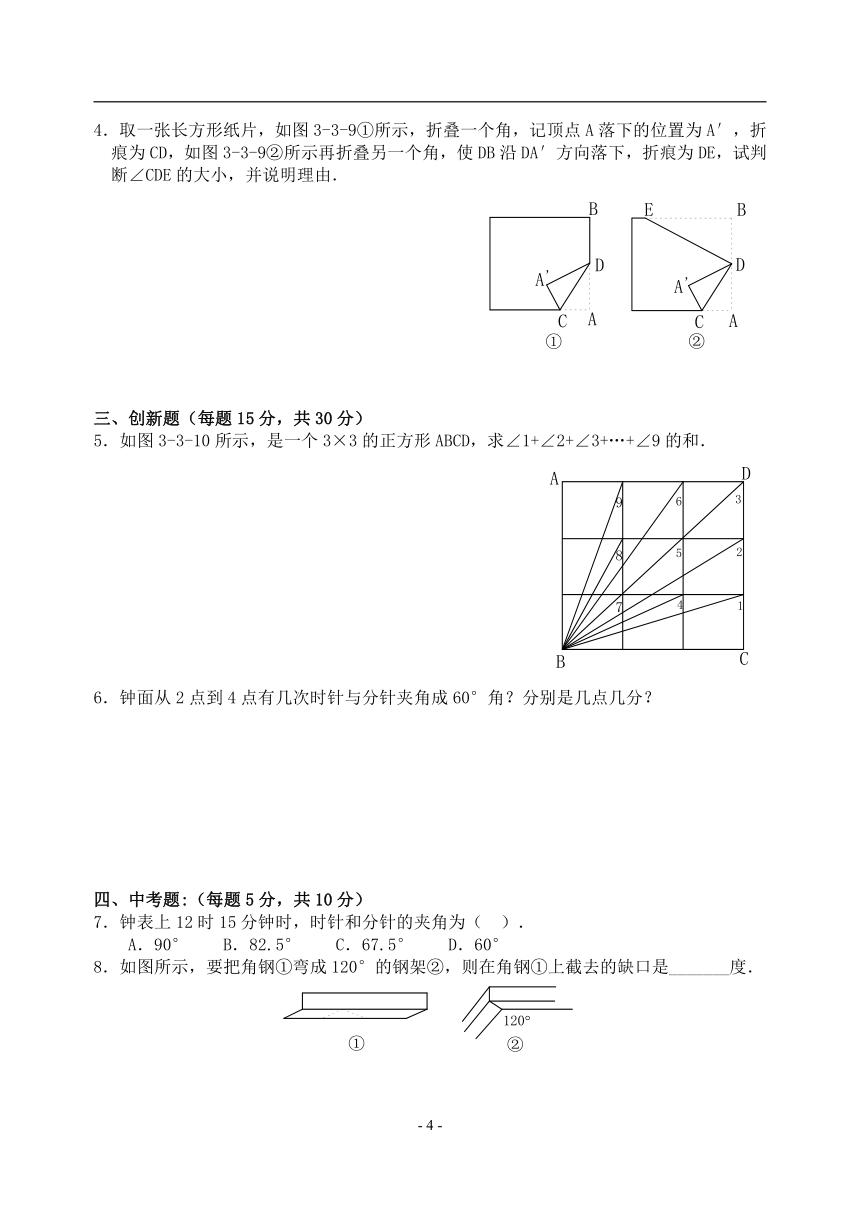
4.取一张长方形纸片,如图3-3-9①所示,折叠一个角,记顶点A落下的位置为A′,折痕为CD,如图3-3-9②所示再折叠另一个角,使DB沿DA′方向落下,折痕为DE,试判断∠CDE的大小,并说明理由.
三、创新题(每题15分,共30分)
5.如图3-3-10所示,是一个3×3的正方形ABCD,求∠1+∠2+∠3+…+∠9的和.
6.钟面从2点到4点有几次时针与分针夹角成60°角?分别是几点几分?
四、中考题:(每题5分,共10分)
7.钟表上12时15分钟时,时针和分针的夹角为( ).
A.90° B.82.5° C.67.5° D.60°
8.如图所示,要把角钢①弯成120°的钢架②,则在角钢①上截去的缺口是_______度.
答案:
A卷
一、
1.D 分析:假设图中所成的角以OA为始边,那么OB、OC、OD、OE可以成为角的终边,这样可以构成∠AOB、∠AOC、∠AOD和∠AOE;以OC为始边,则可构成∠BOC、∠BOD和∠BOE;以OC为始边,则可构成∠COD和∠COE;以OD为始边,则可构成∠DOE,这样共可组成角的个数为10个. 点拨:不要重复数,也不要漏掉.
2.D 分析:角的构成有三要素,故A项中只有边而没有顶点,不符合题意.角的两边都是射线,只能向一方延伸,而不能向左右延伸,故B项错误.延长线段AB至点C,则AC边与BC边重合,∠ACB=0°,故不可能为180°.D项中A、B、C三点在一条直线上,且A、C两点在B点的两边,构成一个平角,故D项符合题意.
3.A 分析:角的表示通常为:用三个大写的英文字母和“∠”表示,中间字母是角的顶点,其他两个字母分别是表示角的两边上的点.当一个点作为多个角的顶点时,常用此种方法表示.因此,点O一定是中间的字母,故选A.
4.D 点拨:角度制常以度、分、秒为单位.而度、分、秒之间换算单位是60.
5.B 分析:一个周角为360°,把1度的角60等分,每一份叫做1分的角,
故0.25°=0.25×60分=15分.
6.C 分析:两个互补的角是两个角,平角是一个角;
两直线相交,确实形成4个小于平角的角.
7.A 分析:钟表时针旋转一周为360°,共12时辰,
则每邻近两个时辰所夹的角为360°÷12=30°,
当钟表为5时30分钟时,时针正好位于5时和6时中间,
而分针正指6时,此时时针和分针所夹角为:30°÷2=15°,
故A为正确答案.
8.A 分析:如右图,一平面内以学校A为中点,
则正东与正南所成的角为360°÷=90°,
而公园C在学校A的南偏西25°,
则∠CAB=90°+25°=115°,
故A符合题意.
二、
9.60 分析:钟表盘上每邻近两个时辰所夹的角为360°÷12=30°,
当钟表为2时整时,时针指向“2”,
而分针指向“12”,那么时针和分针所夹角为2×30°=60°.
10.7 8 点拨:关键是与点A有关的线段与小于平角的角的数目.
11.相等 分析:每一个以A为顶点的角,其两边都在直线L上截得一条线段.
12.相交 分析:角的两边是射线,直线L更是向两边无限伸展的.
13.80° 23.5° 13 36
分析:把一个周角360等分,每一份都是1度的角,记作1°;
把1度的角60等分,每一份叫做1分的角,记作1′;
把1分的角60等分,每一份叫做1秒的角,记作1″,
故43°29′47″+36°30′13″=79°59′60″=79°60′=80°,
23°30′=23.5°,13.6°=13°+0.6×60′=13°36′.
14.∠BAC ∠CAD ∠AOD ∠DOC 平
分析:射线OC是以∠BAD中A为顶点的一条射线,它把∠BAD分成了两个角:∠BAC∠和∠CAD.同理,射线OD也把∠AOC分成了两个角:∠AOD与∠DOC.∠AOC的两边OA与OC均在一条直线上,故∠AOC=180°.
15.360 30 6 0.5
分析:时钟的分针1小时转一周为360°,
则分针1分钟转的度数为360°÷60=6°,时针1小时(60分钟)转30°,
则1分钟转的度数=30°÷60=0.5°.
三、
16.36°19′12″
点拨:把度化为度、分、秒,必须先把不足1度的化为分,再把不足1分的化为秒,也就是把角的度量单位由大小的过程,每步要乘60′和60″.
17.52.42° 点拨:把度、分、秒化为度,必须把秒化为分,然后再加上原有的分,再化为度,也就是把角的度量单位由小化大的过程,每步要乘()°或()′.
18.180°-89°51′2″ 90°8′58″
点拨:角的加减运算,必须把度、分、秒分别相加减,
进位时,60″=1′,60′=1°,借位时,1°=60′,1′=60″.
四、
19.150° 12.5°
解:分针所走度数:×(55-30)=6°×25=150°,
时针所走度数:×(55-30)==12.5°.
20.分针与时针重合的时刻是8点43分
分析:在8点整时,时针与分针成240°,
设分针与时针重合是在8点x分.
因为分针每分钟转动一小格,即6°,所以分针共转动(6x)°,
而时针转动的速度只有分针的,即()°,
依题意有:6x-=240,
所以x==43分.即分针与时针重合的时刻是在8点43分.
21.分析:先用等腰三角板画出一个45°的角∠AOB,以O为顶点,OB为始边,
用30°,60°的三角板作出∠BOC=60°,则∠AOC=15°,
如上图(1),先作出一个45°的角,∠AOB=45°,反向延长OA至C,则∠BOC=135°.
如上图(2).
22.这两个角分别是40°18′,27°38′
分析:设这两个角分别为x,y,则
所以x==40°18′,y=67°56′-40°18′=27°38′,
所以,这两个角分别是40°18′,27°38′.
B卷
一、1.(1)2 200 (2)2.1 210 如下图:(1)、(2):
点拨:画图时要尽量精确,量出图上距离后,利用比例尺的计算公式,算出实际距离.
2.按要求画图如下:
分析:因为光线被反射的特点是∠AOC=∠BOC,故画时仿照题目给出的图形画,只改变角度的大小,即画∠AOC=∠BOC=50°.
二、
3.能 解:设“模板”角度为a,假设可由k个a角与t个180°角画出1°的角来,
即k,t满足等式:ka+180°t=1°(*),则总是等价于求不定方程(*)的解.
当a=19°时,由于(19,180)=1,
由不定方程的知识知,(*)式有解,且k=19,t=-2,
即为其中的一解,即用模板连续画出19个19°的角,得到361°,去掉360°的角,
即得1°的角.
4.∠CDE=90° 分析:DE、DC分别∠BDA′和∠ADA′的平分线.
由折叠过程知∠BDE=∠A′DE,∠ADC=∠A′DC.
∴∠CDE=∠CDA′+∠EDA′=∠ADA′+∠BDA′
=(∠ADA′+∠BDA′)=×180°=90°.
三、
5.∠1+∠2+∠3+…+∠9=405°
分析:∵∠3=∠5=∠7=45°,∠1+∠9=∠2+∠6=∠4+∠8=2∠7=90°.
∴∠1+∠2+…+∠9=(∠1+∠9)+(∠2+∠6)+(∠4+∠8)+(∠3+∠5+∠7)
=3×90°+3×45°=405°.
点拨:除∠3=∠5=∠7外,其他度数均不知道,注意到图形的对称性,沿BD对折,图形能够重合,得到∠1+∠9=∠2+∠6=∠4+∠8=90°.
6.共有四次时针与分针所夹的角为60°,分别为2点整;2点21分;3点5分;3点27分.
分析:(Ⅰ)第一次正好为2点整,如下图(1)所示:
(Ⅱ)第二次如图(2),设为2点x分时,时针与分针的夹角为60°,
则分针转动(6x)°,而时针转动()°,且分针追及时针共120°,
所以6x-=120,x==21.即2点21分时,时针与分针的夹角为60°.
(Ⅲ)第三次如图(3)所示,设3点y分,
由于在正3点时,时针与分针的夹角为90°,
而分针转动(从正3点开始计算)(6y)°,时针转动()°,
且分针追及时针的角度为30°,
于是有6y-=30,y==5,
即3点5分时,时针与分针的夹角为60°.
(Ⅳ)第四次,如图(4)所示,设为3点z分.
同理,在正3点时,时针与分针的夹角为90°,
而分针转动(从3点开始计算)(6z)°,时针转动()°,
且分针追及时针的角度为60°+90°=150°,
于是有6z-=150,z==27,
即3点27分时,时针与分针的夹角为60°.
四、
7.B 分析:分针转一周的,时针转一个格的,
时针与分针的夹角是30°+30°+30°×=82.5°.
点拨:考查求钟表上时针与分针的夹角.
8.60 分析:在弯成钢架之前,存在以A为顶点的平角,截面的缺口是多少度,变成钢架后的角就比平角小多少度.
解:180°-120°=60°,故在角钢上截去的缺口是60°. ( http: / / )
- 9 -
A卷 基础知识达标
(45分钟 100分)
一、选择题(每题4分,共32分)
1.如图1所示,从点O出发的5条射线,可以组成的角的个数是( ).
A.4 B.6 C.8 D.10
2.下列语句,正确的是( ).
A.直线可表示一个平角; B.平角的两边向左右无限延伸;
C.延长线段AB至点C,则∠ACB=180°;
D.在一条直线上顺次取三点A、B、C,则∠ABC=180° (1)
3.射线OA和射线OB是一个角的两边,这个角可记为( ).
A.∠AOB B.∠BAO C.∠OBA D.∠OAB
4.角度是( )进制.
A.二 B.八 C.十 D.六十
5.0.25°等于( )分.
A.60 B.15 C.90 D.360
6.下面语句中,正确的是( ).
A.两个互补的角是平角; B.一条直线就是一个平角;
C.两条直线相交,形成4个小于平角的角;
D.点A、B分别在∠O的两条边上,则它们到点O的距离越大,∠O也越大.
7.钟表在5点30分时,它的时针和分针所成的锐角是( ).
A.15° B.70° C.30° D.90°
8.学校、电影院、公园的平面图上的标点分别是A、B、C,电影院在学校的正东方向,公园在学校的南偏西25°方向,那么平面图上的∠CAB等于( ).
A.115° B.25° C.155° D.65°
二、填空题(每题3分,共21分)
9.钟表的时间为2时整,时针与分针所夹的角是_____度.
10.如图2所示,图中共有______条线段,______个小于平角的角.
(2) (3) (4) (5)
11.如图3中以A为顶点的角的个数,与直线L上线段的条数_______(填“相等”或“不相等”).
12.如图4中∠AOB的两边与直线L_______(填“相交”或“不相交”).
13.43°29′47″+36°30′13″=__________,23°30′=_______°,13.6°=_______°________′.
14.如图5所示,∠BAD=_______+______,∠AOC=______+______,我们也把∠AOC叫做________角.
15.时钟的分针1小时转_______度,时针1小时转______度;时钟的分针1分钟转_______度,时针1分钟转________度.
三、计算题:(每题5分,共15分).
16.36.32°=_______°_______′________″.
17.52°25′12″=_________°.
18.180°-(22°30′42″+67°20′20″)=______=_____°_____′______″.
四、解答题(每题8分,共40分)
19.若时钟由2点30分走到2点55分,问时针、分针各转过多大的角度?
20.在8点与9点之间,分针与时针重合的时刻是几点几分?
21.试用等腰三角板和一个30°,60°的三角板画出15°,135°的角.
22.两个角的和为67°56′,差是12°40′,求这两个角.
B卷 发散创新应用
(45分钟 100分)
一、综合题(1题20分,2题10分,共30分)
1.用1:100的比例尺画图,并填空:
(1)如图①,小王从O点向北偏西60°走了200m,到达A处,小李从O点向南偏西60°走了200m,到达B处,用刻度尺量得AB=______cm,AB的实际距离=_____m.
(2)如图②,小张从O点向东北方向走了200m到达M点,又向正南方向走了300m到达N点,用刻度尺量得ON=_______cm,ON的实际距离=______m.
2.如图所示,是一束光线照射到镜面上一点O之后被反射的情况,MN表示镜面,OC⊥MN,光线被反射的特点是∠AOC=∠BOC.请画出当∠AOC=50°时的入射光线和反射光线.
二、应用题(每题15分,共30分)
3.现有一个19°的“模板”(如图3-3-8所示),请你设计一种办法,只用这个“模板”和铅笔在纸上画出1°的角来.
4.取一张长方形纸片,如图3-3-9①所示,折叠一个角,记顶点A落下的位置为A′,折痕为CD,如图3-3-9②所示再折叠另一个角,使DB沿DA′方向落下,折痕为DE,试判断∠CDE的大小,并说明理由.
三、创新题(每题15分,共30分)
5.如图3-3-10所示,是一个3×3的正方形ABCD,求∠1+∠2+∠3+…+∠9的和.
6.钟面从2点到4点有几次时针与分针夹角成60°角?分别是几点几分?
四、中考题:(每题5分,共10分)
7.钟表上12时15分钟时,时针和分针的夹角为( ).
A.90° B.82.5° C.67.5° D.60°
8.如图所示,要把角钢①弯成120°的钢架②,则在角钢①上截去的缺口是_______度.
答案:
A卷
一、
1.D 分析:假设图中所成的角以OA为始边,那么OB、OC、OD、OE可以成为角的终边,这样可以构成∠AOB、∠AOC、∠AOD和∠AOE;以OC为始边,则可构成∠BOC、∠BOD和∠BOE;以OC为始边,则可构成∠COD和∠COE;以OD为始边,则可构成∠DOE,这样共可组成角的个数为10个. 点拨:不要重复数,也不要漏掉.
2.D 分析:角的构成有三要素,故A项中只有边而没有顶点,不符合题意.角的两边都是射线,只能向一方延伸,而不能向左右延伸,故B项错误.延长线段AB至点C,则AC边与BC边重合,∠ACB=0°,故不可能为180°.D项中A、B、C三点在一条直线上,且A、C两点在B点的两边,构成一个平角,故D项符合题意.
3.A 分析:角的表示通常为:用三个大写的英文字母和“∠”表示,中间字母是角的顶点,其他两个字母分别是表示角的两边上的点.当一个点作为多个角的顶点时,常用此种方法表示.因此,点O一定是中间的字母,故选A.
4.D 点拨:角度制常以度、分、秒为单位.而度、分、秒之间换算单位是60.
5.B 分析:一个周角为360°,把1度的角60等分,每一份叫做1分的角,
故0.25°=0.25×60分=15分.
6.C 分析:两个互补的角是两个角,平角是一个角;
两直线相交,确实形成4个小于平角的角.
7.A 分析:钟表时针旋转一周为360°,共12时辰,
则每邻近两个时辰所夹的角为360°÷12=30°,
当钟表为5时30分钟时,时针正好位于5时和6时中间,
而分针正指6时,此时时针和分针所夹角为:30°÷2=15°,
故A为正确答案.
8.A 分析:如右图,一平面内以学校A为中点,
则正东与正南所成的角为360°÷=90°,
而公园C在学校A的南偏西25°,
则∠CAB=90°+25°=115°,
故A符合题意.
二、
9.60 分析:钟表盘上每邻近两个时辰所夹的角为360°÷12=30°,
当钟表为2时整时,时针指向“2”,
而分针指向“12”,那么时针和分针所夹角为2×30°=60°.
10.7 8 点拨:关键是与点A有关的线段与小于平角的角的数目.
11.相等 分析:每一个以A为顶点的角,其两边都在直线L上截得一条线段.
12.相交 分析:角的两边是射线,直线L更是向两边无限伸展的.
13.80° 23.5° 13 36
分析:把一个周角360等分,每一份都是1度的角,记作1°;
把1度的角60等分,每一份叫做1分的角,记作1′;
把1分的角60等分,每一份叫做1秒的角,记作1″,
故43°29′47″+36°30′13″=79°59′60″=79°60′=80°,
23°30′=23.5°,13.6°=13°+0.6×60′=13°36′.
14.∠BAC ∠CAD ∠AOD ∠DOC 平
分析:射线OC是以∠BAD中A为顶点的一条射线,它把∠BAD分成了两个角:∠BAC∠和∠CAD.同理,射线OD也把∠AOC分成了两个角:∠AOD与∠DOC.∠AOC的两边OA与OC均在一条直线上,故∠AOC=180°.
15.360 30 6 0.5
分析:时钟的分针1小时转一周为360°,
则分针1分钟转的度数为360°÷60=6°,时针1小时(60分钟)转30°,
则1分钟转的度数=30°÷60=0.5°.
三、
16.36°19′12″
点拨:把度化为度、分、秒,必须先把不足1度的化为分,再把不足1分的化为秒,也就是把角的度量单位由大小的过程,每步要乘60′和60″.
17.52.42° 点拨:把度、分、秒化为度,必须把秒化为分,然后再加上原有的分,再化为度,也就是把角的度量单位由小化大的过程,每步要乘()°或()′.
18.180°-89°51′2″ 90°8′58″
点拨:角的加减运算,必须把度、分、秒分别相加减,
进位时,60″=1′,60′=1°,借位时,1°=60′,1′=60″.
四、
19.150° 12.5°
解:分针所走度数:×(55-30)=6°×25=150°,
时针所走度数:×(55-30)==12.5°.
20.分针与时针重合的时刻是8点43分
分析:在8点整时,时针与分针成240°,
设分针与时针重合是在8点x分.
因为分针每分钟转动一小格,即6°,所以分针共转动(6x)°,
而时针转动的速度只有分针的,即()°,
依题意有:6x-=240,
所以x==43分.即分针与时针重合的时刻是在8点43分.
21.分析:先用等腰三角板画出一个45°的角∠AOB,以O为顶点,OB为始边,
用30°,60°的三角板作出∠BOC=60°,则∠AOC=15°,
如上图(1),先作出一个45°的角,∠AOB=45°,反向延长OA至C,则∠BOC=135°.
如上图(2).
22.这两个角分别是40°18′,27°38′
分析:设这两个角分别为x,y,则
所以x==40°18′,y=67°56′-40°18′=27°38′,
所以,这两个角分别是40°18′,27°38′.
B卷
一、1.(1)2 200 (2)2.1 210 如下图:(1)、(2):
点拨:画图时要尽量精确,量出图上距离后,利用比例尺的计算公式,算出实际距离.
2.按要求画图如下:
分析:因为光线被反射的特点是∠AOC=∠BOC,故画时仿照题目给出的图形画,只改变角度的大小,即画∠AOC=∠BOC=50°.
二、
3.能 解:设“模板”角度为a,假设可由k个a角与t个180°角画出1°的角来,
即k,t满足等式:ka+180°t=1°(*),则总是等价于求不定方程(*)的解.
当a=19°时,由于(19,180)=1,
由不定方程的知识知,(*)式有解,且k=19,t=-2,
即为其中的一解,即用模板连续画出19个19°的角,得到361°,去掉360°的角,
即得1°的角.
4.∠CDE=90° 分析:DE、DC分别∠BDA′和∠ADA′的平分线.
由折叠过程知∠BDE=∠A′DE,∠ADC=∠A′DC.
∴∠CDE=∠CDA′+∠EDA′=∠ADA′+∠BDA′
=(∠ADA′+∠BDA′)=×180°=90°.
三、
5.∠1+∠2+∠3+…+∠9=405°
分析:∵∠3=∠5=∠7=45°,∠1+∠9=∠2+∠6=∠4+∠8=2∠7=90°.
∴∠1+∠2+…+∠9=(∠1+∠9)+(∠2+∠6)+(∠4+∠8)+(∠3+∠5+∠7)
=3×90°+3×45°=405°.
点拨:除∠3=∠5=∠7外,其他度数均不知道,注意到图形的对称性,沿BD对折,图形能够重合,得到∠1+∠9=∠2+∠6=∠4+∠8=90°.
6.共有四次时针与分针所夹的角为60°,分别为2点整;2点21分;3点5分;3点27分.
分析:(Ⅰ)第一次正好为2点整,如下图(1)所示:
(Ⅱ)第二次如图(2),设为2点x分时,时针与分针的夹角为60°,
则分针转动(6x)°,而时针转动()°,且分针追及时针共120°,
所以6x-=120,x==21.即2点21分时,时针与分针的夹角为60°.
(Ⅲ)第三次如图(3)所示,设3点y分,
由于在正3点时,时针与分针的夹角为90°,
而分针转动(从正3点开始计算)(6y)°,时针转动()°,
且分针追及时针的角度为30°,
于是有6y-=30,y==5,
即3点5分时,时针与分针的夹角为60°.
(Ⅳ)第四次,如图(4)所示,设为3点z分.
同理,在正3点时,时针与分针的夹角为90°,
而分针转动(从3点开始计算)(6z)°,时针转动()°,
且分针追及时针的角度为60°+90°=150°,
于是有6z-=150,z==27,
即3点27分时,时针与分针的夹角为60°.
四、
7.B 分析:分针转一周的,时针转一个格的,
时针与分针的夹角是30°+30°+30°×=82.5°.
点拨:考查求钟表上时针与分针的夹角.
8.60 分析:在弯成钢架之前,存在以A为顶点的平角,截面的缺口是多少度,变成钢架后的角就比平角小多少度.
解:180°-120°=60°,故在角钢上截去的缺口是60°. ( http: / / )
- 9 -
