2022-2023学年人教版九年级数学上册 22.3 实际问题与二次函数同步提高训练(含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册 22.3 实际问题与二次函数同步提高训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 731.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 20:04:35 | ||
图片预览

文档简介
22.3 实际问题与二次函数同步提高训练
一、单选题
1.当axa+1时,函数y=-2x+1的最小值为4,则a的值为( )
A. -2 B. 4 C. 4或3 D. -2或3
2.某畅销书的售价为每本30元,每星期可卖出200本,经调研,如果调整书籍的售价,每降价2元,每星期可多卖出40本,设每件商品降价x元后,每星期售出此畅销书的总销售额为y元,则y与x之间的函数关系为( )
A. B.
C. D.
3.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
4.已知y=ax2+bx+3(a≠0)的对称轴为直线x=2,与x轴的其中一个交点为(1,0),该函数在1≤x≤4的取值范围,下列说法正确的是( )
A. 有最小值0,有最大值3 B. 有最小值-1,有最大值3
C. 有最小值-3,有最大值4 D. 有最小值-1,有最大值4
5.果农计划对果园加大种植密度,据测算,果园的总产量个与增种果树的棵数棵间的函数关系式为,要使总产量在60320个以上,需要增加果树的棵数范围是
A. B.或 C. D.或
6.为响应国家的惠民政策,某种口罩原价每箱100元,经过两次降价后每箱81元.设平均每次降价的百分率都为x,则x满足( )
A.81(1+2x)= 100 B.100(1-2x)=81
C.81(1+x)=100 D.100(1-x)=81
7.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m-n的最大值等于( )
A. B. 4 C. - D. -
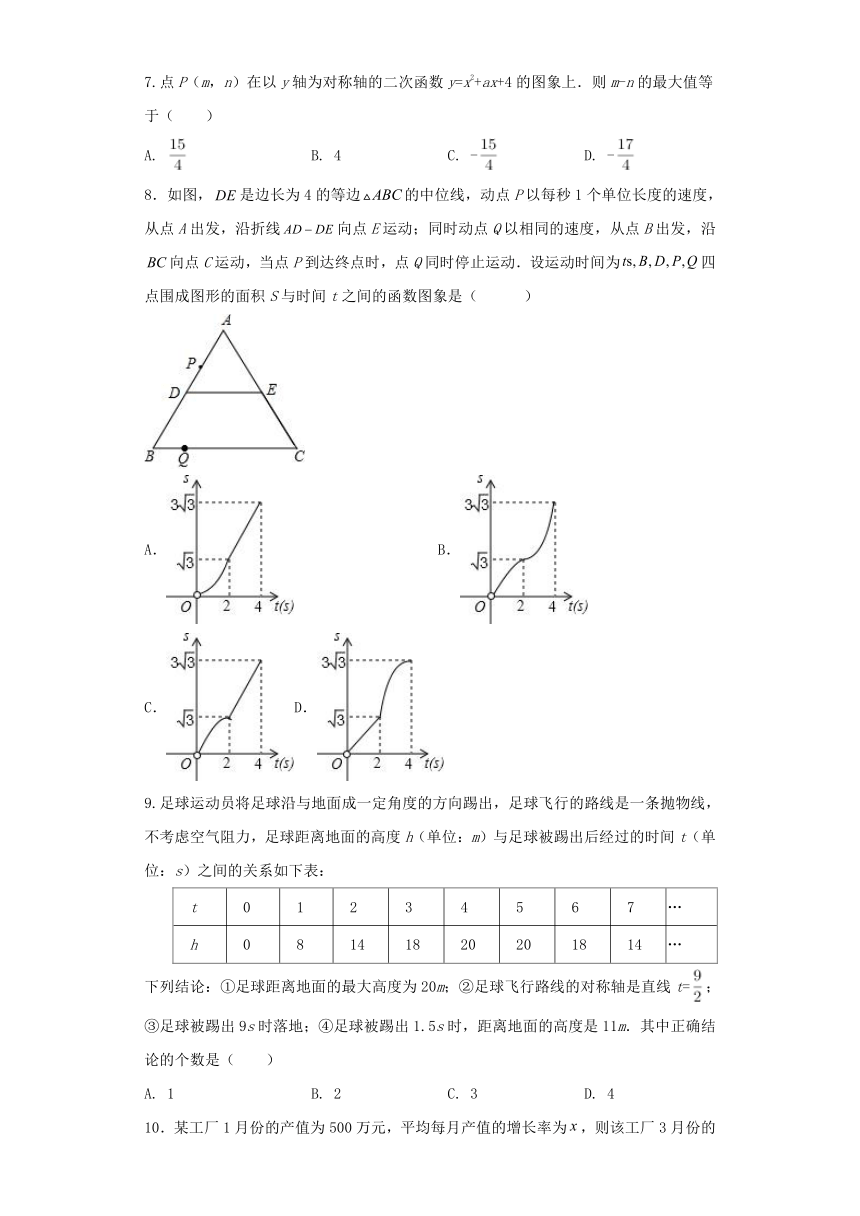
8.如图,是边长为4的等边的中位线,动点P以每秒1个单位长度的速度,从点A出发,沿折线向点E运动;同时动点Q以相同的速度,从点B出发,沿向点C运动,当点P到达终点时,点Q同时停止运动.设运动时间为四点围成图形的面积S与时间t之间的函数图象是( )
A. B.
C. D.
9.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
10.某工厂1月份的产值为500万元,平均每月产值的增长率为,则该工厂3月份的产值与之间的函数解析式为( )
A. B. C. D.
二、填空题
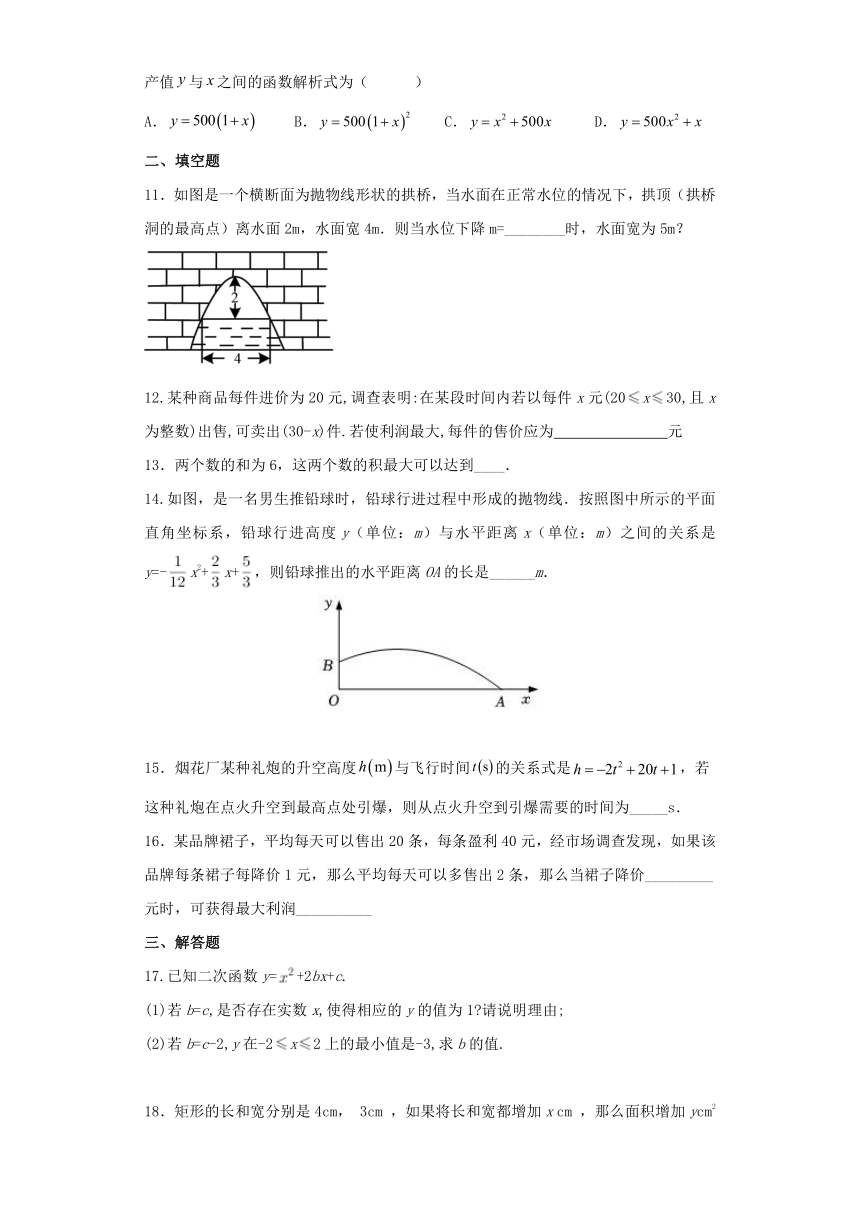
11.如图是一个横断面为抛物线形状的拱桥,当水面在正常水位的情况下,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.则当水位下降m=________时,水面宽为5m?
12.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20x30,且x为整数)出售,可卖出(30-x)件.若使利润最大,每件的售价应为 元
13.两个数的和为6,这两个数的积最大可以达到____.
14.如图,是一名男生推铅球时,铅球行进过程中形成的抛物线.按照图中所示的平面直角坐标系,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=-x2+x+,则铅球推出的水平距离OA的长是______m.
15.烟花厂某种礼炮的升空高度与飞行时间的关系式是,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为_____s.
16.某品牌裙子,平均每天可以售出20条,每条盈利40元,经市场调查发现,如果该品牌每条裙子每降价1元,那么平均每天可以多售出2条,那么当裙子降价_________元时,可获得最大利润__________
三、解答题
17.已知二次函数y=+2bx+c.
(1)若b=c,是否存在实数x,使得相应的y的值为1 请说明理由;
(2)若b=c-2,y在-2x2上的最小值是-3,求b的值.
18.矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm2
(1)求y与x之间的关系式.
(2)求当边长增加多少时,面积增加8 cm2 .
19.“国庆节期间”某商场销售一款商品,每件的成本是元.销售期间发现:销售单价是元时,每天销售量是件,而销售单价每降低元,每天就可多售出件.但要求销售单价不得低于成本.设当销售单价为元时,每天销售利润为元.
(1)求与之间的函数表达式.
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果每天的销售利润不低于元,那么每天的总成本至少需要 元.
20.一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12.用这块材料剪出一个矩形CDEF,其中,点D,E,F分别在BC,AB,AC上.要使剪出的矩形CDEF的面积最大,点E应选在何处?
21.为了落实国务院的指示精神,某地方政府出台了一系列“精准扶贫”优惠政策,使贫困户收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量(千克)与销售价(元/千克)有如下关系:.设这种产品每天的销售利润为元.
(1)求与之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克30元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
参考答案
1.D 2.D 3.C 4.B 5.A 6.D 7.C 8.A 9.C 10.B
11.
12.25
13.9
14.10
15.5
16. 15 1250
17.解:(1)存在满足条件的实数x.理由如下:
若b=c,由y=1得+2bx+b=1,
+2bx+b-1=0,
=-4b+4=+3>0,即关于x一元二次方程+2bx+b-1=0有两个不相等的实数解,
存在两个实数x,使得相应的y=1.
(2)由b=c-2得c=b+2,
则抛物线解析式可化为y=+2bx+b+2,其对称轴为直线x=-b,开口向上;
当-b-2时,
∵y在-2x2上的最小值是-3,
∴在x=-2时,y取最小值为-3,
此时-3=+2b(-2)+b+2,
解得b=3;
当-b2时,
∵y在-2x2上的最小值是-3,
∴在x=2时,y取最小值为-3,
此时-3=+22b+b+2,
解得b=-,不合题意,舍去;
当-2<-b<2时,
∵y在-2x2上的最小值是-3,
∴=-3,
化简得-b-5= 0,
解得=(不合题意,舍去),= .
综上所述,b=3或.
18.(1)y=x2+7x;(2)边长增加1cm时,面积增加8 cm2.
【详解】
解:(1)由题意可得:(4+x)(3+x)-3×4=y,
化简得:y=x2+7x;
(2)把y=8代入解析式y=x2+7x中得:x2+7x-8=0,
解之得:x1=1,x2=-8(舍去).
∴当边长增加1cm时,面积增加8cm2
19.(1)
(2)元,最大利润元
(3)
20.解:(1)①当12≤x≤20时,设y=kx+b.代(12,2000),(20,400),
得,
解得,
∴y=-200x+4400,
②当20<x≤24时,y=400.
综上,y与x之间的函数解析式为y=;
(2)①当12≤x≤20时,
W=(x-12)y
=(x-12)(-200x+4400)
=-200(x-17)2+5000,
当x=17时,W的最大值为5000;
②当20<x≤24时,
W=(x-12)y
=400x-4800.
当x=24时,W的最大值为4800.
∴这一天销售羊肚菌获得的最大利润为5000元.
21.(1)w=-2x2+120x-1600
(2)销售价定为每千克30元时,每天销售利润最大,最大销售利润200元
(3)每千克25
一、单选题
1.当axa+1时,函数y=-2x+1的最小值为4,则a的值为( )
A. -2 B. 4 C. 4或3 D. -2或3
2.某畅销书的售价为每本30元,每星期可卖出200本,经调研,如果调整书籍的售价,每降价2元,每星期可多卖出40本,设每件商品降价x元后,每星期售出此畅销书的总销售额为y元,则y与x之间的函数关系为( )
A. B.
C. D.
3.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
4.已知y=ax2+bx+3(a≠0)的对称轴为直线x=2,与x轴的其中一个交点为(1,0),该函数在1≤x≤4的取值范围,下列说法正确的是( )
A. 有最小值0,有最大值3 B. 有最小值-1,有最大值3
C. 有最小值-3,有最大值4 D. 有最小值-1,有最大值4
5.果农计划对果园加大种植密度,据测算,果园的总产量个与增种果树的棵数棵间的函数关系式为,要使总产量在60320个以上,需要增加果树的棵数范围是
A. B.或 C. D.或
6.为响应国家的惠民政策,某种口罩原价每箱100元,经过两次降价后每箱81元.设平均每次降价的百分率都为x,则x满足( )
A.81(1+2x)= 100 B.100(1-2x)=81
C.81(1+x)=100 D.100(1-x)=81
7.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m-n的最大值等于( )
A. B. 4 C. - D. -
8.如图,是边长为4的等边的中位线,动点P以每秒1个单位长度的速度,从点A出发,沿折线向点E运动;同时动点Q以相同的速度,从点B出发,沿向点C运动,当点P到达终点时,点Q同时停止运动.设运动时间为四点围成图形的面积S与时间t之间的函数图象是( )
A. B.
C. D.
9.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
10.某工厂1月份的产值为500万元,平均每月产值的增长率为,则该工厂3月份的产值与之间的函数解析式为( )
A. B. C. D.
二、填空题
11.如图是一个横断面为抛物线形状的拱桥,当水面在正常水位的情况下,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.则当水位下降m=________时,水面宽为5m?
12.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20x30,且x为整数)出售,可卖出(30-x)件.若使利润最大,每件的售价应为 元
13.两个数的和为6,这两个数的积最大可以达到____.
14.如图,是一名男生推铅球时,铅球行进过程中形成的抛物线.按照图中所示的平面直角坐标系,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=-x2+x+,则铅球推出的水平距离OA的长是______m.
15.烟花厂某种礼炮的升空高度与飞行时间的关系式是,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为_____s.
16.某品牌裙子,平均每天可以售出20条,每条盈利40元,经市场调查发现,如果该品牌每条裙子每降价1元,那么平均每天可以多售出2条,那么当裙子降价_________元时,可获得最大利润__________
三、解答题
17.已知二次函数y=+2bx+c.
(1)若b=c,是否存在实数x,使得相应的y的值为1 请说明理由;
(2)若b=c-2,y在-2x2上的最小值是-3,求b的值.
18.矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm2
(1)求y与x之间的关系式.
(2)求当边长增加多少时,面积增加8 cm2 .
19.“国庆节期间”某商场销售一款商品,每件的成本是元.销售期间发现:销售单价是元时,每天销售量是件,而销售单价每降低元,每天就可多售出件.但要求销售单价不得低于成本.设当销售单价为元时,每天销售利润为元.
(1)求与之间的函数表达式.
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果每天的销售利润不低于元,那么每天的总成本至少需要 元.
20.一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12.用这块材料剪出一个矩形CDEF,其中,点D,E,F分别在BC,AB,AC上.要使剪出的矩形CDEF的面积最大,点E应选在何处?
21.为了落实国务院的指示精神,某地方政府出台了一系列“精准扶贫”优惠政策,使贫困户收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量(千克)与销售价(元/千克)有如下关系:.设这种产品每天的销售利润为元.
(1)求与之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克30元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
参考答案
1.D 2.D 3.C 4.B 5.A 6.D 7.C 8.A 9.C 10.B
11.
12.25
13.9
14.10
15.5
16. 15 1250
17.解:(1)存在满足条件的实数x.理由如下:
若b=c,由y=1得+2bx+b=1,
+2bx+b-1=0,
=-4b+4=+3>0,即关于x一元二次方程+2bx+b-1=0有两个不相等的实数解,
存在两个实数x,使得相应的y=1.
(2)由b=c-2得c=b+2,
则抛物线解析式可化为y=+2bx+b+2,其对称轴为直线x=-b,开口向上;
当-b-2时,
∵y在-2x2上的最小值是-3,
∴在x=-2时,y取最小值为-3,
此时-3=+2b(-2)+b+2,
解得b=3;
当-b2时,
∵y在-2x2上的最小值是-3,
∴在x=2时,y取最小值为-3,
此时-3=+22b+b+2,
解得b=-,不合题意,舍去;
当-2<-b<2时,
∵y在-2x2上的最小值是-3,
∴=-3,
化简得-b-5= 0,
解得=(不合题意,舍去),= .
综上所述,b=3或.
18.(1)y=x2+7x;(2)边长增加1cm时,面积增加8 cm2.
【详解】
解:(1)由题意可得:(4+x)(3+x)-3×4=y,
化简得:y=x2+7x;
(2)把y=8代入解析式y=x2+7x中得:x2+7x-8=0,
解之得:x1=1,x2=-8(舍去).
∴当边长增加1cm时,面积增加8cm2
19.(1)
(2)元,最大利润元
(3)
20.解:(1)①当12≤x≤20时,设y=kx+b.代(12,2000),(20,400),
得,
解得,
∴y=-200x+4400,
②当20<x≤24时,y=400.
综上,y与x之间的函数解析式为y=;
(2)①当12≤x≤20时,
W=(x-12)y
=(x-12)(-200x+4400)
=-200(x-17)2+5000,
当x=17时,W的最大值为5000;
②当20<x≤24时,
W=(x-12)y
=400x-4800.
当x=24时,W的最大值为4800.
∴这一天销售羊肚菌获得的最大利润为5000元.
21.(1)w=-2x2+120x-1600
(2)销售价定为每千克30元时,每天销售利润最大,最大销售利润200元
(3)每千克25
同课章节目录
