2022-2023学年人教版九年级数学上册22.3 实际问题与二次函数--图形问题专题训练 (含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册22.3 实际问题与二次函数--图形问题专题训练 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 570.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 00:00:00 | ||
图片预览


文档简介
22.3 实际问题与二次函数--图形问题专题训练
一、单选题
1.如图,要把长为、宽为的长方形花坛四周扩展相同的宽度,得到面积为的新长方形花坛,则的值为( )
A. B. C. D.
2.小明以二次函数的图象为灵感为某葡萄酒大赛设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高CE为( )
A.12 B.11 C.6 D.3
3. 如图,假设篱笆(虚线部分)的长度为16 m,则所围成矩形ABCD的最大面积是( )
A.60 m2 B.63 m2 C.64 m2 D.66 m2
4.用6m长的铝合金型材做一个形状如图所示的矩形窗框.若窗框的面积为,则窗框AB的长为( )
A.1m B.1.5m C.1.6m D.1.8m
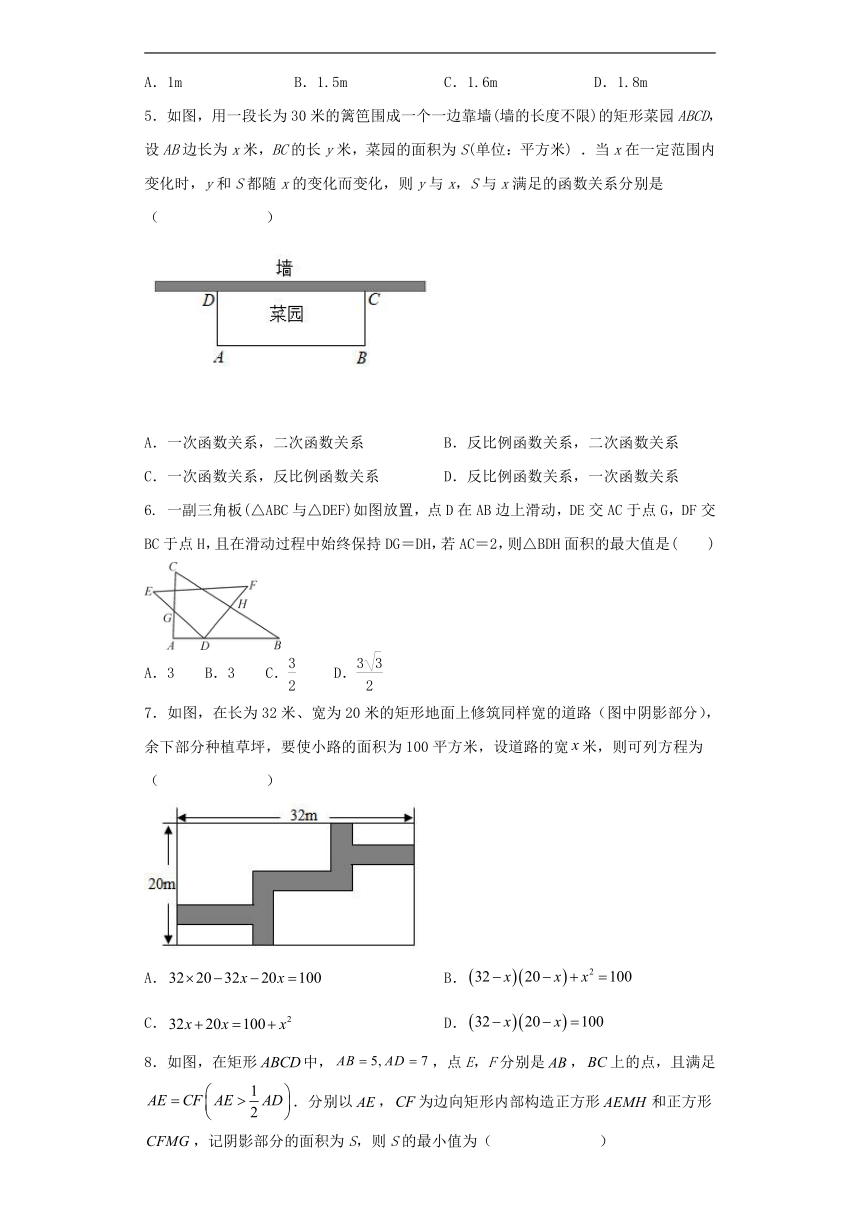
5.如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边长为x米,BC的长y米,菜园的面积为S(单位:平方米) .当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
6. 一副三角板(△ABC与△DEF)如图放置,点D在AB边上滑动,DE交AC于点G,DF交BC于点H,且在滑动过程中始终保持DG=DH,若AC=2,则△BDH面积的最大值是( )
A.3 B.3 C. D.
7.如图,在长为32米、宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使小路的面积为100平方米,设道路的宽米,则可列方程为( )
A. B.
C. D.
8.如图,在矩形中,,点E,F分别是,上的点,且满足.分别以,为边向矩形内部构造正方形和正方形,记阴影部分的面积为S,则S的最小值为( )
A.9 B.10.5 C.12 D.15
9. 如图,△ABC是直角三角形,∠A=90°,AB=8 cm,AC=6 cm,点P从点A出发,沿AB方向以2 cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1 cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则△PAQ的最大面积是( )
A.8 cm2 B.9 cm2 C.16 cm2 D.18 cm2
10.如图,某学校有一块长32米.宽20米的长方形试验田,为了便于管理,现要在中间开辟两条等宽的弯曲小道,要使种植面积为600平方米.设小道的宽为x米,根据题意可列方程为( )
A. B.
C. D.
二、填空题
11. 如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为_______.
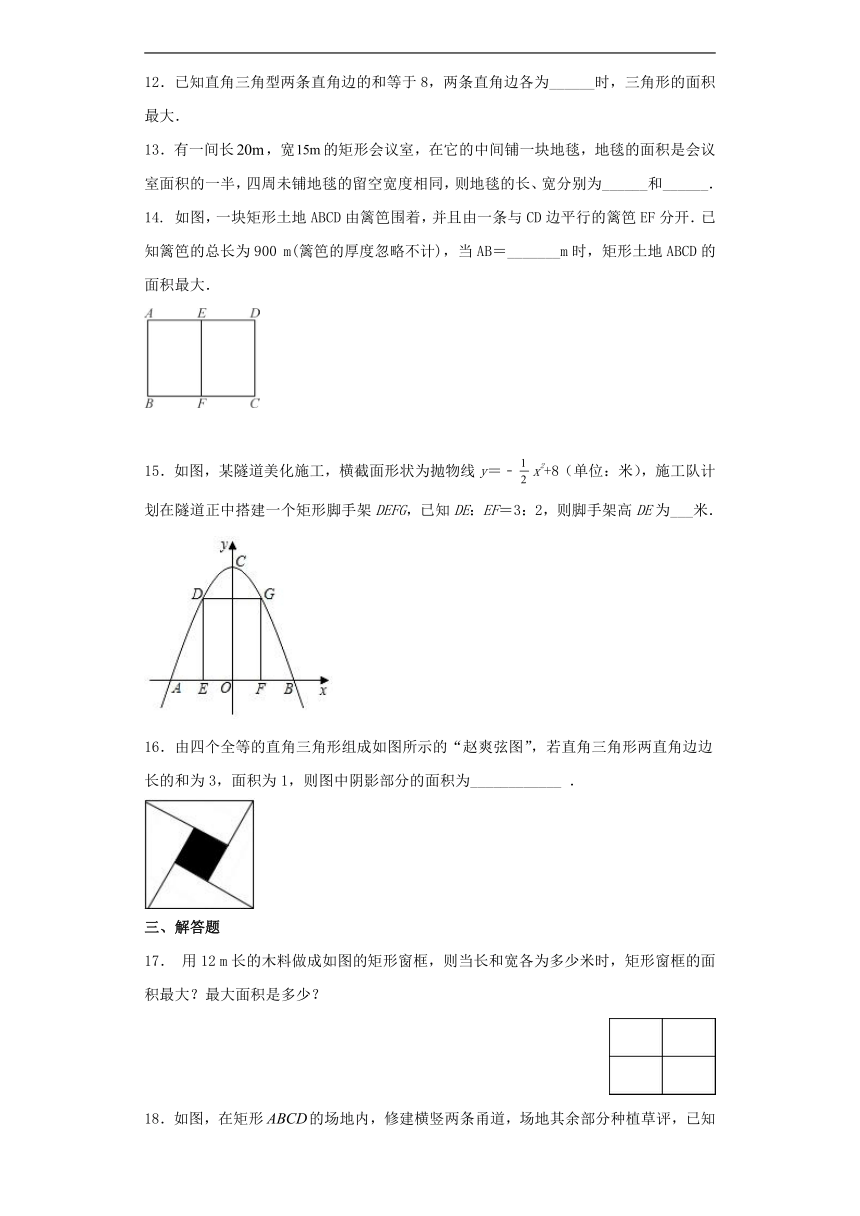
12.已知直角三角型两条直角边的和等于8,两条直角边各为______时,三角形的面积最大.
13.有一间长,宽的矩形会议室,在它的中间铺一块地毯,地毯的面积是会议室面积的一半,四周未铺地毯的留空宽度相同,则地毯的长、宽分别为______和______.
14. 如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900 m(篱笆的厚度忽略不计),当AB=_______m时,矩形土地ABCD的面积最大.
15.如图,某隧道美化施工,横截面形状为抛物线y=﹣x2+8(单位:米),施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,则脚手架高DE为___米.
16.由四个全等的直角三角形组成如图所示的“赵爽弦图”,若直角三角形两直角边边长的和为3,面积为1,则图中阴影部分的面积为____________ .
三、解答题
17. 用12 m长的木料做成如图的矩形窗框,则当长和宽各为多少米时,矩形窗框的面积最大?最大面积是多少?
18.如图,在矩形的场地内,修建横竖两条甬道,场地其余部分种植草评,已知竖向甬道的宽度是横向甬道宽度的2倍,米,米,设横向甬道的宽度为x米,草坪面积为y米2.
(1)请写出y与x之间的函数关系式;(不必写出自变量的取值范围)
(2)若草坪面积为270米2,请求出横向甬道的宽度.
19.如图,一长方形草坪长50米,宽30米,在草坪上有两条互相垂直且宽度相等的长方形小路(阴影部分),非阴影部分的面积是924米.
(1)求小路的宽度;
(2)每平方米小路的建设费用为200元,求修建两条小路的总费用.
20.用长24 m的篱笆围成如图中间有一道篱笆的矩形花圃,墙长9 m,设垂直于墙的长度为x m,花圃的面积为S m2.
(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)当x为多少时,花圃的面积最大,最大面积是多少?
21.如图所示的是一座拱桥,桥洞的拱形是抛物线的形状,当水面宽AB为12米时,桥洞顶部离水面4米,若水面上涨1米,求此时水面的宽.
22. 某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50 m.设饲养室长为x(m),占地面积为y(m2).
(1)如图①,问饲养室长x为多少时,占地面积y最大?
(2)如图②,现要求在图中所示位置留2 m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2 m就行了.”请你通过计算,判断小敏的说法是否正确.
参考答案
1-5BCCDB 6-10CCBCC
11. 10米
12.4 4
13. 15m 10m
14.150
15.6
16.1
17. 解:设长为x m,则宽为·(12-3x)=(4-x)m,S=x(4-x)=-x2+4x=-(x-2)2+4,∴当x=2 m时,长宽均为2 m,窗框有最大面积为4 m2
18.(1)
(2)横甬道的宽度为
19.(1)小路的宽为8米;
(2)修建两条小路的总费用为115200元.
20. 解:(1)由题意得S=x(24-3x)=-3x2+24x(5≤x<8)
(2)S=-3(x-4)2+48.∵5≤x<8在对称轴x=4的右侧,此时S随x的增大而减小,∴当x=5时,S最大=45(m2).答:当x=5时,花圃的面积最大为45 m2
21.6米
【详解】
解:如图,以抛物线的顶点为原点,建立平面直角坐标系.
由题意可知抛物线过点(6,-4)
设抛物线的函数表达式为:
把(6,-4)代入,可得
则抛物线的函数表达式为:
当水面上涨1米,水面所在的位置为直线
令,则,解得:
∴此时水面的宽为:6米.
22. 解:(1)∵y=x·=-(x-25)2+,∴当x=25时,占地面积最大,即当饲养室长x为25 m时,占地面积y最大
(2)∵y=x·=-(x-26)2+338,∴当x=26时,占地面积最大,即当饲养室长x为26 m时,占地面积y最大;∵26-25=1≠2,∴小敏的说法不正确
一、单选题
1.如图,要把长为、宽为的长方形花坛四周扩展相同的宽度,得到面积为的新长方形花坛,则的值为( )
A. B. C. D.
2.小明以二次函数的图象为灵感为某葡萄酒大赛设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高CE为( )
A.12 B.11 C.6 D.3
3. 如图,假设篱笆(虚线部分)的长度为16 m,则所围成矩形ABCD的最大面积是( )
A.60 m2 B.63 m2 C.64 m2 D.66 m2
4.用6m长的铝合金型材做一个形状如图所示的矩形窗框.若窗框的面积为,则窗框AB的长为( )
A.1m B.1.5m C.1.6m D.1.8m
5.如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边长为x米,BC的长y米,菜园的面积为S(单位:平方米) .当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
6. 一副三角板(△ABC与△DEF)如图放置,点D在AB边上滑动,DE交AC于点G,DF交BC于点H,且在滑动过程中始终保持DG=DH,若AC=2,则△BDH面积的最大值是( )
A.3 B.3 C. D.
7.如图,在长为32米、宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使小路的面积为100平方米,设道路的宽米,则可列方程为( )
A. B.
C. D.
8.如图,在矩形中,,点E,F分别是,上的点,且满足.分别以,为边向矩形内部构造正方形和正方形,记阴影部分的面积为S,则S的最小值为( )
A.9 B.10.5 C.12 D.15
9. 如图,△ABC是直角三角形,∠A=90°,AB=8 cm,AC=6 cm,点P从点A出发,沿AB方向以2 cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1 cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则△PAQ的最大面积是( )
A.8 cm2 B.9 cm2 C.16 cm2 D.18 cm2
10.如图,某学校有一块长32米.宽20米的长方形试验田,为了便于管理,现要在中间开辟两条等宽的弯曲小道,要使种植面积为600平方米.设小道的宽为x米,根据题意可列方程为( )
A. B.
C. D.
二、填空题
11. 如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为_______.
12.已知直角三角型两条直角边的和等于8,两条直角边各为______时,三角形的面积最大.
13.有一间长,宽的矩形会议室,在它的中间铺一块地毯,地毯的面积是会议室面积的一半,四周未铺地毯的留空宽度相同,则地毯的长、宽分别为______和______.
14. 如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900 m(篱笆的厚度忽略不计),当AB=_______m时,矩形土地ABCD的面积最大.
15.如图,某隧道美化施工,横截面形状为抛物线y=﹣x2+8(单位:米),施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF=3:2,则脚手架高DE为___米.
16.由四个全等的直角三角形组成如图所示的“赵爽弦图”,若直角三角形两直角边边长的和为3,面积为1,则图中阴影部分的面积为____________ .
三、解答题
17. 用12 m长的木料做成如图的矩形窗框,则当长和宽各为多少米时,矩形窗框的面积最大?最大面积是多少?
18.如图,在矩形的场地内,修建横竖两条甬道,场地其余部分种植草评,已知竖向甬道的宽度是横向甬道宽度的2倍,米,米,设横向甬道的宽度为x米,草坪面积为y米2.
(1)请写出y与x之间的函数关系式;(不必写出自变量的取值范围)
(2)若草坪面积为270米2,请求出横向甬道的宽度.
19.如图,一长方形草坪长50米,宽30米,在草坪上有两条互相垂直且宽度相等的长方形小路(阴影部分),非阴影部分的面积是924米.
(1)求小路的宽度;
(2)每平方米小路的建设费用为200元,求修建两条小路的总费用.
20.用长24 m的篱笆围成如图中间有一道篱笆的矩形花圃,墙长9 m,设垂直于墙的长度为x m,花圃的面积为S m2.
(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)当x为多少时,花圃的面积最大,最大面积是多少?
21.如图所示的是一座拱桥,桥洞的拱形是抛物线的形状,当水面宽AB为12米时,桥洞顶部离水面4米,若水面上涨1米,求此时水面的宽.
22. 某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50 m.设饲养室长为x(m),占地面积为y(m2).
(1)如图①,问饲养室长x为多少时,占地面积y最大?
(2)如图②,现要求在图中所示位置留2 m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2 m就行了.”请你通过计算,判断小敏的说法是否正确.
参考答案
1-5BCCDB 6-10CCBCC
11. 10米
12.4 4
13. 15m 10m
14.150
15.6
16.1
17. 解:设长为x m,则宽为·(12-3x)=(4-x)m,S=x(4-x)=-x2+4x=-(x-2)2+4,∴当x=2 m时,长宽均为2 m,窗框有最大面积为4 m2
18.(1)
(2)横甬道的宽度为
19.(1)小路的宽为8米;
(2)修建两条小路的总费用为115200元.
20. 解:(1)由题意得S=x(24-3x)=-3x2+24x(5≤x<8)
(2)S=-3(x-4)2+48.∵5≤x<8在对称轴x=4的右侧,此时S随x的增大而减小,∴当x=5时,S最大=45(m2).答:当x=5时,花圃的面积最大为45 m2
21.6米
【详解】
解:如图,以抛物线的顶点为原点,建立平面直角坐标系.
由题意可知抛物线过点(6,-4)
设抛物线的函数表达式为:
把(6,-4)代入,可得
则抛物线的函数表达式为:
当水面上涨1米,水面所在的位置为直线
令,则,解得:
∴此时水面的宽为:6米.
22. 解:(1)∵y=x·=-(x-25)2+,∴当x=25时,占地面积最大,即当饲养室长x为25 m时,占地面积y最大
(2)∵y=x·=-(x-26)2+338,∴当x=26时,占地面积最大,即当饲养室长x为26 m时,占地面积y最大;∵26-25=1≠2,∴小敏的说法不正确
同课章节目录
