2022-2023学年冀教版数学九年级上册23.1平均数与加权平均数 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年冀教版数学九年级上册23.1平均数与加权平均数 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 297.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 20:08:21 | ||
图片预览



文档简介
23.1平均数与加权平均数同步练习冀教版数学九年级上册
一、单选题(共30分)
1.(本题3分)已知两组数据x,x2,…,xn和y1,y2,…,yn的平均数分别为2和-2,则x1+3y1,x2+3y2,…,xn+3yn的平均数为( )
A.-4 B.-2 C.0 D.2
2.(本题3分)已知一组数据1,0,3,-1,x,2,3的平均数是1,则这组数据的众数是( )
A.-1 B.3 C.-1和3 D.1和3
3.(本题3分)小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分 C.84.5分 D.86分
4.(本题3分)九龙坡区在中学生中开展了主题为“中华魂”的知识比赛,主要比赛项目为写作、阅读和演讲,量化评分标准比重分别为3∶2∶5,某学生写作,阅读和演讲三个项目得分分别为91分、80分、96分,则该生最后得分为( )
A.91.3 B.90 C.89 D.86.5
5.(本题3分)甲、乙、丙三种糖果售价分别为每千克6元,7元,8元,若将甲种8千克,乙种10千克,丙种3千克糖果混在一起,则售价应定为每千克( )
A.6.7元 B.6.8元 C.7.5元 D.8.6元
6.(本题3分)在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为y;同时去掉一个最高分和一个最低分,平均分为z,则( )
A.y>z>x B.x>z>y C.y>x>z D.z>y>x
7.(本题3分)2022年2月,第24届冬季奥林匹克运动会在北京举行.某校八年级(1)班在班会课开展了冬奥会知识小竞赛,10位同学在这个知识竞赛中的成绩统计结果如表所示,则这10位同学的平均成绩是( )
成绩 7 8 9 10
人数 1 4 3 2
A.8 B.8.5 C.8.6 D.9
8.(本题3分)一组数据4、5、6、a、b的平均数为5,则a、b的平均数为( )
A.4 B.5 C.8 D.10
9.(本题3分)有一组数据:2,5,5,6,7,每个数据加1后的平均数为( )
A.3 B.4 C.5 D.6
10.(本题3分)10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是( )
A. B. C. D.
二、填空题(共30分)
11.(本题3分)学校要从王静,李玉两同学中选拔一人参加运动会志愿者工作,选拔项目为普通话,体育知识和旅游知识.并将成绩依次按4∶3∶3计分. 两人的各项选拔成绩如下表所示,则最终胜出的同学是____.
普通话 体育知识 旅游知识
王静 80 90 70
李玉 90 80 70
12.(本题3分)已知数据,,, 的平均数为10,则数据,,,的平均数是______.
13.(本题3分)某水果店销售11元,18元,24元三种价格的水果,根据水果店一个月这三种水果销售量的统计图如图,可计算出该店当月销售出水果的平均价格是______元
14.(本题3分)在植树节当天,某班的四个绿化小组植树的棵数如下:10,8,9,9,则这组数据的平均数是___________.
15.(本题3分)某小组6名学生的平均身高为acm,规定超过acm的部分记为正数,不足acm的部分记为负数,他们的身高与平均身高的差值情况记录如下表:
学生序号 1 2 3 4 5 6
身高差值(cm) +2 x +3 ﹣1 ﹣4 ﹣1
据此判断,2号学生的身高为 _____cm.
16.(本题3分)某同学参加校艺术节独唱比赛,其中唱功、表情、动作三个方面得分分别为90分、80分、95分,综合成绩中唱功占70%,表情占10%,动作占20%,则该名同学综合成绩为_______分.
17.(本题3分)为庆祝中国共产党建党100周年,某校开展主题为《党在我心中》的绘画、书法、摄影等艺术作品征集活动,从八年级5个班收集到的作品数量(单位:件)分别为50,40,30,70,60,则这组数据的平均数是_________.
18.(本题3分)已知7,4,5和x的平均数是6,则_________.
19.(本题3分)某校5个小组在一次植树活动中植树株数的统计图如图所示,则平均每组植树___________株.
20.(本题3分)如果一组数据中有3个6、4个,2个、1个0和3个x,其平均数为x,那么______.
三、解答题(共60分)
21.(本题12分)某公司欲招聘一名销售人员,按1:3的比例入围的甲、乙、丙(笔试成绩没有相同的,按从高到低排列,)三位入围者的成绩(百分制,成绩都是整数)如下表:
入围者 笔试成绩 面试成绩
甲 90 86
乙 x x
丙 84 92
(1)若公司认为笔试成绩与面试成绩同等重要,结果乙被录取,求x的值;
(2)若公司认为笔试成绩与面试成绩按4:6的权重,结果乙排第二,丙被录取,求x的值;
(3)若公司认为笔试成绩与面试成绩按a:(10-a)(a为1~9的整数)的权重,为确保甲被录取,求a的最小值.
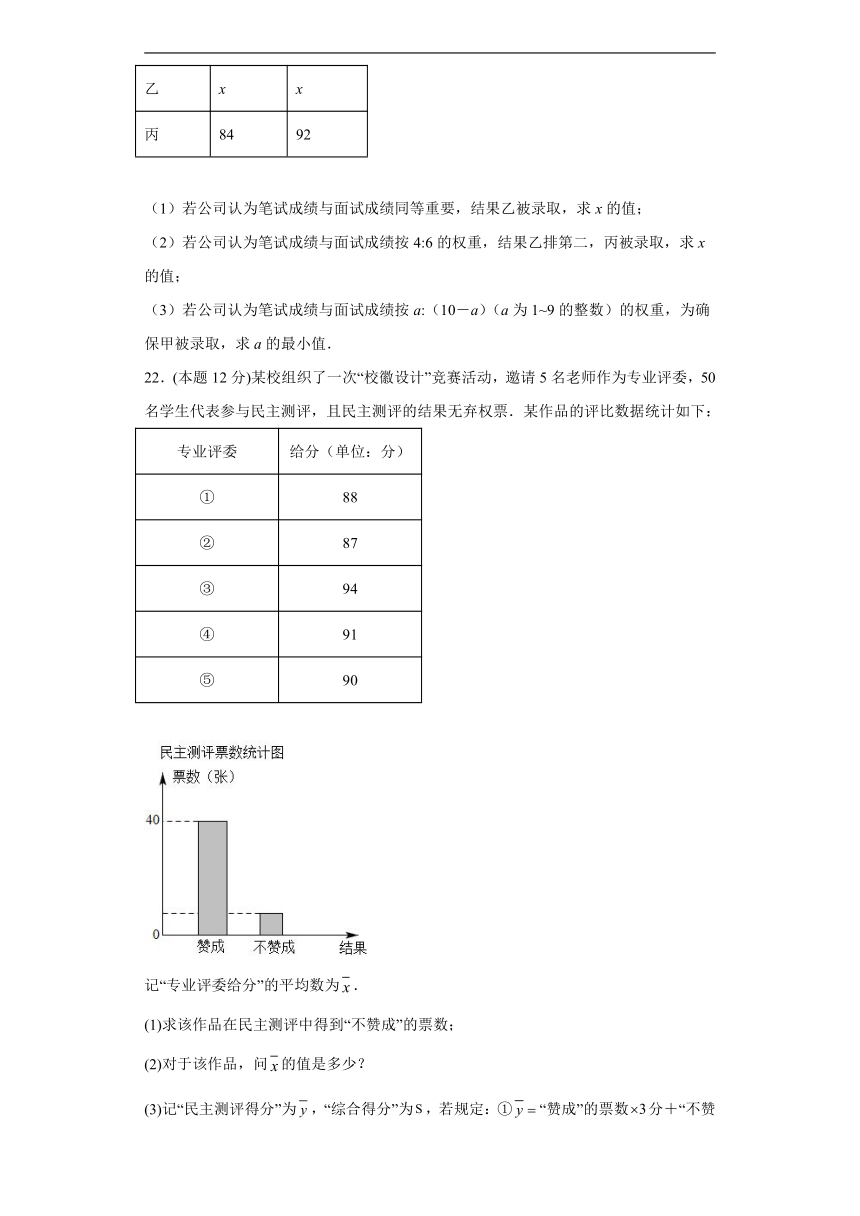
22.(本题12分)某校组织了一次“校徽设计”竞赛活动,邀请5名老师作为专业评委,50名学生代表参与民主测评,且民主测评的结果无弃权票.某作品的评比数据统计如下:
专业评委 给分(单位:分)
① 88
② 87
③ 94
④ 91
⑤ 90
记“专业评委给分”的平均数为.
(1)求该作品在民主测评中得到“不赞成”的票数;
(2)对于该作品,问的值是多少?
(3)记“民主测评得分”为,“综合得分”为,若规定:①“赞成”的票数分+“不赞成”的票数分;②.求该作品的“综合得分”的值.
23.(本题12分)请你根据给出的信息解答下列问题:某市疫情统计如下:共有200名患者,图1是该市轻症、重症、危重症三类患者的人数分布统计图不完整,图2是这三类患者的人均治疗费用统计图.请回答下列问题.
(1)轻症患者的人数是多少?
(2)该市为治疗危重症患者共花费多少万元?
(3)所有患者的平均治疗费用是多少万元?
24.(本题12分)某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试,各项满分均为10分,成绩高者被录用.图1是甲、乙测试成绩的条形统计图.
(1)分别求出甲、乙三项成绩之和,并指出会录用谁;
(2)若将甲、乙的三项测试成绩,按照扇形统计图(图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.
25.(本题12分)学校举办演讲比赛,总评成绩由“内容、表达、风度、印象”四部分组成.九(1)班组织选拔赛,制定的各部分所占比例如图,三位同学的成绩如表.请解答下列问题:
演讲总评成绩各部分所占比例的统计图:
三位同学的成绩统计表:
内容 表达 风度 印象 总评成绩
小明 8 7 8 8 m
小亮 7 8 8 9 7.85
小田 7 9 7 7 7.8
(1)求图中表示“内容”的扇形的圆心角度数.
(2)求表中m的值,并根据总评成绩确定三人的排名顺序.
(3)学校要求“内容”比“表达”重要,该统计图中各部分所占比例是否合理?如果不合理,如何调整?
参考答案:
1.A
2.C
3.D
4.A
5.B
6.A
7.C
8.B
9.D
10.B
11.李玉
12.12.5
13.
14.
15.##
16.90
17.50
18.8
19.5
20.1
21.(1)x=89;(2)x=88;(3)a的最小值为8
22.(1)10张
(2)90分
(3)96分
23.(1)160人
(2)100万元
(3)2.15万元
24.(1)甲
(2)乙
25.(1);
(2),三人成绩从高到低的排名顺序为:小亮,小田,小明;
(3)班级制定的各部分所占比例不合理,见解析;
一、单选题(共30分)
1.(本题3分)已知两组数据x,x2,…,xn和y1,y2,…,yn的平均数分别为2和-2,则x1+3y1,x2+3y2,…,xn+3yn的平均数为( )
A.-4 B.-2 C.0 D.2
2.(本题3分)已知一组数据1,0,3,-1,x,2,3的平均数是1,则这组数据的众数是( )
A.-1 B.3 C.-1和3 D.1和3
3.(本题3分)小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分 C.84.5分 D.86分
4.(本题3分)九龙坡区在中学生中开展了主题为“中华魂”的知识比赛,主要比赛项目为写作、阅读和演讲,量化评分标准比重分别为3∶2∶5,某学生写作,阅读和演讲三个项目得分分别为91分、80分、96分,则该生最后得分为( )
A.91.3 B.90 C.89 D.86.5
5.(本题3分)甲、乙、丙三种糖果售价分别为每千克6元,7元,8元,若将甲种8千克,乙种10千克,丙种3千克糖果混在一起,则售价应定为每千克( )
A.6.7元 B.6.8元 C.7.5元 D.8.6元
6.(本题3分)在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为y;同时去掉一个最高分和一个最低分,平均分为z,则( )
A.y>z>x B.x>z>y C.y>x>z D.z>y>x
7.(本题3分)2022年2月,第24届冬季奥林匹克运动会在北京举行.某校八年级(1)班在班会课开展了冬奥会知识小竞赛,10位同学在这个知识竞赛中的成绩统计结果如表所示,则这10位同学的平均成绩是( )
成绩 7 8 9 10
人数 1 4 3 2
A.8 B.8.5 C.8.6 D.9
8.(本题3分)一组数据4、5、6、a、b的平均数为5,则a、b的平均数为( )
A.4 B.5 C.8 D.10
9.(本题3分)有一组数据:2,5,5,6,7,每个数据加1后的平均数为( )
A.3 B.4 C.5 D.6
10.(本题3分)10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是( )
A. B. C. D.
二、填空题(共30分)
11.(本题3分)学校要从王静,李玉两同学中选拔一人参加运动会志愿者工作,选拔项目为普通话,体育知识和旅游知识.并将成绩依次按4∶3∶3计分. 两人的各项选拔成绩如下表所示,则最终胜出的同学是____.
普通话 体育知识 旅游知识
王静 80 90 70
李玉 90 80 70
12.(本题3分)已知数据,,, 的平均数为10,则数据,,,的平均数是______.
13.(本题3分)某水果店销售11元,18元,24元三种价格的水果,根据水果店一个月这三种水果销售量的统计图如图,可计算出该店当月销售出水果的平均价格是______元
14.(本题3分)在植树节当天,某班的四个绿化小组植树的棵数如下:10,8,9,9,则这组数据的平均数是___________.
15.(本题3分)某小组6名学生的平均身高为acm,规定超过acm的部分记为正数,不足acm的部分记为负数,他们的身高与平均身高的差值情况记录如下表:
学生序号 1 2 3 4 5 6
身高差值(cm) +2 x +3 ﹣1 ﹣4 ﹣1
据此判断,2号学生的身高为 _____cm.
16.(本题3分)某同学参加校艺术节独唱比赛,其中唱功、表情、动作三个方面得分分别为90分、80分、95分,综合成绩中唱功占70%,表情占10%,动作占20%,则该名同学综合成绩为_______分.
17.(本题3分)为庆祝中国共产党建党100周年,某校开展主题为《党在我心中》的绘画、书法、摄影等艺术作品征集活动,从八年级5个班收集到的作品数量(单位:件)分别为50,40,30,70,60,则这组数据的平均数是_________.
18.(本题3分)已知7,4,5和x的平均数是6,则_________.
19.(本题3分)某校5个小组在一次植树活动中植树株数的统计图如图所示,则平均每组植树___________株.
20.(本题3分)如果一组数据中有3个6、4个,2个、1个0和3个x,其平均数为x,那么______.
三、解答题(共60分)
21.(本题12分)某公司欲招聘一名销售人员,按1:3的比例入围的甲、乙、丙(笔试成绩没有相同的,按从高到低排列,)三位入围者的成绩(百分制,成绩都是整数)如下表:
入围者 笔试成绩 面试成绩
甲 90 86
乙 x x
丙 84 92
(1)若公司认为笔试成绩与面试成绩同等重要,结果乙被录取,求x的值;
(2)若公司认为笔试成绩与面试成绩按4:6的权重,结果乙排第二,丙被录取,求x的值;
(3)若公司认为笔试成绩与面试成绩按a:(10-a)(a为1~9的整数)的权重,为确保甲被录取,求a的最小值.
22.(本题12分)某校组织了一次“校徽设计”竞赛活动,邀请5名老师作为专业评委,50名学生代表参与民主测评,且民主测评的结果无弃权票.某作品的评比数据统计如下:
专业评委 给分(单位:分)
① 88
② 87
③ 94
④ 91
⑤ 90
记“专业评委给分”的平均数为.
(1)求该作品在民主测评中得到“不赞成”的票数;
(2)对于该作品,问的值是多少?
(3)记“民主测评得分”为,“综合得分”为,若规定:①“赞成”的票数分+“不赞成”的票数分;②.求该作品的“综合得分”的值.
23.(本题12分)请你根据给出的信息解答下列问题:某市疫情统计如下:共有200名患者,图1是该市轻症、重症、危重症三类患者的人数分布统计图不完整,图2是这三类患者的人均治疗费用统计图.请回答下列问题.
(1)轻症患者的人数是多少?
(2)该市为治疗危重症患者共花费多少万元?
(3)所有患者的平均治疗费用是多少万元?
24.(本题12分)某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试,各项满分均为10分,成绩高者被录用.图1是甲、乙测试成绩的条形统计图.
(1)分别求出甲、乙三项成绩之和,并指出会录用谁;
(2)若将甲、乙的三项测试成绩,按照扇形统计图(图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.
25.(本题12分)学校举办演讲比赛,总评成绩由“内容、表达、风度、印象”四部分组成.九(1)班组织选拔赛,制定的各部分所占比例如图,三位同学的成绩如表.请解答下列问题:
演讲总评成绩各部分所占比例的统计图:
三位同学的成绩统计表:
内容 表达 风度 印象 总评成绩
小明 8 7 8 8 m
小亮 7 8 8 9 7.85
小田 7 9 7 7 7.8
(1)求图中表示“内容”的扇形的圆心角度数.
(2)求表中m的值,并根据总评成绩确定三人的排名顺序.
(3)学校要求“内容”比“表达”重要,该统计图中各部分所占比例是否合理?如果不合理,如何调整?
参考答案:
1.A
2.C
3.D
4.A
5.B
6.A
7.C
8.B
9.D
10.B
11.李玉
12.12.5
13.
14.
15.##
16.90
17.50
18.8
19.5
20.1
21.(1)x=89;(2)x=88;(3)a的最小值为8
22.(1)10张
(2)90分
(3)96分
23.(1)160人
(2)100万元
(3)2.15万元
24.(1)甲
(2)乙
25.(1);
(2),三人成绩从高到低的排名顺序为:小亮,小田,小明;
(3)班级制定的各部分所占比例不合理,见解析;
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
