第三单元 函数中考复习测试题(含答案)
文档属性
| 名称 | 第三单元 函数中考复习测试题(含答案) |

|
|
| 格式 | docx | ||
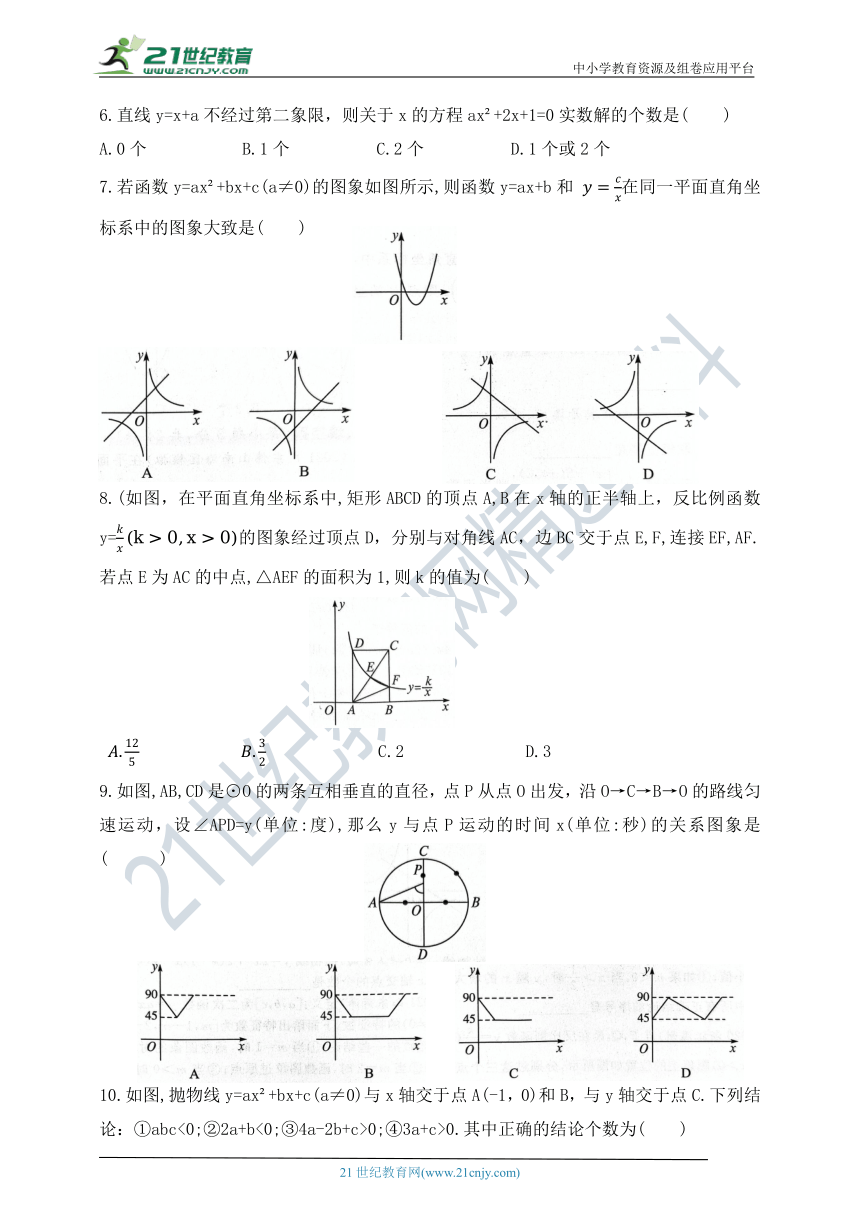
| 文件大小 | 11.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三单元函数检测题
一、选择题(每小题3分,共30分)
1.在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是( )
A.1 D.4或-4
2.如图,已知直线 :y=-2x+4与坐标轴分别交于A、B两点,那么过原点O且将△AOB的面积平分的直线 的解析式为( )
3.有一个装有水的容器,如图所示,容器内的水面高度是10cm.现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )
A.正比例函数关系 B.一次函数关系 C.二次函数关系 D.反比例函数关系
4.已知抛物线y=a(x-h) +k与x轴有两个交点A(-1,0),B(3,0),抛物线y=a(x-h-m) +k与x轴的一个交点是(4,0),则m的值是( )
A.5 B.-1 C.5或1 D.-5或-1
5.如图,正比例函数的图象与反比例函数 的图象相交于A,B两点,点B的横坐标为2,当y >y 时,x的取值范围是( )
A.x<-2或x>2 B.-22 C.x<-2或06.直线y=x+a不经过第二象限,则关于x的方程ax +2x+1=0实数解的个数是( )
A.0个 B.1个 C.2个 D.1个或2个
7.若函数y=ax +bx+c(a≠0)的图象如图所示,则函数y=ax+b和 在同一平面直角坐标系中的图象大致是( )
8.(如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,△AEF的面积为1,则k的值为( )
C.2 D.3
9.如图,AB,CD是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→B→O的路线匀速运动,设∠APD=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图象是( )
10.如图,抛物线y=ax +bx+c(a≠0)与x轴交于点A(-1,0)和B,与y轴交于点C.下列结论:①abc<0;②2a+b<0;③4a-2b+c>0;④3a+c>0.其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分)
11.在平面直角坐标系中,线段AB在x轴上,AB=2,且点 则点B的坐标是_______.
12.在函数 中,自变量x的取值范围是_____________.
13.若函数 则当函数值y=8时,自变量x的值等于___________.
14.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=-2x +4x+1,喷出水珠的最大高度是____________m.
15.如图,直线 与双曲线 相交于点A(m,2),则不等式 的解集是_____________.
16.抛物线y=2x +2(k-1)x-k(k为常数)与x轴交点的个数是______________.
17.定义:[a,b,c]为二次函数y=ax +bx+c(a≠0)的特征数,下面给出特征数为[m,1-m,2-m]的二次函数的一些结论:①当m=1时,函数图象的对称轴是y轴;②当m=2时,函数图象过原点;③当m>0时,函数有最小值;④如果m<0,当 时,y随x的增大而减小.其中所有正确结论的序号是_____________.
18.点P,Q,R在反比例函数 (常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S ,S ,S .若OE=ED=DC,S +S =27,则S 的值为_____________.
三、解答题(共66分)
19.(8分)甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离y (单位:m)与时间x(单位:min)之间的函数关系如图所示.
(1)在图中画出乙离A地的距离y (单位:m)与时间x之间的函数图象;
(2)若甲比乙晚5 min到达B地,求甲整个行程所用的时间.
20.(10分)小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
(1)求y与x之间的函数关系式;
(2)当x的值为6,8,10时,对应的函数值分别为y ,y ,y ,比较(y -y )与(y -y )的大小:y -y ________ y —y .
21.(10分)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,-4),B(2,0),交反比例函数 的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0(1)求一次函数和反比例函数的表达式;
(2)求△DPQ面积的最大值.
22.(12分)已知二次函数y =ax +bx+1,y =x +bx+a(a,b是实数,a≠0).
(1)若b≠0,且函数y 和函数y 的对称轴关于y轴对称,求a的值;
(2)若函数y 的图象过点(b,9a),求函数y 的图象与x轴的交点个数;
(3)设函数y ,y 的图象两个交点的纵坐标分别为m,n,求证:|m-n|的值与a无关.
23.(14分)如图,在平面直角坐标系中,抛物线y=ax +bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB.点P是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若PC∥AB,求点P的坐标;
(3)连接AC,求△PAC面积的最大值及此时点P的坐标.
24.(12分)某网店销售一款市场上畅销的蒸蛋器,进价为每个40元,在销售过程中发现,这款蒸蛋器销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.
(1)请直接写出y(个)与x(元)之间的函数关系式;
(2)当销售单价是多少元时,该网店每星期的销售利润是2400元
(3)当销售单价是多少元时,该网店每星期的销售利润最大 最大利润是多少元
参考答案
1.B
2.D 如图,当y=0,-2x+4=0,解得x=2,则A(2,0);当x=0,y=-2x+4=4,则B(0,4),∴AB的中点坐标为(1,2),∵直线l 把△AOB面积平分,∴l 经过AB的中点;
设直线l 的解析式为y=kx,把(1,2)代入得2=k,解得k=2,∴l 的解析式为y=2x.
3.B 设容器内的水面高度为h,注水时间为t,根据题意,得h=0.2t+10,∴容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是一次函数关系.
4.C ∵抛物线y=a(x-h) +k的对称轴为直线x=h,抛物线y=a(x-h-m) +k的对称轴为直线x=h+m,∴当点A(-1,0)向右平移5个单位后的对应点为(4,0),则m=4-(-1)=5;当点B(3,0)向右平移1个单位后的对应点为(4,0),则m=4-3=1,即m的值为5或1.
5.C 由反比例函数与正比例函数相交于点A,B,可得点A坐标与点B坐标关于原点对称.故点A的横坐标为-2.当y >y 时,即正比例函数图象在反比例图象上方,观察图象可得,当x<-2或06.D ∵直线y=x+a不经过第二象限,∴a≤0,当a=0时,方程为2x+1=0,解得x=当a≠0时,△=2 -4a>0,∴方程有两个不相等的实数根.故实数解的个数是1个或2个.
7.B 因为抛物线开口向上,说明a>0;又抛物线与y轴交点位于x轴上方知c>0;再根据对称轴 得到b<0;从而确定直线y=ax+b经过第一、三、四象限,双曲线 位于第一、三象限,故选B.
8.D 设A(a,0),∵四边形ABCD是矩形, 为AC的中点,∴E也为BD的中点,∵点B在x轴上,∴E的纵坐标为 E为AC的中点,∴点 ∴点 ∵△AEF的面积为1, 解得k=3.
9.B ①当点P沿O→C运动时,当点P在点O的位置时,y=90°,当点P在点C的位置时,∵OA=OC,∴y=45°,∴y由90°逐渐减小到45°;
②当点P沿C→B运动时,根据圆周角定理,得y≡90°÷2=45°;
③当点P沿B→O运动时,当点P在点B的位置时,y=45°,当点P在点O的位置时,y=90°,∴y由45°逐渐增加到90°.
10.B ①∵抛物线的开口向上,∴a>0.∵对称轴位于y轴的右侧,∴b<0.∵抛物线与y轴交于负半轴,∴c<0,∴abc>0,故①错误;
②对称轴为 得2a>-b,即2a+b>0,故②错误;
③如图,当x=-2时,y>0,4a-2b+c>0,故③正确;
④∵当x=-1时,y=0,∴0=a-b+c0,故④正确.
或 ∵线段AB在x轴上,AB=2,且点 ①点B在点A的右边,B点的横坐标为:
②点B在点A的左边,B点的横坐标为:∴点B的坐标为: 0)或
13.4或
14.3 ∵y=-2x +4x+1=-2(x-1) +3,∴当x=1时,y有最大值为3,∴喷出水珠的最大高度是3m.
15.-42
∵点A(m,2)在直线 上, 解得m=2.则A(2,2),
将其代入双曲线 得到k=2×2=4,∴双曲线的解析式为
解得 或
∴直线 与双曲线 的另一交点坐标是(-4,-1).
∴不等式 的解集是-42.
17.①②③ 由特征数的定义可得:特征数为[m,1-m,2-m]的二次函数的表达式为y=mx +(1-m)x+2-m.∵此抛物线的对称轴为直线 ∴当m=1时,对称轴为直线x=0,即y轴,故①正确;∵当m=2时,此二次函数表达式为y=2x -x,令x=0,则y=0,∴函数图象过原点,故②正确;∵当m>0时,二次函数图象开口向上,函数有最小值,故③正确;∵m<0,∴对称轴 抛物线开口向下,∴在对称轴的右侧,y随x的增大而减小.即 时,y随x的增大而减小,故④错误.
∴可以假设CD=DE=OE=a,则
∵S +S =27,
19.解(1)如图:
(2)设甲的速度是vm/min,乙整个行程所用的时间为t min,
由题意得2v·t=(t+1+5)v,解得t=6.6+1+5=12(min).
答:甲整个行程所用的时间为12 min.
20.解(1)设y与x之间的函数关系式为 把(3,400)代入 得 解得
k=1200.故y与x之间的函数关系式为
(2)>
把x=6,8,10分别代入 得y = 120,-y =200-150=50,y -y =150-120=30,50>30,∴y -y >y -y .
解(1)把A(0,-4),B(2,0)代入一次函数y=kx+b,
得解得 故一次函数的表达式为y=2x-4.
∵当x=3时,y=2×3-4=2,∴点C(3,2).
∵点C在反比例函数的图象上,∴k=3×2=6,
∴反比例函数的表达式为
(2)∵点P在反比例函数的图象上,点Q在一次函数的图象上,
∴点 点Q(n,2n-4),
=-n +2n+3=-(n-1) +4.
∴当n=1时,即△DPQ面积的最大值是4.
22.解(1)根据题意知:
∵b≠0,∴a=-1;
(2)将点(b,9a)代入y =x +bx+a,得b +b·b+a=9a.整理得b -4a=0.
令y =0,则ax +bx+1=0,∴△=b -4a×1=0.
∴函数y 的图象与x轴只有一个交点;
(3)证明:设函数y ,y 的图象两个交点的横坐标分别是p,t,
则m=p +bp+a,n=t +bt+a.
∴|m-n|=|(p +bp+a)-(t +bt+a)|=|(p -t )+b(p-t)| ,∴|m-n|的值与a无关.
23.解(1)抛物线y=ax +bx-2,则c=-2,故OC=2,
而OA=2OC=8OB,则
故点A,B,C的坐标分别为 ,(0,-2).
则 故a=1,
故抛物线的表达式为
(2)抛物线的对称轴为
当PC∥AB时,点P,C的纵坐标相同,根据函数的对称性得点
(3)如图,过点P作PH∥y轴交AC于点H.
由点A,C的坐标,得直线AC的表达式为y
则△PAC的面积
∵-2<0,∴S有最大值,当x=-2时,S的最大值为8,此时点P的坐标为(-2,-5).
24.解(1)由题意,得:y=100-2(x-60)=-2x+220,∴y=-2x+220;
(2)设利润为W,则W=(x-40)y=(x-40)(-2x+220)=-2x +300x-8800,
令W=2400,则-2x +300x-8800=2400,解得:x=70或x=80,
答:当销售单价为70元或80元时,每星期的销售利润恰为2400元;
(3)W=-2x +300x-8800=-2(x-75) +2450,
∵-2<0,∴当x=75时,W有最大值,最大值为2450元,
答:销售单价为75元时利润最大,最大利润为2450元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三单元函数检测题
一、选择题(每小题3分,共30分)
1.在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是( )
A.1 D.4或-4
2.如图,已知直线 :y=-2x+4与坐标轴分别交于A、B两点,那么过原点O且将△AOB的面积平分的直线 的解析式为( )
3.有一个装有水的容器,如图所示,容器内的水面高度是10cm.现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )
A.正比例函数关系 B.一次函数关系 C.二次函数关系 D.反比例函数关系
4.已知抛物线y=a(x-h) +k与x轴有两个交点A(-1,0),B(3,0),抛物线y=a(x-h-m) +k与x轴的一个交点是(4,0),则m的值是( )
A.5 B.-1 C.5或1 D.-5或-1
5.如图,正比例函数的图象与反比例函数 的图象相交于A,B两点,点B的横坐标为2,当y >y 时,x的取值范围是( )
A.x<-2或x>2 B.-2
A.0个 B.1个 C.2个 D.1个或2个
7.若函数y=ax +bx+c(a≠0)的图象如图所示,则函数y=ax+b和 在同一平面直角坐标系中的图象大致是( )
8.(如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,△AEF的面积为1,则k的值为( )
C.2 D.3
9.如图,AB,CD是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→B→O的路线匀速运动,设∠APD=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图象是( )
10.如图,抛物线y=ax +bx+c(a≠0)与x轴交于点A(-1,0)和B,与y轴交于点C.下列结论:①abc<0;②2a+b<0;③4a-2b+c>0;④3a+c>0.其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分)
11.在平面直角坐标系中,线段AB在x轴上,AB=2,且点 则点B的坐标是_______.
12.在函数 中,自变量x的取值范围是_____________.
13.若函数 则当函数值y=8时,自变量x的值等于___________.
14.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=-2x +4x+1,喷出水珠的最大高度是____________m.
15.如图,直线 与双曲线 相交于点A(m,2),则不等式 的解集是_____________.
16.抛物线y=2x +2(k-1)x-k(k为常数)与x轴交点的个数是______________.
17.定义:[a,b,c]为二次函数y=ax +bx+c(a≠0)的特征数,下面给出特征数为[m,1-m,2-m]的二次函数的一些结论:①当m=1时,函数图象的对称轴是y轴;②当m=2时,函数图象过原点;③当m>0时,函数有最小值;④如果m<0,当 时,y随x的增大而减小.其中所有正确结论的序号是_____________.
18.点P,Q,R在反比例函数 (常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S ,S ,S .若OE=ED=DC,S +S =27,则S 的值为_____________.
三、解答题(共66分)
19.(8分)甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离y (单位:m)与时间x(单位:min)之间的函数关系如图所示.
(1)在图中画出乙离A地的距离y (单位:m)与时间x之间的函数图象;
(2)若甲比乙晚5 min到达B地,求甲整个行程所用的时间.
20.(10分)小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
(1)求y与x之间的函数关系式;
(2)当x的值为6,8,10时,对应的函数值分别为y ,y ,y ,比较(y -y )与(y -y )的大小:y -y ________ y —y .
21.(10分)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,-4),B(2,0),交反比例函数 的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0
(2)求△DPQ面积的最大值.
22.(12分)已知二次函数y =ax +bx+1,y =x +bx+a(a,b是实数,a≠0).
(1)若b≠0,且函数y 和函数y 的对称轴关于y轴对称,求a的值;
(2)若函数y 的图象过点(b,9a),求函数y 的图象与x轴的交点个数;
(3)设函数y ,y 的图象两个交点的纵坐标分别为m,n,求证:|m-n|的值与a无关.
23.(14分)如图,在平面直角坐标系中,抛物线y=ax +bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB.点P是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若PC∥AB,求点P的坐标;
(3)连接AC,求△PAC面积的最大值及此时点P的坐标.
24.(12分)某网店销售一款市场上畅销的蒸蛋器,进价为每个40元,在销售过程中发现,这款蒸蛋器销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.
(1)请直接写出y(个)与x(元)之间的函数关系式;
(2)当销售单价是多少元时,该网店每星期的销售利润是2400元
(3)当销售单价是多少元时,该网店每星期的销售利润最大 最大利润是多少元
参考答案
1.B
2.D 如图,当y=0,-2x+4=0,解得x=2,则A(2,0);当x=0,y=-2x+4=4,则B(0,4),∴AB的中点坐标为(1,2),∵直线l 把△AOB面积平分,∴l 经过AB的中点;
设直线l 的解析式为y=kx,把(1,2)代入得2=k,解得k=2,∴l 的解析式为y=2x.
3.B 设容器内的水面高度为h,注水时间为t,根据题意,得h=0.2t+10,∴容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是一次函数关系.
4.C ∵抛物线y=a(x-h) +k的对称轴为直线x=h,抛物线y=a(x-h-m) +k的对称轴为直线x=h+m,∴当点A(-1,0)向右平移5个单位后的对应点为(4,0),则m=4-(-1)=5;当点B(3,0)向右平移1个单位后的对应点为(4,0),则m=4-3=1,即m的值为5或1.
5.C 由反比例函数与正比例函数相交于点A,B,可得点A坐标与点B坐标关于原点对称.故点A的横坐标为-2.当y >y 时,即正比例函数图象在反比例图象上方,观察图象可得,当x<-2或0
7.B 因为抛物线开口向上,说明a>0;又抛物线与y轴交点位于x轴上方知c>0;再根据对称轴 得到b<0;从而确定直线y=ax+b经过第一、三、四象限,双曲线 位于第一、三象限,故选B.
8.D 设A(a,0),∵四边形ABCD是矩形, 为AC的中点,∴E也为BD的中点,∵点B在x轴上,∴E的纵坐标为 E为AC的中点,∴点 ∴点 ∵△AEF的面积为1, 解得k=3.
9.B ①当点P沿O→C运动时,当点P在点O的位置时,y=90°,当点P在点C的位置时,∵OA=OC,∴y=45°,∴y由90°逐渐减小到45°;
②当点P沿C→B运动时,根据圆周角定理,得y≡90°÷2=45°;
③当点P沿B→O运动时,当点P在点B的位置时,y=45°,当点P在点O的位置时,y=90°,∴y由45°逐渐增加到90°.
10.B ①∵抛物线的开口向上,∴a>0.∵对称轴位于y轴的右侧,∴b<0.∵抛物线与y轴交于负半轴,∴c<0,∴abc>0,故①错误;
②对称轴为 得2a>-b,即2a+b>0,故②错误;
③如图,当x=-2时,y>0,4a-2b+c>0,故③正确;
④∵当x=-1时,y=0,∴0=a-b+c
或 ∵线段AB在x轴上,AB=2,且点 ①点B在点A的右边,B点的横坐标为:
②点B在点A的左边,B点的横坐标为:∴点B的坐标为: 0)或
13.4或
14.3 ∵y=-2x +4x+1=-2(x-1) +3,∴当x=1时,y有最大值为3,∴喷出水珠的最大高度是3m.
15.-4
∵点A(m,2)在直线 上, 解得m=2.则A(2,2),
将其代入双曲线 得到k=2×2=4,∴双曲线的解析式为
解得 或
∴直线 与双曲线 的另一交点坐标是(-4,-1).
∴不等式 的解集是-4
17.①②③ 由特征数的定义可得:特征数为[m,1-m,2-m]的二次函数的表达式为y=mx +(1-m)x+2-m.∵此抛物线的对称轴为直线 ∴当m=1时,对称轴为直线x=0,即y轴,故①正确;∵当m=2时,此二次函数表达式为y=2x -x,令x=0,则y=0,∴函数图象过原点,故②正确;∵当m>0时,二次函数图象开口向上,函数有最小值,故③正确;∵m<0,∴对称轴 抛物线开口向下,∴在对称轴的右侧,y随x的增大而减小.即 时,y随x的增大而减小,故④错误.
∴可以假设CD=DE=OE=a,则
∵S +S =27,
19.解(1)如图:
(2)设甲的速度是vm/min,乙整个行程所用的时间为t min,
由题意得2v·t=(t+1+5)v,解得t=6.6+1+5=12(min).
答:甲整个行程所用的时间为12 min.
20.解(1)设y与x之间的函数关系式为 把(3,400)代入 得 解得
k=1200.故y与x之间的函数关系式为
(2)>
把x=6,8,10分别代入 得y = 120,-y =200-150=50,y -y =150-120=30,50>30,∴y -y >y -y .
解(1)把A(0,-4),B(2,0)代入一次函数y=kx+b,
得解得 故一次函数的表达式为y=2x-4.
∵当x=3时,y=2×3-4=2,∴点C(3,2).
∵点C在反比例函数的图象上,∴k=3×2=6,
∴反比例函数的表达式为
(2)∵点P在反比例函数的图象上,点Q在一次函数的图象上,
∴点 点Q(n,2n-4),
=-n +2n+3=-(n-1) +4.
∴当n=1时,即△DPQ面积的最大值是4.
22.解(1)根据题意知:
∵b≠0,∴a=-1;
(2)将点(b,9a)代入y =x +bx+a,得b +b·b+a=9a.整理得b -4a=0.
令y =0,则ax +bx+1=0,∴△=b -4a×1=0.
∴函数y 的图象与x轴只有一个交点;
(3)证明:设函数y ,y 的图象两个交点的横坐标分别是p,t,
则m=p +bp+a,n=t +bt+a.
∴|m-n|=|(p +bp+a)-(t +bt+a)|=|(p -t )+b(p-t)| ,∴|m-n|的值与a无关.
23.解(1)抛物线y=ax +bx-2,则c=-2,故OC=2,
而OA=2OC=8OB,则
故点A,B,C的坐标分别为 ,(0,-2).
则 故a=1,
故抛物线的表达式为
(2)抛物线的对称轴为
当PC∥AB时,点P,C的纵坐标相同,根据函数的对称性得点
(3)如图,过点P作PH∥y轴交AC于点H.
由点A,C的坐标,得直线AC的表达式为y
则△PAC的面积
∵-2<0,∴S有最大值,当x=-2时,S的最大值为8,此时点P的坐标为(-2,-5).
24.解(1)由题意,得:y=100-2(x-60)=-2x+220,∴y=-2x+220;
(2)设利润为W,则W=(x-40)y=(x-40)(-2x+220)=-2x +300x-8800,
令W=2400,则-2x +300x-8800=2400,解得:x=70或x=80,
答:当销售单价为70元或80元时,每星期的销售利润恰为2400元;
(3)W=-2x +300x-8800=-2(x-75) +2450,
∵-2<0,∴当x=75时,W有最大值,最大值为2450元,
答:销售单价为75元时利润最大,最大利润为2450元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
