人教版(2019)选择性必修第一册2.2 简谐运动的描述(共22张ppt)
文档属性
| 名称 | 人教版(2019)选择性必修第一册2.2 简谐运动的描述(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-10-05 16:24:21 | ||
图片预览








文档简介
(共22张PPT)
一、描述简谐运动的物理量
1、振幅A
(1)定义:振动物体离开平衡位置的最大距离。是标量。
(2)物理意义:描述振动强弱的物理量。
A
简谐运动中
OA = OB
振幅的两倍(2A)表示振动物体运动范围
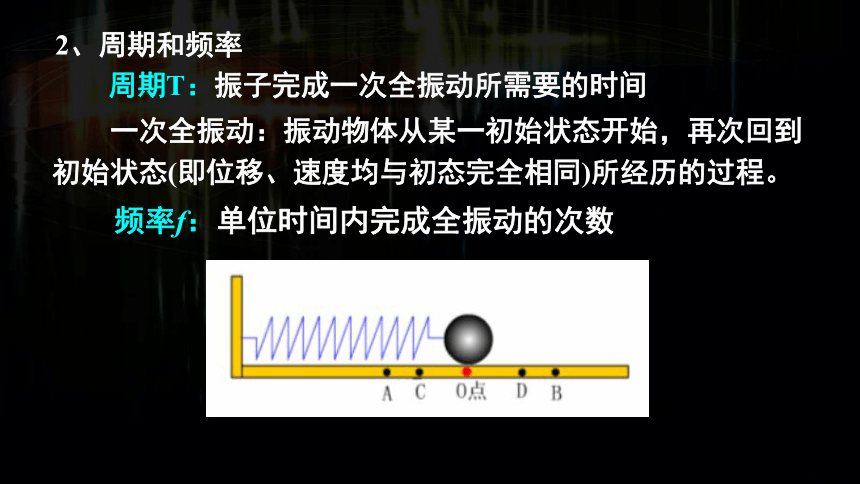
2、周期和频率
周期T:振子完成一次全振动所需要的时间
一次全振动:振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
频率f:单位时间内完成全振动的次数
问题1:O—D—B—D—O是一个周期吗?
问题2:若从振子经过C向右起,经过怎样的运动才叫完成一次全振动?
附:简谐运动的周期公式
简谐运动的周期和频率由振动系统本身的因素决定,与振幅无关
3、相位:
描述周期性运动的物体在各个时刻所处状态的物理量。
二、简谐运动的表达式
以x代表质点对于平衡位置的位移,t代表时间,则
1、公式中的A 代表什么
2、ω叫做什么 它和T、f之间有什么关系
3、公式中的相位用什么来表示
4、什么叫简谐振动的初相
振幅
初相位
相位
周期
频率
实际上经常用到的是两个相同频率的简谐运动的相位差,简称相差
同相:频率相同、初相相同(即相差为0)的两个振子振动步调完全相同
反相:频率相同、相差为π的两个振子振动步调完全相反
两个简谐振动分别为
x1=4asin(4πbt+ π)
x2=2asin(4πbt+ π)
求它们的振幅之比,各自的频率,以及它的相位差.
练习
小 结
一、描述简谐运动的物理量
1、振幅A:振动物体离开平衡位置的最大距离
2、周期T:完成一次全振动所需要的时间
频率f:单位时间内完成全振动的次数关系T=1/f
3、相位:周期性运动的物体在各个时刻所处的不同的状
态
二、简谐运动的表达式
1.右图中是甲乙两弹簧振子的振动图象,两振动振幅之比为________,频率之比为______,甲和乙的
相差为_______
2.某简谐运动的位移与时间关系为:
x=0.1sin(100πt+π)cm, 由此可知该振动的振幅
是______cm,频率是____Hz,零时刻振动物体的速
度与规定正方向_____(填“相同”或“相反”).
课 堂 训 练
2∶1
1∶1
0.1
50
相反
3、有一个在光滑水平面内的弹簧振子,第一次用力把弹簧压缩x后释放,第二次把弹簧压缩2x后释放,则先后两次振动的周期和振幅之比分别为多少?
1:1
1:2
4、弹簧振子以O点为平衡位置,在B、C两点之间做简谐振动,B、C相距20cm,某时刻振子处于B点,经过0.5s,振子首次到达C点,求:
(1)振子的周期和频率
(2)振子在5s末的位移的大小
(3)振子5s内通过的路程
T=1.0s f=1 Hz
10cm
200cm
注意:
T内通过的路程一定是4A
1/2T内通过的路程一定是2A
1/4T内通过的路程不一定是A
1、相位每增加2π就意味着发生了一次全振动
2、意味着乙总是比甲滞后1/4个周期或1/4次全振动.
1、一个物体运动时其相位变化多少就意味着完成了一次全振动
2、甲和乙两个简谐运动的相差为 ,意味着什么
【例题】
如图2.2-5,弹簧振子的平衡位置为О点,在B、C两点之间做简谐运动。B、C相距20 cm。小球经过B点时开始计时,经过0.5s首次到达C点。
(1)画出小球在第一个周期内的x-t图像。
(2)求5s内小球通过的路程及5s末小球的
位移。
1. 一个小球在平街位置О点附近做简谐运动, 若从O点开始计时, 经过3s小球第一次经过M点,再继续运动,又经过2s它第二次经过M点: 求该小球做简谐运动的可能周期。
2. 有两个简谐运动: x1= 3asin ( 8πbt + )和x2=9asin( 8πbt+ ), 它们的振幅之比是多少 它们的频率各是多少 t=0时它们的相位差是多少
3. 图2.2-8是两个简谐运动的振动图像, 它们的相位差是多少
4. 有甲、乙两个简谐运动: 甲的振幅为2 cm,乙的振幅为3 cm, 它们的周期都是4 s,当t =0时甲的位移为2 cm, 乙的相位比甲落后 。请在问一坐标系中画出这两个简谐运动的位移—时间图像。
5. 图2.2-9为甲、乙两个简谐运动的振动图像。请根啬图像写出这两个简谐运动的位移随时间变化的关系式。
一、描述简谐运动的物理量
1、振幅A
(1)定义:振动物体离开平衡位置的最大距离。是标量。
(2)物理意义:描述振动强弱的物理量。
A
简谐运动中
OA = OB
振幅的两倍(2A)表示振动物体运动范围
2、周期和频率
周期T:振子完成一次全振动所需要的时间
一次全振动:振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
频率f:单位时间内完成全振动的次数
问题1:O—D—B—D—O是一个周期吗?
问题2:若从振子经过C向右起,经过怎样的运动才叫完成一次全振动?
附:简谐运动的周期公式
简谐运动的周期和频率由振动系统本身的因素决定,与振幅无关
3、相位:
描述周期性运动的物体在各个时刻所处状态的物理量。
二、简谐运动的表达式
以x代表质点对于平衡位置的位移,t代表时间,则
1、公式中的A 代表什么
2、ω叫做什么 它和T、f之间有什么关系
3、公式中的相位用什么来表示
4、什么叫简谐振动的初相
振幅
初相位
相位
周期
频率
实际上经常用到的是两个相同频率的简谐运动的相位差,简称相差
同相:频率相同、初相相同(即相差为0)的两个振子振动步调完全相同
反相:频率相同、相差为π的两个振子振动步调完全相反
两个简谐振动分别为
x1=4asin(4πbt+ π)
x2=2asin(4πbt+ π)
求它们的振幅之比,各自的频率,以及它的相位差.
练习
小 结
一、描述简谐运动的物理量
1、振幅A:振动物体离开平衡位置的最大距离
2、周期T:完成一次全振动所需要的时间
频率f:单位时间内完成全振动的次数关系T=1/f
3、相位:周期性运动的物体在各个时刻所处的不同的状
态
二、简谐运动的表达式
1.右图中是甲乙两弹簧振子的振动图象,两振动振幅之比为________,频率之比为______,甲和乙的
相差为_______
2.某简谐运动的位移与时间关系为:
x=0.1sin(100πt+π)cm, 由此可知该振动的振幅
是______cm,频率是____Hz,零时刻振动物体的速
度与规定正方向_____(填“相同”或“相反”).
课 堂 训 练
2∶1
1∶1
0.1
50
相反
3、有一个在光滑水平面内的弹簧振子,第一次用力把弹簧压缩x后释放,第二次把弹簧压缩2x后释放,则先后两次振动的周期和振幅之比分别为多少?
1:1
1:2
4、弹簧振子以O点为平衡位置,在B、C两点之间做简谐振动,B、C相距20cm,某时刻振子处于B点,经过0.5s,振子首次到达C点,求:
(1)振子的周期和频率
(2)振子在5s末的位移的大小
(3)振子5s内通过的路程
T=1.0s f=1 Hz
10cm
200cm
注意:
T内通过的路程一定是4A
1/2T内通过的路程一定是2A
1/4T内通过的路程不一定是A
1、相位每增加2π就意味着发生了一次全振动
2、意味着乙总是比甲滞后1/4个周期或1/4次全振动.
1、一个物体运动时其相位变化多少就意味着完成了一次全振动
2、甲和乙两个简谐运动的相差为 ,意味着什么
【例题】
如图2.2-5,弹簧振子的平衡位置为О点,在B、C两点之间做简谐运动。B、C相距20 cm。小球经过B点时开始计时,经过0.5s首次到达C点。
(1)画出小球在第一个周期内的x-t图像。
(2)求5s内小球通过的路程及5s末小球的
位移。
1. 一个小球在平街位置О点附近做简谐运动, 若从O点开始计时, 经过3s小球第一次经过M点,再继续运动,又经过2s它第二次经过M点: 求该小球做简谐运动的可能周期。
2. 有两个简谐运动: x1= 3asin ( 8πbt + )和x2=9asin( 8πbt+ ), 它们的振幅之比是多少 它们的频率各是多少 t=0时它们的相位差是多少
3. 图2.2-8是两个简谐运动的振动图像, 它们的相位差是多少
4. 有甲、乙两个简谐运动: 甲的振幅为2 cm,乙的振幅为3 cm, 它们的周期都是4 s,当t =0时甲的位移为2 cm, 乙的相位比甲落后 。请在问一坐标系中画出这两个简谐运动的位移—时间图像。
5. 图2.2-9为甲、乙两个简谐运动的振动图像。请根啬图像写出这两个简谐运动的位移随时间变化的关系式。
