高中数学人教A版必修第一册课课件2.2基本不等式 (课件共15张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课课件2.2基本不等式 (课件共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 223.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
2.2 基本不等式(一)
人教A版(2019)必修第一册
(1)理解重要不等式
基本不等式
(2)能够利用基本不等式求简单的最值。
的几何意义及代数意义;
二、自学指导
阅读课本P44--P46思考下列问题
1、课本是如何推出基本不等式的?
2、基本不等式表明了什么?
3、如何证明基本不等式?
4、使用基本不等式的条件有哪些?
一、学习目标
文字叙述:
三、新授
若a,b∈R,那么a2+b2≥2ab(当且仅当a=b时,等式成立)
重要不等式:
两数的平方和不小于积的2倍。
问题一
替换后得到:
即
化简:
你能用几何方法解释这个不等式吗?
问题二
我们把 叫做正数a,b的算术平均数, 叫做正数a,b的几何平均数。
文字叙述:两个正数的算术平均数不小于它们的几何平均数,因此也叫均值不等式;
从形的角度来看,基本不等式具有特定的几何意义;从数的角度来看,基本不等式揭示了“和”与“积”这两种结构间的不等关系;
正用、逆用,注意成立的条件
⑴ a、 b是两个正数;
⑵ 当且仅当a=b时,等号成立。
(当且仅当a=b时,等号成立。)
基本不等式
上面通过考察 的特殊情形获得了基本不等式。能否直接利用不等式的性质推导出基本不等式呢?下面我们一起来分析一下。
要证 ①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
要证④,只要证 ⑤
显然,⑤ 成立,当且仅当 时,⑤中的等号成立。
只要把上述过程倒过来,就能直接推出基本不等式了。
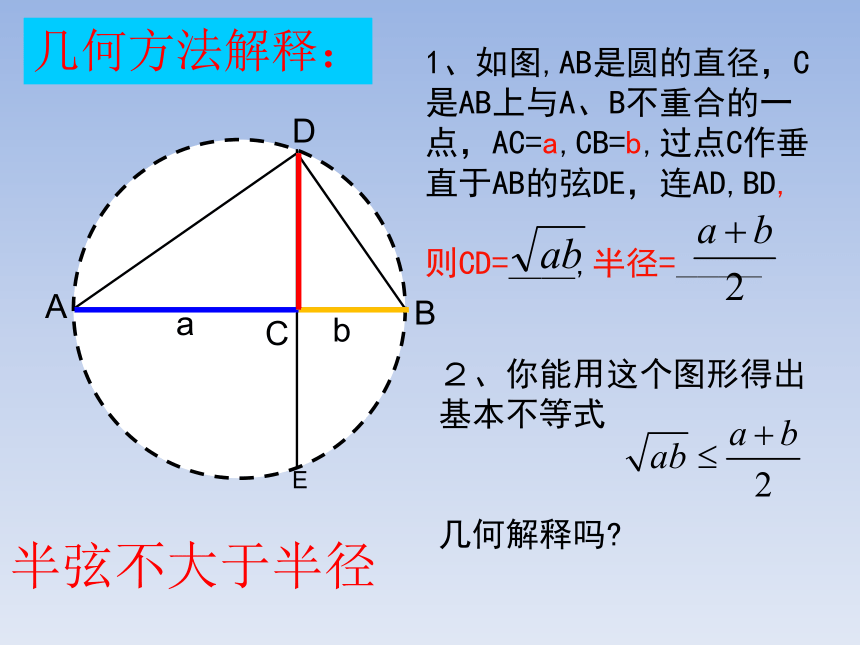
几何方法解释:
A
B
C
D
E
1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____
2、你能用这个图形得出基本不等式
几何解释吗
a
b
半弦不大于半径
例1.试判断 与 2 的大小关系?
变式:
试判断 与 2 的大小关系?
如果将条件“x>0” 去掉,上述结论是否仍然成立?
利用基本不等式解决最大(小)值问题
例2、已知 都是正数,求证
(1)如果积 是定值P,那么当 时,和 有最小值 ;
(2)如果和 是定值S,那么当 时,积 有最大值
(1)一正:各项均为正数
(2)二定:两个正数积为定值,和有最小值。
两个正数和为定值,积有最大值。
(3)三相等:求最值时一定要考虑不等式是否能取“=”,否则会出现错误
小结:利用 求最值时要注意下面三条:
“一正二定三等”,这三个条件缺一不可.
四、检测 :
下面几道题的解答可能有错,如果错了,那么错在哪里?
(1)已知函数 ,求函数的最小值和此时x的取值.
运用均值不等式的过程中,忽略了“正数”这个条件.
用均值不等式求最值,须满足“定值”这个条件.
(2)
用均值不等式求最值,必须注意 “相等” 的条件.
如果取等的条件不成立,则不能取到该最值.
(3)
所以函数的最小值为4
五、课堂小结
求最值时注意把握 “一正,二定,三相等”
已知 x, y 都是正数, P, S 是常数.
(1) xy=P x+y≥2 P(当且仅当 x=y 时, 取“=”号).
(2) x+y=S xy≤ S2(当且仅当 x=y 时, 取“=”号).
1
4
2. 利用基本不等式求最值
1. 两个重要的不等式
六、当堂训练
B
练1、下列函数的最小值为2的是
练2、求以下问题中的最值
(1)若a>0,则当a= 时, 有最小值
(2)正数x,y满足x+y=20,xy的最大值
12
100
1. 求函数 f(x)=x + (x> -1) 的最小值.
1
x+1
2. 若 0七、能力提升
2.2 基本不等式(一)
人教A版(2019)必修第一册
(1)理解重要不等式
基本不等式
(2)能够利用基本不等式求简单的最值。
的几何意义及代数意义;
二、自学指导
阅读课本P44--P46思考下列问题
1、课本是如何推出基本不等式的?
2、基本不等式表明了什么?
3、如何证明基本不等式?
4、使用基本不等式的条件有哪些?
一、学习目标
文字叙述:
三、新授
若a,b∈R,那么a2+b2≥2ab(当且仅当a=b时,等式成立)
重要不等式:
两数的平方和不小于积的2倍。
问题一
替换后得到:
即
化简:
你能用几何方法解释这个不等式吗?
问题二
我们把 叫做正数a,b的算术平均数, 叫做正数a,b的几何平均数。
文字叙述:两个正数的算术平均数不小于它们的几何平均数,因此也叫均值不等式;
从形的角度来看,基本不等式具有特定的几何意义;从数的角度来看,基本不等式揭示了“和”与“积”这两种结构间的不等关系;
正用、逆用,注意成立的条件
⑴ a、 b是两个正数;
⑵ 当且仅当a=b时,等号成立。
(当且仅当a=b时,等号成立。)
基本不等式
上面通过考察 的特殊情形获得了基本不等式。能否直接利用不等式的性质推导出基本不等式呢?下面我们一起来分析一下。
要证 ①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
要证④,只要证 ⑤
显然,⑤ 成立,当且仅当 时,⑤中的等号成立。
只要把上述过程倒过来,就能直接推出基本不等式了。
几何方法解释:
A
B
C
D
E
1、如图,AB是圆的直径,C是AB上与A、B不重合的一点,AC=a,CB=b,过点C作垂直于AB的弦DE,连AD,BD,
则CD=__,半径=____
2、你能用这个图形得出基本不等式
几何解释吗
a
b
半弦不大于半径
例1.试判断 与 2 的大小关系?
变式:
试判断 与 2 的大小关系?
如果将条件“x>0” 去掉,上述结论是否仍然成立?
利用基本不等式解决最大(小)值问题
例2、已知 都是正数,求证
(1)如果积 是定值P,那么当 时,和 有最小值 ;
(2)如果和 是定值S,那么当 时,积 有最大值
(1)一正:各项均为正数
(2)二定:两个正数积为定值,和有最小值。
两个正数和为定值,积有最大值。
(3)三相等:求最值时一定要考虑不等式是否能取“=”,否则会出现错误
小结:利用 求最值时要注意下面三条:
“一正二定三等”,这三个条件缺一不可.
四、检测 :
下面几道题的解答可能有错,如果错了,那么错在哪里?
(1)已知函数 ,求函数的最小值和此时x的取值.
运用均值不等式的过程中,忽略了“正数”这个条件.
用均值不等式求最值,须满足“定值”这个条件.
(2)
用均值不等式求最值,必须注意 “相等” 的条件.
如果取等的条件不成立,则不能取到该最值.
(3)
所以函数的最小值为4
五、课堂小结
求最值时注意把握 “一正,二定,三相等”
已知 x, y 都是正数, P, S 是常数.
(1) xy=P x+y≥2 P(当且仅当 x=y 时, 取“=”号).
(2) x+y=S xy≤ S2(当且仅当 x=y 时, 取“=”号).
1
4
2. 利用基本不等式求最值
1. 两个重要的不等式
六、当堂训练
B
练1、下列函数的最小值为2的是
练2、求以下问题中的最值
(1)若a>0,则当a= 时, 有最小值
(2)正数x,y满足x+y=20,xy的最大值
12
100
1. 求函数 f(x)=x + (x> -1) 的最小值.
1
x+1
2. 若 0
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
