高中数学人教A版必修第一册课课件2.2基本不等式 (课件共15张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课课件2.2基本不等式 (课件共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 19:35:04 | ||
图片预览





文档简介
(共15张PPT)
基本不等式(1)
重要不等式: ,a2+b2≥2ab,当且仅当 时,等号成立.
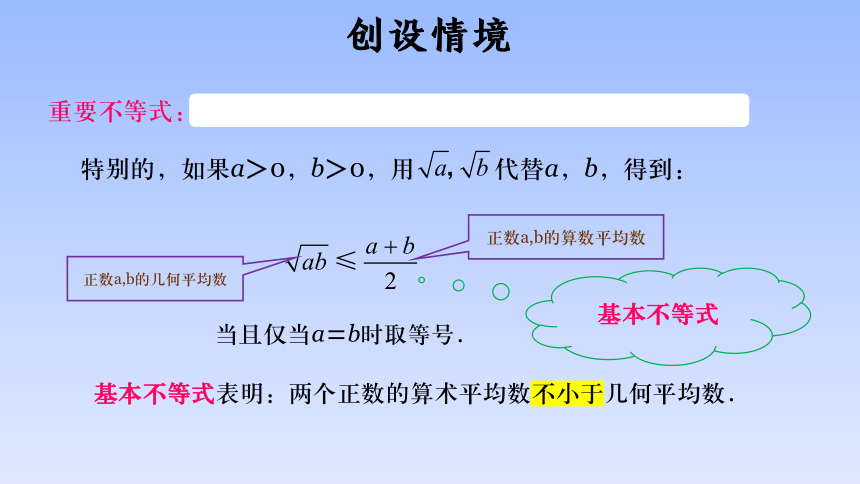
基本不等式表明:两个正数的算术平均数不小于几何平均数.
创设情境
特别的,如果a>0,b>0,用 代替a,b,得到:
当且仅当a=b时取等号.
正数a,b的几何平均数
正数a,b的算数平均数
基本不等式
证: 要证 ①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
要证④,只要证 ⑤
显然,⑤成立,当且仅当 时,⑤中
的等号成立.
证明:
执果索因
分析法
是一种“ ”的证明方法,即从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(定理、定义或公理)为止.
新知探究---熟知特征
分析法的证明格式
一般每一步的推理都用“要证…”“只要证…”的格式,当推导到一个明显成立的条件之后,指出“显然…成立”。
新知探究---熟知特征
同学们,经过从前面基本不等式的代数解释,你是否能联想到从几何角度基本不等式也有背景对应呢?
下面我们一起来探究一下.
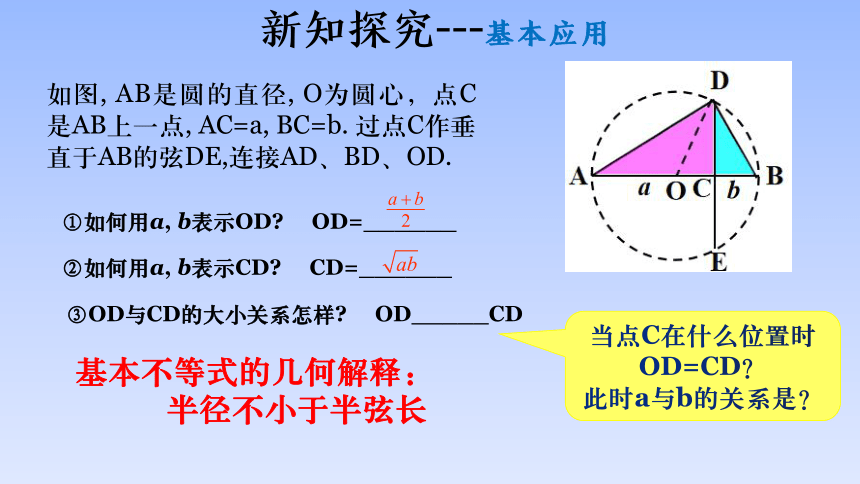
新知探究---基本应用
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
①如何用a, b表示OD OD=______
②如何用a, b表示CD CD=______
③OD与CD的大小关系怎样 OD_____CD
当点C在什么位置时OD=CD?
此时a与b的关系是?
基本不等式的几何解释:
半径不小于半弦长
新知探究---基本应用
例1 若 ,求 的最小值.
解:因为 所以 . 当且仅当 ,即 , 也就是 时 ,等号成立.因此所求最小值为2.
新知探究---综合应用
想一想:
在上述解答过程中,是否必须说明“当且仅当,即时, 等号成立”?
新知探究---技巧方法
这是为了说明“2”是的一个取值.
积定问题
例2 已知x ,y都是正数,求证:
如果积xy 等于定值P,那么当x =y时,和 x +y有最小值 ;
证明:
新知探究---结构认识
和定问题
例2 已知x ,y都是正数,求证:
如果和 x +y等于定值S,那么当x =y时,积xy有最大值 .
证明:
当和x+y等于定值S时, ,所以 .
当且仅当x=y时,上式等号成立.
于是,当x=y时,积xy有最大值 .
新知探究---结构认识
已知x ,y都是正数时,
如果积xy 等于定值P,那么当x =y时,和 x +y有最小值 ;
如果和 x +y等于定值S,那么当x =y时,积xy有最大值 。
归纳:
利用基本不等式求最值,必须按照“一正,二定,三相等”的原则。
新知探究---关键之处
新知检测
如果a>0,那么a+ +2的最小值是( )
A.2 B.2
C.3 D.4
1.基本不等式。即 ,都有 当且仅当 时等号成立;
2.分析法证明基本不等式,利用了不等式的性质;
3. 基本不等式的几何特征.
4.利用基本不等式求代数式的最值。原则是“一正、二定、三相等”。
课堂小结
1、作业本
课本P46第2,5题
2、优化设计 P48-P51
3、优化设计课后训练 P18
作 业
拓展提升
基本不等式(1)
重要不等式: ,a2+b2≥2ab,当且仅当 时,等号成立.
基本不等式表明:两个正数的算术平均数不小于几何平均数.
创设情境
特别的,如果a>0,b>0,用 代替a,b,得到:
当且仅当a=b时取等号.
正数a,b的几何平均数
正数a,b的算数平均数
基本不等式
证: 要证 ①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
要证④,只要证 ⑤
显然,⑤成立,当且仅当 时,⑤中
的等号成立.
证明:
执果索因
分析法
是一种“ ”的证明方法,即从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(定理、定义或公理)为止.
新知探究---熟知特征
分析法的证明格式
一般每一步的推理都用“要证…”“只要证…”的格式,当推导到一个明显成立的条件之后,指出“显然…成立”。
新知探究---熟知特征
同学们,经过从前面基本不等式的代数解释,你是否能联想到从几何角度基本不等式也有背景对应呢?
下面我们一起来探究一下.
新知探究---基本应用
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
①如何用a, b表示OD OD=______
②如何用a, b表示CD CD=______
③OD与CD的大小关系怎样 OD_____CD
当点C在什么位置时OD=CD?
此时a与b的关系是?
基本不等式的几何解释:
半径不小于半弦长
新知探究---基本应用
例1 若 ,求 的最小值.
解:因为 所以 . 当且仅当 ,即 , 也就是 时 ,等号成立.因此所求最小值为2.
新知探究---综合应用
想一想:
在上述解答过程中,是否必须说明“当且仅当,即时, 等号成立”?
新知探究---技巧方法
这是为了说明“2”是的一个取值.
积定问题
例2 已知x ,y都是正数,求证:
如果积xy 等于定值P,那么当x =y时,和 x +y有最小值 ;
证明:
新知探究---结构认识
和定问题
例2 已知x ,y都是正数,求证:
如果和 x +y等于定值S,那么当x =y时,积xy有最大值 .
证明:
当和x+y等于定值S时, ,所以 .
当且仅当x=y时,上式等号成立.
于是,当x=y时,积xy有最大值 .
新知探究---结构认识
已知x ,y都是正数时,
如果积xy 等于定值P,那么当x =y时,和 x +y有最小值 ;
如果和 x +y等于定值S,那么当x =y时,积xy有最大值 。
归纳:
利用基本不等式求最值,必须按照“一正,二定,三相等”的原则。
新知探究---关键之处
新知检测
如果a>0,那么a+ +2的最小值是( )
A.2 B.2
C.3 D.4
1.基本不等式。即 ,都有 当且仅当 时等号成立;
2.分析法证明基本不等式,利用了不等式的性质;
3. 基本不等式的几何特征.
4.利用基本不等式求代数式的最值。原则是“一正、二定、三相等”。
课堂小结
1、作业本
课本P46第2,5题
2、优化设计 P48-P51
3、优化设计课后训练 P18
作 业
拓展提升
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
