2022—2023学年沪科版数学九年级上册23.2 解直角三角形及其应用(3)课件(共16张PPT)
文档属性
| 名称 | 2022—2023学年沪科版数学九年级上册23.2 解直角三角形及其应用(3)课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
23.2 解直角三角形及其应用
第3课时
解直角三角形及其应用
学习目标
准备好了吗?一起去探索吧!
1.加强对坡度、坡角、坡面概念的理解和认识,了解坡度与坡面陡峭程度间的关系.
2.能把一些较复杂的图形转化为解直角三角形的问题.
3.能解决堤坝等关于斜坡的实际问题,提高解决实际问题的能力.
4.在解决问题的过程中感知知识的实际应用,进一步体会数学与实际生活的紧密联系.
知识回顾
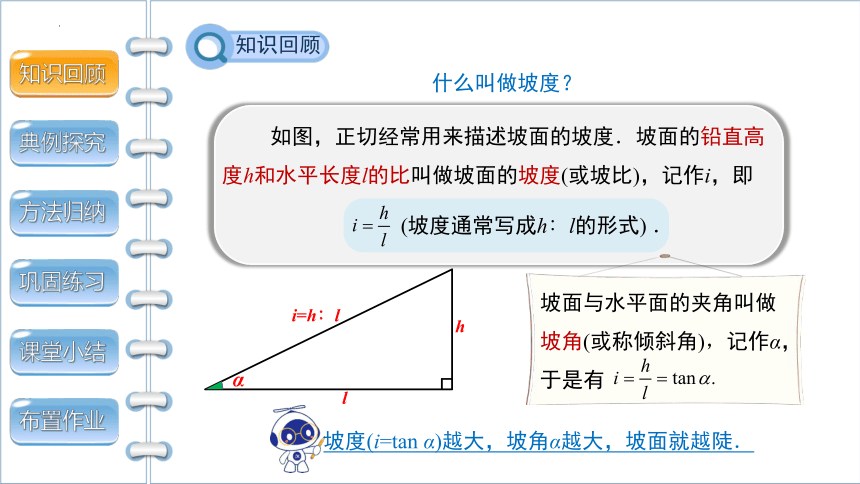
如图,正切经常用来描述坡面的坡度.坡面的铅直高度h和水平长度l的比叫做坡面的坡度(或坡比),记作i,即
i=h∶l
h
l
(坡度通常写成h∶l的形式) .
什么叫做坡度?
坡面与水平面的夹角叫做坡角(或称倾斜角),记作α,于是有
α
坡度(i=tan α)越大,坡角α越大,坡面就越陡.
做一做
如图所示,在△ABC中.
(1)若 h = 2 cm,l = 5 cm,则斜坡AB的坡度 i = ;
(2)若斜坡AB的坡度 i = 1∶1.5,h = 2 m,则 l = ;
(3)若斜坡AB的坡度 i = 1∶2.5,l = 5 m,则 h = .
A
C
B
h
l
1∶2.5
3 m
2 m
知识回顾
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题;(画出平面图形,转化为解直角三角形的问题)
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
做一做
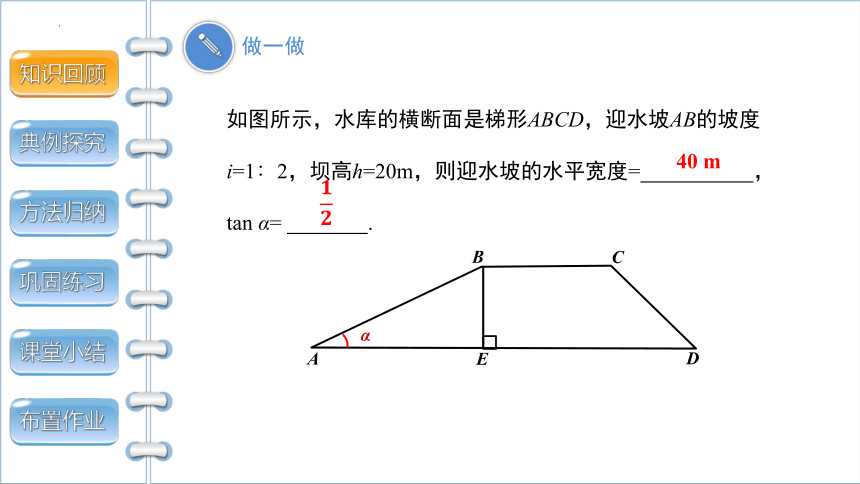
如图所示,水库的横断面是梯形ABCD,迎水坡AB的坡度i=1∶2,坝高h=20m,则迎水坡的水平宽度= ,tan α= .
40 m
A
C
B
α
D
E
A
C
B
α
D
E
β
i=1∶1.6
5.8
i'=1∶2.5
9.8
合作探究
如图,铁路路基的横断面是四边形ABCD,AD∥BC,路基顶宽BC=
9.8 m,路基高BE=5.8 m,斜坡AB的坡度i=1:1.6,斜坡CD的坡度i'=1:2.5,求铁路路基下底宽AD的值(精确到0.1m)与斜坡的坡角α和β(精确到1°)的值。
F
分析:题目中给出了两个坡度值,目前对应的只有一个直角三角形,需要再建立
一个直角三角形;
要计算AD,又有AD=AE+EF+FD,EF=BC=9.8 m,只要再分别求出AE和FD即可;
还要计算坡角α和β,其中坡度与坡角之间的关系是tan α=i=1:1.6,tan β=i'=1:2.5.
A
C
B
α
D
E
β
i=1∶1.6
5.8
i'=1∶2.5
9.8
合作探究
F
解:过点C作CF⊥AD于点F,得
CF=BE,EF=BC,∠A=α,∠D=β.
∵BE=5.8m, = , = ,
∴AE=1.6×5.8=9.28(m),DF=2.5×5.8=14.5(m).
∴AD=AE+EF+DF=9.28+9.8+14.5≈33.6(m).
由tan α=i==0.625,tan β=i'= =0.4,得
α=32°,tan β=22°(可以借助计算器计算).
答:铁路路基下底宽为33.6m,斜坡的坡角分别为32°和22°.
α
方法归纳
利用解直角三角形的知识解决与坡度、坡角有关的实际
问题,特别是与梯形有关的实际问题,懂得通过添加辅助线
把梯形问题转化为直角三角形来解决.
解决与坡度、坡角有关的实际问题
抢答
随堂练习
1.如图,水库的横断面是梯形ABCD,迎水坡AB的坡度i=1∶1,坝高BE=20 m,迎水坡AB=_______m,坡角α=_______.
45°
α
A
C
B
D
E
抢答
随堂练习
2.如图,水库大坝的横断面是四边形ABCD,BC∥AD,坝顶宽为6 m,坝高为23 m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i'=1∶2.5,求:
(1)斜坡AB的坡角α的值(精确到1°);
(2)坝底宽AD和斜坡AB的值(精确到0.1 m).
E
β
A
C
B
α
D
i=1∶3
23
i'=1∶2.5
6
F
分析:根据题意先建立直角三角形;
要计算斜坡AB的坡角α,其中坡度与坡角之间的关系是tan α=i=1:3;
要计算AD,又有AD=AE+EF+FD,EF=BC=6 m,只要再分别求出AE和FD即可;
还要计算AB,在Rt△ABE中求解即可.
抢答
随堂练习
E
β
A
C
B
α
D
i=1∶3
23
i'=1∶2.5
6
F
解:分别过点B、C作垂线,交AD于E、F点,垂足分别为E点、F点,则有
BE=CF=23 m,BC=EF=6 m.
(1)由tan α=i= ,得∠α ≈18°.
(2) ∵BE=CF=23m, = , = ,
∴AE=3×23=69(m),DF=2.5×23=57.5(m).
∴AD=AE+EF+DF=69+6+57.5=132.5(m).
由AE=69 m,BE=23m,根据勾股定理,得AB≈72.7m.
抢答
随堂练习
3.如图,燕尾槽的横断面是四边形ABCD,AD∥BC,其中∠B=∠C=
55°,外口宽AD=180 mm,燕尾槽的深度AE=70 mm,求它的里口宽
BC的值(精确到1 mm)
A
B
D
C
E
解:过点D作垂线,交BC于F点,垂足为F点,则有
AE=DF=70 m,EF=AD=180 mm.
在Rt△ABE中,
BE= = ≈49.01(mm),
∴BC=2BE+EF=49.01×2+180≈278(mm).
答:燕尾槽的里口宽为278 mm.
F
解直角三角形及其应用
坡度(坡比)、坡角、坡面:
解决与坡度、坡角有关的实际问题:
利用解直角三角形的知识解决与坡度、坡角有关的实际问题,特别是与梯形有关的实际问题,懂得通过添加辅助线把梯形问题转化为直角三角形来解决.
坡面的铅直高度h和水平长度l的比叫做坡面的坡度(或坡比),记作i,即
(坡度通常写成h∶l的形式) .
注意:坡度(i=tan α)越大,坡角α越大,坡面就越陡.
教科书第131页习题23.2
第5、6题
再见
23.2 解直角三角形及其应用
第3课时
解直角三角形及其应用
学习目标
准备好了吗?一起去探索吧!
1.加强对坡度、坡角、坡面概念的理解和认识,了解坡度与坡面陡峭程度间的关系.
2.能把一些较复杂的图形转化为解直角三角形的问题.
3.能解决堤坝等关于斜坡的实际问题,提高解决实际问题的能力.
4.在解决问题的过程中感知知识的实际应用,进一步体会数学与实际生活的紧密联系.
知识回顾
如图,正切经常用来描述坡面的坡度.坡面的铅直高度h和水平长度l的比叫做坡面的坡度(或坡比),记作i,即
i=h∶l
h
l
(坡度通常写成h∶l的形式) .
什么叫做坡度?
坡面与水平面的夹角叫做坡角(或称倾斜角),记作α,于是有
α
坡度(i=tan α)越大,坡角α越大,坡面就越陡.
做一做
如图所示,在△ABC中.
(1)若 h = 2 cm,l = 5 cm,则斜坡AB的坡度 i = ;
(2)若斜坡AB的坡度 i = 1∶1.5,h = 2 m,则 l = ;
(3)若斜坡AB的坡度 i = 1∶2.5,l = 5 m,则 h = .
A
C
B
h
l
1∶2.5
3 m
2 m
知识回顾
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题;(画出平面图形,转化为解直角三角形的问题)
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
做一做
如图所示,水库的横断面是梯形ABCD,迎水坡AB的坡度i=1∶2,坝高h=20m,则迎水坡的水平宽度= ,tan α= .
40 m
A
C
B
α
D
E
A
C
B
α
D
E
β
i=1∶1.6
5.8
i'=1∶2.5
9.8
合作探究
如图,铁路路基的横断面是四边形ABCD,AD∥BC,路基顶宽BC=
9.8 m,路基高BE=5.8 m,斜坡AB的坡度i=1:1.6,斜坡CD的坡度i'=1:2.5,求铁路路基下底宽AD的值(精确到0.1m)与斜坡的坡角α和β(精确到1°)的值。
F
分析:题目中给出了两个坡度值,目前对应的只有一个直角三角形,需要再建立
一个直角三角形;
要计算AD,又有AD=AE+EF+FD,EF=BC=9.8 m,只要再分别求出AE和FD即可;
还要计算坡角α和β,其中坡度与坡角之间的关系是tan α=i=1:1.6,tan β=i'=1:2.5.
A
C
B
α
D
E
β
i=1∶1.6
5.8
i'=1∶2.5
9.8
合作探究
F
解:过点C作CF⊥AD于点F,得
CF=BE,EF=BC,∠A=α,∠D=β.
∵BE=5.8m, = , = ,
∴AE=1.6×5.8=9.28(m),DF=2.5×5.8=14.5(m).
∴AD=AE+EF+DF=9.28+9.8+14.5≈33.6(m).
由tan α=i==0.625,tan β=i'= =0.4,得
α=32°,tan β=22°(可以借助计算器计算).
答:铁路路基下底宽为33.6m,斜坡的坡角分别为32°和22°.
α
方法归纳
利用解直角三角形的知识解决与坡度、坡角有关的实际
问题,特别是与梯形有关的实际问题,懂得通过添加辅助线
把梯形问题转化为直角三角形来解决.
解决与坡度、坡角有关的实际问题
抢答
随堂练习
1.如图,水库的横断面是梯形ABCD,迎水坡AB的坡度i=1∶1,坝高BE=20 m,迎水坡AB=_______m,坡角α=_______.
45°
α
A
C
B
D
E
抢答
随堂练习
2.如图,水库大坝的横断面是四边形ABCD,BC∥AD,坝顶宽为6 m,坝高为23 m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i'=1∶2.5,求:
(1)斜坡AB的坡角α的值(精确到1°);
(2)坝底宽AD和斜坡AB的值(精确到0.1 m).
E
β
A
C
B
α
D
i=1∶3
23
i'=1∶2.5
6
F
分析:根据题意先建立直角三角形;
要计算斜坡AB的坡角α,其中坡度与坡角之间的关系是tan α=i=1:3;
要计算AD,又有AD=AE+EF+FD,EF=BC=6 m,只要再分别求出AE和FD即可;
还要计算AB,在Rt△ABE中求解即可.
抢答
随堂练习
E
β
A
C
B
α
D
i=1∶3
23
i'=1∶2.5
6
F
解:分别过点B、C作垂线,交AD于E、F点,垂足分别为E点、F点,则有
BE=CF=23 m,BC=EF=6 m.
(1)由tan α=i= ,得∠α ≈18°.
(2) ∵BE=CF=23m, = , = ,
∴AE=3×23=69(m),DF=2.5×23=57.5(m).
∴AD=AE+EF+DF=69+6+57.5=132.5(m).
由AE=69 m,BE=23m,根据勾股定理,得AB≈72.7m.
抢答
随堂练习
3.如图,燕尾槽的横断面是四边形ABCD,AD∥BC,其中∠B=∠C=
55°,外口宽AD=180 mm,燕尾槽的深度AE=70 mm,求它的里口宽
BC的值(精确到1 mm)
A
B
D
C
E
解:过点D作垂线,交BC于F点,垂足为F点,则有
AE=DF=70 m,EF=AD=180 mm.
在Rt△ABE中,
BE= = ≈49.01(mm),
∴BC=2BE+EF=49.01×2+180≈278(mm).
答:燕尾槽的里口宽为278 mm.
F
解直角三角形及其应用
坡度(坡比)、坡角、坡面:
解决与坡度、坡角有关的实际问题:
利用解直角三角形的知识解决与坡度、坡角有关的实际问题,特别是与梯形有关的实际问题,懂得通过添加辅助线把梯形问题转化为直角三角形来解决.
坡面的铅直高度h和水平长度l的比叫做坡面的坡度(或坡比),记作i,即
(坡度通常写成h∶l的形式) .
注意:坡度(i=tan α)越大,坡角α越大,坡面就越陡.
教科书第131页习题23.2
第5、6题
再见
