2022—2023学年沪科版数学九年级上册23.2 解直角三角形及其应用(4)课件(共13张PPT)
文档属性
| 名称 | 2022—2023学年沪科版数学九年级上册23.2 解直角三角形及其应用(4)课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1009.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 21:01:54 | ||
图片预览



文档简介
(共13张PPT)
23.2 解直角三角形及其应用
第4课时
解直角三角形及其应用
学习目标
准备好了吗?一起去探索吧!
1.进一步巩固解直角三角形的应用.
2.了解直线的向上方向与x轴正方向夹角的正切值与直线一次项系数
k之间的关系.
3.能用解直角三角形的知识灵活解决与直线相关的问题.
4.在解决问题的过程中感知知识的实际应用,培养学生的应用意识.
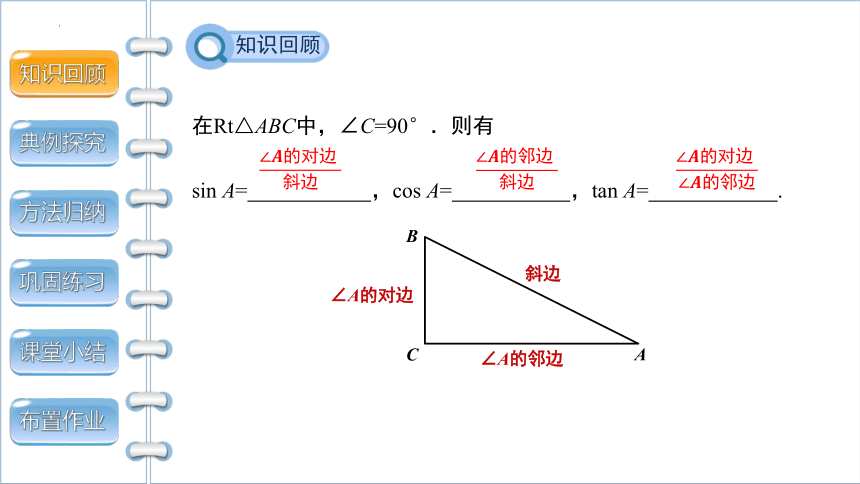
知识回顾
在Rt△ABC中,∠C=90°.则有
sin A= ,cos A= ,tan A= .
A
C
B
∠A的对边
∠A的邻边
斜边
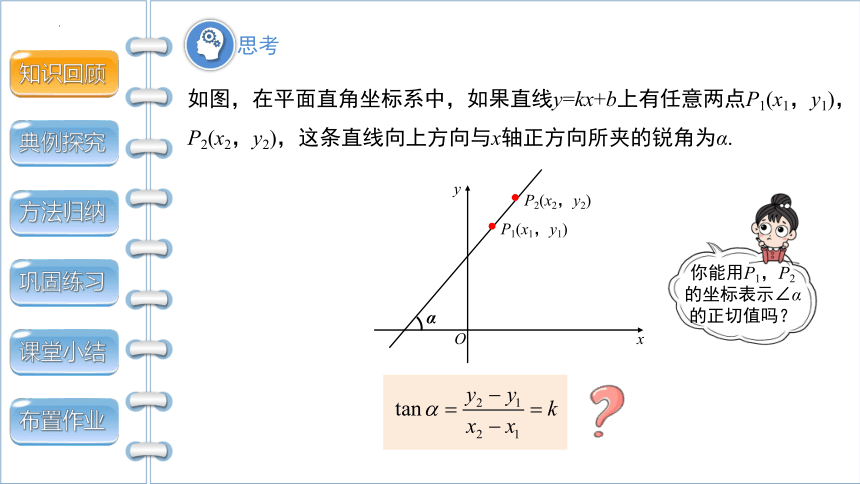
如图,在平面直角坐标系中,如果直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.
O
α
P2(x2,y2)
P1(x1,y1)
x
y
思考
你能用P1,P2的坐标表示∠α的正切值吗?
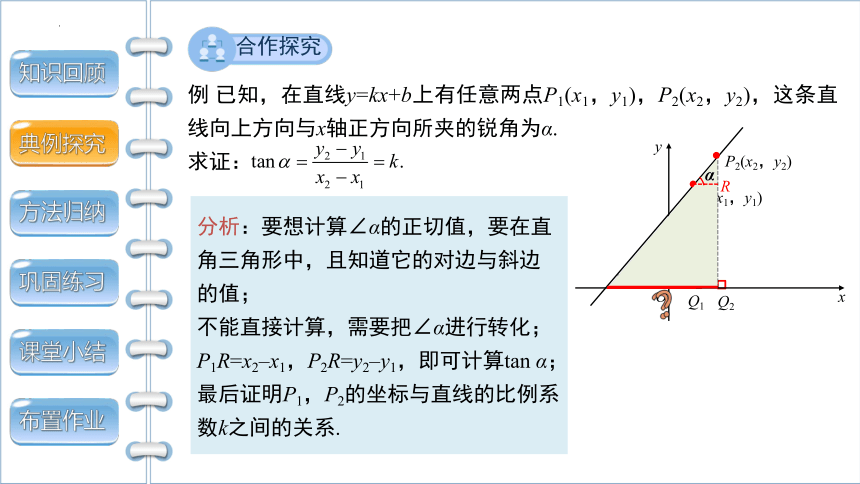
合作探究
例 已知,在直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.
求证:
O
α
P2(x2,y2)
P1(x1,y1)
x
y
分析:要想计算∠α的正切值,要在直
角三角形中,且知道它的对边与斜边
的值;
不能直接计算,需要把∠α进行转化;
P1R=x2–x1,P2R=y2–y1,即可计算tan α;
最后证明P1,P2的坐标与直线的比例系
数k之间的关系.
Q1
Q2
α
R
合作探究
证明:如图,由α是锐角,可知直线y=kx+b是上升的,即函数y=kx+b的值随x值的增大而增大.
设x1<x2,则y1<y2.过点P1,P2的作x轴的垂线,
垂足分别为Q1,Q2,再过点P1作x轴的平行线
P1R交P2Q2于点R,得
∠P2P1R=α.
在Rt△P2P1R中,
O
α
P2(x2,y2)
P1(x1,y1)
x
y
Q1
Q2
α
R
∵P1,P2都在直线y=kx+b上,
∴y1=kx1+b①, y2=kx2+b②.
由② – ①,得y2–y1=k(x2–x1),
例 已知,在直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.
求证:
方法归纳
如果直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.那么我们可以得到如下结论:
O
α
P2(x2,y2)
P1(x1,y1)
x
y
抢答
随堂练习
1.如图,直线y=2x+1向上的方向与x轴的正方向所夹的锐角为α.那么
(1)tan α= ;(2) sin α= ;(3) cos α= .
O
α
x
y
2
抢答
随堂练习
O
α
x
y
P
2.在平面直角坐标系的第一象限中,有一点P(x,y),记r=|OP|=.
若OP与x轴正方向所夹的锐角为α,则
(1)sin α= ;(2) cos α= ;(3) tan α= .
y
x
抢答
随堂练习
3.已知直线l的向上方向与x轴正方向的夹角是一个锐角α,且sin α=.
求直线l的比例系数.
解:设直线l的比例系数为k.
∵sin α = ,
∴tan α = .
∴直线l的比例系数k的值为.
解直角三角形及其应用
如果直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.那么我们可以得到如下结论:
O
α
P2(x2,y2)
P1(x1,y1)
x
y
教科书第130页练习
再见
23.2 解直角三角形及其应用
第4课时
解直角三角形及其应用
学习目标
准备好了吗?一起去探索吧!
1.进一步巩固解直角三角形的应用.
2.了解直线的向上方向与x轴正方向夹角的正切值与直线一次项系数
k之间的关系.
3.能用解直角三角形的知识灵活解决与直线相关的问题.
4.在解决问题的过程中感知知识的实际应用,培养学生的应用意识.
知识回顾
在Rt△ABC中,∠C=90°.则有
sin A= ,cos A= ,tan A= .
A
C
B
∠A的对边
∠A的邻边
斜边
如图,在平面直角坐标系中,如果直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.
O
α
P2(x2,y2)
P1(x1,y1)
x
y
思考
你能用P1,P2的坐标表示∠α的正切值吗?
合作探究
例 已知,在直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.
求证:
O
α
P2(x2,y2)
P1(x1,y1)
x
y
分析:要想计算∠α的正切值,要在直
角三角形中,且知道它的对边与斜边
的值;
不能直接计算,需要把∠α进行转化;
P1R=x2–x1,P2R=y2–y1,即可计算tan α;
最后证明P1,P2的坐标与直线的比例系
数k之间的关系.
Q1
Q2
α
R
合作探究
证明:如图,由α是锐角,可知直线y=kx+b是上升的,即函数y=kx+b的值随x值的增大而增大.
设x1<x2,则y1<y2.过点P1,P2的作x轴的垂线,
垂足分别为Q1,Q2,再过点P1作x轴的平行线
P1R交P2Q2于点R,得
∠P2P1R=α.
在Rt△P2P1R中,
O
α
P2(x2,y2)
P1(x1,y1)
x
y
Q1
Q2
α
R
∵P1,P2都在直线y=kx+b上,
∴y1=kx1+b①, y2=kx2+b②.
由② – ①,得y2–y1=k(x2–x1),
例 已知,在直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.
求证:
方法归纳
如果直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.那么我们可以得到如下结论:
O
α
P2(x2,y2)
P1(x1,y1)
x
y
抢答
随堂练习
1.如图,直线y=2x+1向上的方向与x轴的正方向所夹的锐角为α.那么
(1)tan α= ;(2) sin α= ;(3) cos α= .
O
α
x
y
2
抢答
随堂练习
O
α
x
y
P
2.在平面直角坐标系的第一象限中,有一点P(x,y),记r=|OP|=.
若OP与x轴正方向所夹的锐角为α,则
(1)sin α= ;(2) cos α= ;(3) tan α= .
y
x
抢答
随堂练习
3.已知直线l的向上方向与x轴正方向的夹角是一个锐角α,且sin α=.
求直线l的比例系数.
解:设直线l的比例系数为k.
∵sin α = ,
∴tan α = .
∴直线l的比例系数k的值为.
解直角三角形及其应用
如果直线y=kx+b上有任意两点P1(x1,y1),P2(x2,y2),这条直线向上方向与x轴正方向所夹的锐角为α.那么我们可以得到如下结论:
O
α
P2(x2,y2)
P1(x1,y1)
x
y
教科书第130页练习
再见
