2022—2023学年沪科版数学九年级上册23.2 解直角三角形及其应用(1)课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年沪科版数学九年级上册23.2 解直角三角形及其应用(1)课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 21:02:42 | ||
图片预览





文档简介
(共17张PPT)
23.2 解直角三角形及其应用
第1课时
学习目标
解直角三角形
准备好了吗?一起去探索吧!
1.理解直角三角形中,除直角外其余五个元素之间的关系.
2.会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
3.通过综合运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
4.渗透数形结合的数学思想,培养学生良好的学习习惯.
情境引入
某电视塔如右图所示,已知塔尖距离地面的高度AB是240米.现要从塔尖向地面点C处拉一根线,如果测得塔底的中心到点C的距离是100米,那么你能帮着计算一下AC的长度吗?
A
B
C
观察
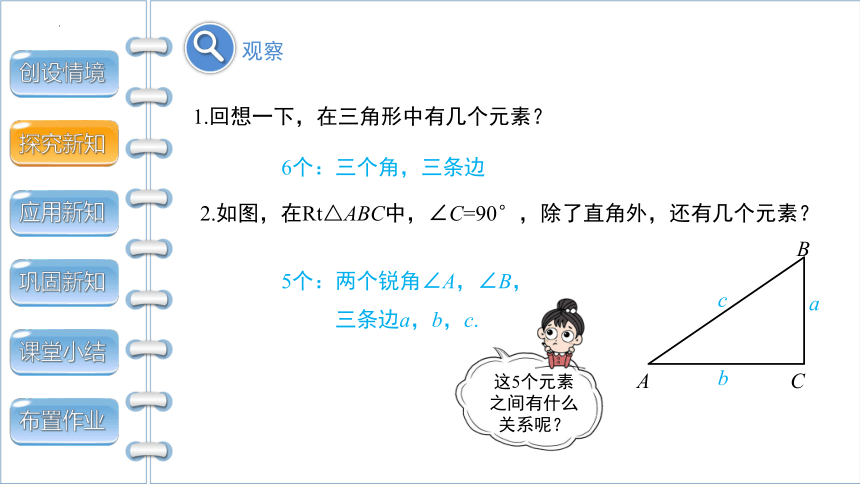
1.回想一下,在三角形中有几个元素?
6个:三个角,三条边
2.如图,在Rt△ABC中,∠C=90°,除了直角外,还有几个元素?
A
B
C
5个:两个锐角∠A,∠B,
三条边a,b,c.
这5个元素之间有什么关系呢?
a
b
c
观察
a2+b2=c2
如图,在Rt△ABC中,除了直角(∠C)外,其它5个元素之间有什么关系呢?
∠A+∠B=90°
A
B
C
a
b
c
(1)三边之间的关系:
(2)两个锐角之间的关系:
(3)边角之间的关系:
sin A= ,cos A= ,tan A= .
sin B= ,cos B= ,tan B= .
对于锐角B,也有类似的边角关系吗?
观察
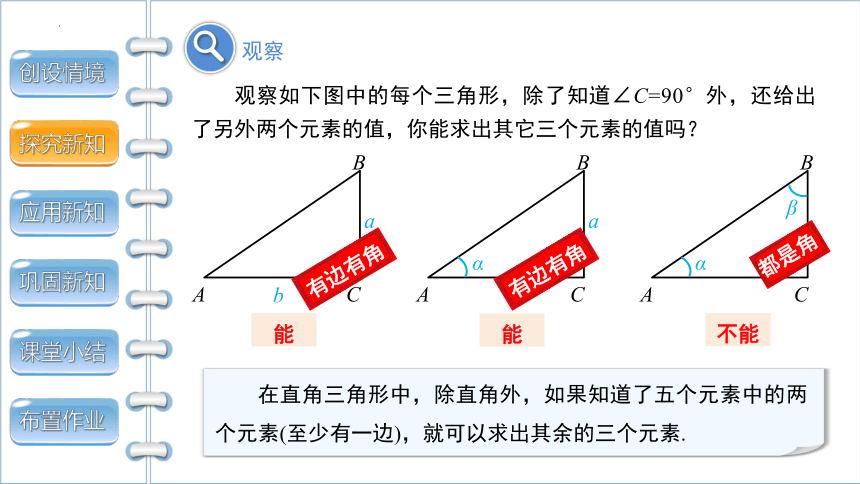
观察如下图中的每个三角形,除了知道∠C=90°外,还给出了另外两个元素的值,你能求出其它三个元素的值吗?
A
B
C
a
b
A
B
C
a
A
B
C
α
α
β
能
能
不能
在直角三角形中,除直角外,如果知道了五个元素中的两个元素(至少有一边),就可以求出其余的三个元素.
都是角
有边有角
有边有角
归纳
A
B
C
a
b
c
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
条件:①在直角三角形中;
②知道除直角外的至少两个元素;
③至少有一个元素是边.
思考
1.解直角三角形的条件是什么?
除直角外的两个元素(至少有一边)
2.解直角三角形的依据是什么?
a2+b2=c2
∠A+∠B=90°
(1)三边之间的关系:
(2)两个锐角之间的关系:
(3)边角之间的关系:
sin A= ,cos A= ,tan A= .
sin B= ,cos B= ,tan B= .
A
B
C
a
b
c
勾股定理
两锐角互余
锐角三角函数
典型例题
例1 在Rt△ABC中,∠C=90°,∠B=42°6',c=287.4,解这个直角三角形(精确到0.1).
B
A
C
b
a
c
分析:
已知:∠C=90°,∠B=42°6',c=287.4.
未知:∠A,a,b.
287.4
解:由cos B=,得a=c cos B=287.4×0.7420≈213.3.
由sin B=,得b=c sin B=287.4×0.6704≈192.7.
213.3
192.7
∠A=90°–∠B=90°–42°6'=47°54'.
典型例题
例2 在△ABC中,∠A=55°,b=20 cm,c=30 cm,求三角形的面积S△ABC(精确到0.1 cm2).
B
A
C
分析:目前图中没有直角三角形,因此要根据题意作出直角三角形.
D
55°
20 cm
30 cm
要计算的是S△ABC,只要再计算得到CD(△ABC中AB边上的高)的长即可.
典型例题
例2 在△ABC中,∠A=55°,b=20 cm,c=30 cm,求三角形的面积S△ABC(精确到0.1 cm2).
B
A
C
D
55°
20 cm
30 cm
解:如图,作AB上的高CD.在Rt△ACD中,
∵CD=AC·sin A=b·sin A,
∴ S△ABC=AB·CD=bc sin A.
当∠A=55°,b=20 cm,c=30 cm时,有
S△ABC=bc sin A= 20×30 sin55°
= 20×30×0.8192
≈245.8(cm2).
三角形的面积等于一组邻边与其夹角正弦值积的一半.
抢答
随堂练习
1.选择题.
(1)在下列直角三角形中,不能求解的是 ( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
(2)在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
D
抢答
随堂练习
2.填空题.
在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=_____.
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75).
24
抢答
随堂练习
3.在 Rt△ABC 中,∠C=90°,∠B=72°,c = 14.
根据条件解直角三角形.
( 参考数据: )
A
B
C
b
a
c
解:∠A=90°–∠B=90°–72°=18°.
解直角三角形
解直角三角形:
解直角三角形的依据:
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
条件:①在直角三角形中;
②知道除直角外的至少两个元素;
③至少有一个元素是边.
勾股定理
两锐角互余
锐角三角函数
教科书第125页练习
第1、2、3题
再见
23.2 解直角三角形及其应用
第1课时
学习目标
解直角三角形
准备好了吗?一起去探索吧!
1.理解直角三角形中,除直角外其余五个元素之间的关系.
2.会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
3.通过综合运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
4.渗透数形结合的数学思想,培养学生良好的学习习惯.
情境引入
某电视塔如右图所示,已知塔尖距离地面的高度AB是240米.现要从塔尖向地面点C处拉一根线,如果测得塔底的中心到点C的距离是100米,那么你能帮着计算一下AC的长度吗?
A
B
C
观察
1.回想一下,在三角形中有几个元素?
6个:三个角,三条边
2.如图,在Rt△ABC中,∠C=90°,除了直角外,还有几个元素?
A
B
C
5个:两个锐角∠A,∠B,
三条边a,b,c.
这5个元素之间有什么关系呢?
a
b
c
观察
a2+b2=c2
如图,在Rt△ABC中,除了直角(∠C)外,其它5个元素之间有什么关系呢?
∠A+∠B=90°
A
B
C
a
b
c
(1)三边之间的关系:
(2)两个锐角之间的关系:
(3)边角之间的关系:
sin A= ,cos A= ,tan A= .
sin B= ,cos B= ,tan B= .
对于锐角B,也有类似的边角关系吗?
观察
观察如下图中的每个三角形,除了知道∠C=90°外,还给出了另外两个元素的值,你能求出其它三个元素的值吗?
A
B
C
a
b
A
B
C
a
A
B
C
α
α
β
能
能
不能
在直角三角形中,除直角外,如果知道了五个元素中的两个元素(至少有一边),就可以求出其余的三个元素.
都是角
有边有角
有边有角
归纳
A
B
C
a
b
c
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
条件:①在直角三角形中;
②知道除直角外的至少两个元素;
③至少有一个元素是边.
思考
1.解直角三角形的条件是什么?
除直角外的两个元素(至少有一边)
2.解直角三角形的依据是什么?
a2+b2=c2
∠A+∠B=90°
(1)三边之间的关系:
(2)两个锐角之间的关系:
(3)边角之间的关系:
sin A= ,cos A= ,tan A= .
sin B= ,cos B= ,tan B= .
A
B
C
a
b
c
勾股定理
两锐角互余
锐角三角函数
典型例题
例1 在Rt△ABC中,∠C=90°,∠B=42°6',c=287.4,解这个直角三角形(精确到0.1).
B
A
C
b
a
c
分析:
已知:∠C=90°,∠B=42°6',c=287.4.
未知:∠A,a,b.
287.4
解:由cos B=,得a=c cos B=287.4×0.7420≈213.3.
由sin B=,得b=c sin B=287.4×0.6704≈192.7.
213.3
192.7
∠A=90°–∠B=90°–42°6'=47°54'.
典型例题
例2 在△ABC中,∠A=55°,b=20 cm,c=30 cm,求三角形的面积S△ABC(精确到0.1 cm2).
B
A
C
分析:目前图中没有直角三角形,因此要根据题意作出直角三角形.
D
55°
20 cm
30 cm
要计算的是S△ABC,只要再计算得到CD(△ABC中AB边上的高)的长即可.
典型例题
例2 在△ABC中,∠A=55°,b=20 cm,c=30 cm,求三角形的面积S△ABC(精确到0.1 cm2).
B
A
C
D
55°
20 cm
30 cm
解:如图,作AB上的高CD.在Rt△ACD中,
∵CD=AC·sin A=b·sin A,
∴ S△ABC=AB·CD=bc sin A.
当∠A=55°,b=20 cm,c=30 cm时,有
S△ABC=bc sin A= 20×30 sin55°
= 20×30×0.8192
≈245.8(cm2).
三角形的面积等于一组邻边与其夹角正弦值积的一半.
抢答
随堂练习
1.选择题.
(1)在下列直角三角形中,不能求解的是 ( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
(2)在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
D
抢答
随堂练习
2.填空题.
在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=_____.
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75).
24
抢答
随堂练习
3.在 Rt△ABC 中,∠C=90°,∠B=72°,c = 14.
根据条件解直角三角形.
( 参考数据: )
A
B
C
b
a
c
解:∠A=90°–∠B=90°–72°=18°.
解直角三角形
解直角三角形:
解直角三角形的依据:
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
条件:①在直角三角形中;
②知道除直角外的至少两个元素;
③至少有一个元素是边.
勾股定理
两锐角互余
锐角三角函数
教科书第125页练习
第1、2、3题
再见
