数学人教A版(2019)选择性必修第一册2.3.1点到直线的距离公式(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.1点到直线的距离公式(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 20:19:52 | ||
图片预览






文档简介
(共21张PPT)
2.3.3点到直线的距离公式
教学目标:探索并掌握平面上点到直线的距离公式
教学重点:点到直线距离公式的应用.
教学难点:点到直线距离公式的推导过程.
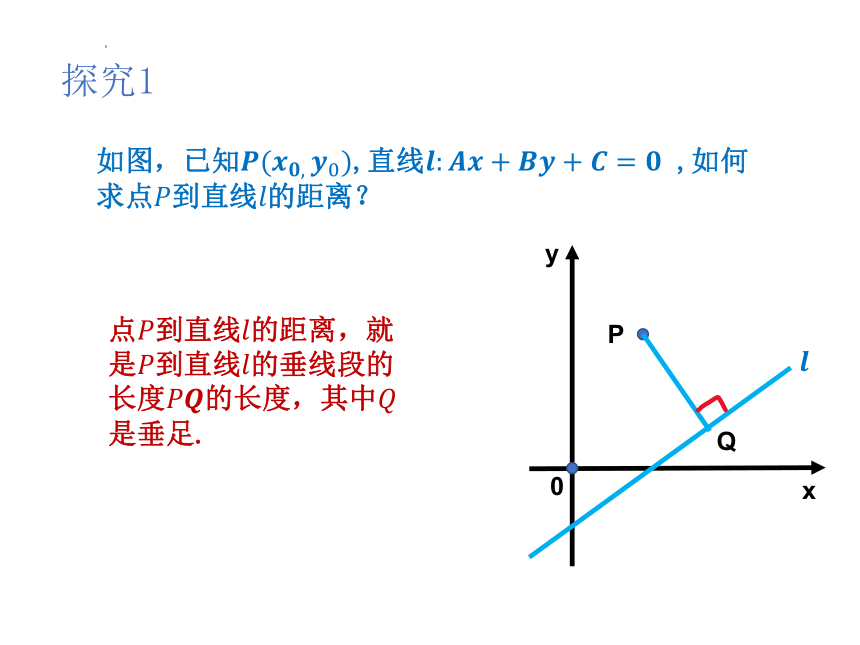
如图,已知,直线 ,如何求点到直线的距离?
探究1
x
0
y
P
Q
点到直线的距离,就是到直线的垂线段的长度的长度,其中是垂足.
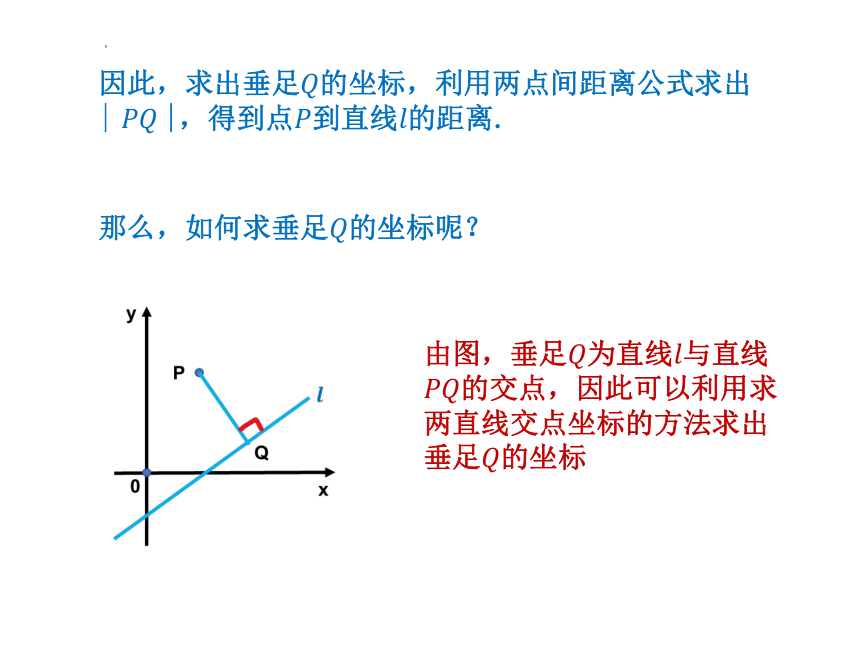
因此,求出垂足的坐标,利用两点间距离公式求出| |,得到点到直线的距离.
那么,如何求垂足的坐标呢?
由图,垂足为直线与直线的交点,因此可以利用求两直线交点坐标的方法求出垂足的坐标
当0,0.由,以及直线的斜率为,可得直线的垂线的斜率为
求垂足Q的坐标:
因此,垂线的方程为即
解方程组
求垂足Q的坐标:
因此,可得直线与的交点坐标,即垂足的坐标为
×, ×可得:
解得:
×, ×可得:
解得:
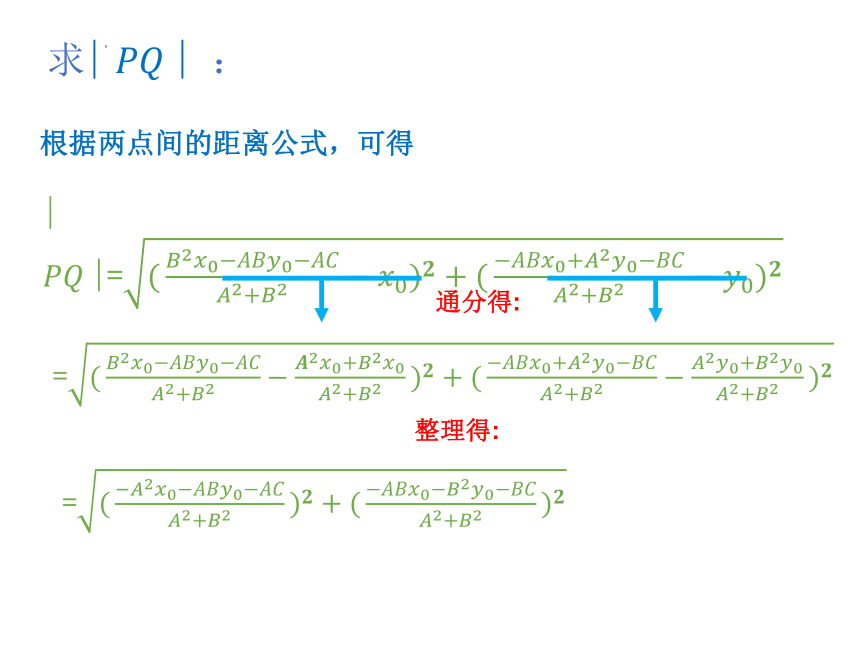
根据两点间的距离公式,可得
求| | :
| |=
通分得:
=
整理得:
=
整理得:
求| | :
因此,点到直线 的距离
| |=
可以验证,当0,或0时,上述公式仍然成立
当0,0时,直线:
即:
当0,0. 直线距离满足吗?
x
0
y
P
Q
追问1:
此时:可得点
| |=| |=| |
=
当0,0时,直线:
即:
当0,0. 直线距离满足吗?
x
0
y
P
Q
追问2:
此时:可得点
| |=||=| |
=
因此,可以验证,当0,或0时,点到直线 的距离公式
仍然成立
我们知道,向量是解决距离、角度问题的有力工具,能否用向量的方法求点到直线的距离?
探究2
x
0
y
P
Q
点到直线的距离,就是向量的模
设是直线上的任意一点, 是与直线的方向向量垂直的单位向量,
则是在上的投影向量,
即
所以| |
求|关键是求,那么如何利用直线
得到呢?
求向量( 是与直线的方向向量垂直的单位向量)
设 是直线 上的任意两点,则=( - , - )是直线的方向向量.
设 是直线 上的任意两点,则有
, ,两式相减 得:
由平面向量的数量积运算可知,向量( , )与向量( - , - )垂直,因此( , )就是与直线的方向向量垂直的单位向量
取= ( , ),从而
向量法求| | :
=
=( - , - ) ( , )
=
=
因为点在直线上,所以.
所以,代入上式,得
| |=| |=
总结:
比较上述两种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;第二种方法利用向量投影,通过向量运算求出结果,简化了运算
解:点P(-1,2)到直线的距离
例1:求点P(-1,2)到直线的距离.
解:如图,设边上的高为h,则
S = | |h
| |=
例2:已知的三个顶点分别是(1,3)(3,1)(-1,0),求的面积.
例2:已知的三个顶点分别是(1,3)(3,1)(-1,0),求的面积.
点C到直线AB的距离h=
因此, S = × 5
边AB所在直线的方程为 ,
即
边AB上的高h就是点C到直线AB的距离
练习
1.求原点到下列直线的距离
(1)
(2)
2.求下列点到直线的距离
(1)
(2)
(3)
3.已知点到直线 的距离为1,求C的值
谢谢
2.3.3点到直线的距离公式
教学目标:探索并掌握平面上点到直线的距离公式
教学重点:点到直线距离公式的应用.
教学难点:点到直线距离公式的推导过程.
如图,已知,直线 ,如何求点到直线的距离?
探究1
x
0
y
P
Q
点到直线的距离,就是到直线的垂线段的长度的长度,其中是垂足.
因此,求出垂足的坐标,利用两点间距离公式求出| |,得到点到直线的距离.
那么,如何求垂足的坐标呢?
由图,垂足为直线与直线的交点,因此可以利用求两直线交点坐标的方法求出垂足的坐标
当0,0.由,以及直线的斜率为,可得直线的垂线的斜率为
求垂足Q的坐标:
因此,垂线的方程为即
解方程组
求垂足Q的坐标:
因此,可得直线与的交点坐标,即垂足的坐标为
×, ×可得:
解得:
×, ×可得:
解得:
根据两点间的距离公式,可得
求| | :
| |=
通分得:
=
整理得:
=
整理得:
求| | :
因此,点到直线 的距离
| |=
可以验证,当0,或0时,上述公式仍然成立
当0,0时,直线:
即:
当0,0. 直线距离满足吗?
x
0
y
P
Q
追问1:
此时:可得点
| |=| |=| |
=
当0,0时,直线:
即:
当0,0. 直线距离满足吗?
x
0
y
P
Q
追问2:
此时:可得点
| |=||=| |
=
因此,可以验证,当0,或0时,点到直线 的距离公式
仍然成立
我们知道,向量是解决距离、角度问题的有力工具,能否用向量的方法求点到直线的距离?
探究2
x
0
y
P
Q
点到直线的距离,就是向量的模
设是直线上的任意一点, 是与直线的方向向量垂直的单位向量,
则是在上的投影向量,
即
所以| |
求|关键是求,那么如何利用直线
得到呢?
求向量( 是与直线的方向向量垂直的单位向量)
设 是直线 上的任意两点,则=( - , - )是直线的方向向量.
设 是直线 上的任意两点,则有
, ,两式相减 得:
由平面向量的数量积运算可知,向量( , )与向量( - , - )垂直,因此( , )就是与直线的方向向量垂直的单位向量
取= ( , ),从而
向量法求| | :
=
=( - , - ) ( , )
=
=
因为点在直线上,所以.
所以,代入上式,得
| |=| |=
总结:
比较上述两种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;第二种方法利用向量投影,通过向量运算求出结果,简化了运算
解:点P(-1,2)到直线的距离
例1:求点P(-1,2)到直线的距离.
解:如图,设边上的高为h,则
S = | |h
| |=
例2:已知的三个顶点分别是(1,3)(3,1)(-1,0),求的面积.
例2:已知的三个顶点分别是(1,3)(3,1)(-1,0),求的面积.
点C到直线AB的距离h=
因此, S = × 5
边AB所在直线的方程为 ,
即
边AB上的高h就是点C到直线AB的距离
练习
1.求原点到下列直线的距离
(1)
(2)
2.求下列点到直线的距离
(1)
(2)
(3)
3.已知点到直线 的距离为1,求C的值
谢谢
