高中数学人教A版(2019)选择性必修第一册单元测试卷第一章B卷(含解析)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册单元测试卷第一章B卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 21:06:34 | ||
图片预览




文档简介
一、单选题
1.已知正四棱台的上、下底面边长分别为1和2,P是上底面的边界上一点.若的最小值为,则该正四棱台的体积为( )
A. B.3 C. D.1
2.已知长方体,,,M是的中点,点P满足,其中,,且平面,则动点P的轨迹所形成的轨迹长度是( )
A. B. C. D.2
3.如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为,腰为3的等腰三角形,则该几何体的体积为( )
A.23 B.24 C.26 D.27
4.已知函数的定义域为,值域为,则的取值范围是( )
A. B.
C. D.
5.向量的运算包含点乘和叉乘,其中点乘就是大家熟悉的向量的数量积.现定义向量的叉乘:给定两个不共线的空间向量与,规定:①为同时与,垂直的向量;②,,三个向量构成右手系(如图1);③;④若,,则,其中.如图2,在长方体中,,,则下列结论正确的是( )
A.
B.
C.
D.长方体的体积
6.如图,四边形中,.现将沿折起,当二面角处于过程中,直线与所成角的余弦值取值范围是( )
A. B. C. D.
7.已知正方体的外接球表面积为,点E为棱的中点,且平面,点平面,则平面截正方体所得的截面图形的面积为( )
A. B. C. D.
8.已知不共线的平面向量两两所成的角相等,且,则( )
A. B.2 C.3 D.2或3
二、多选题
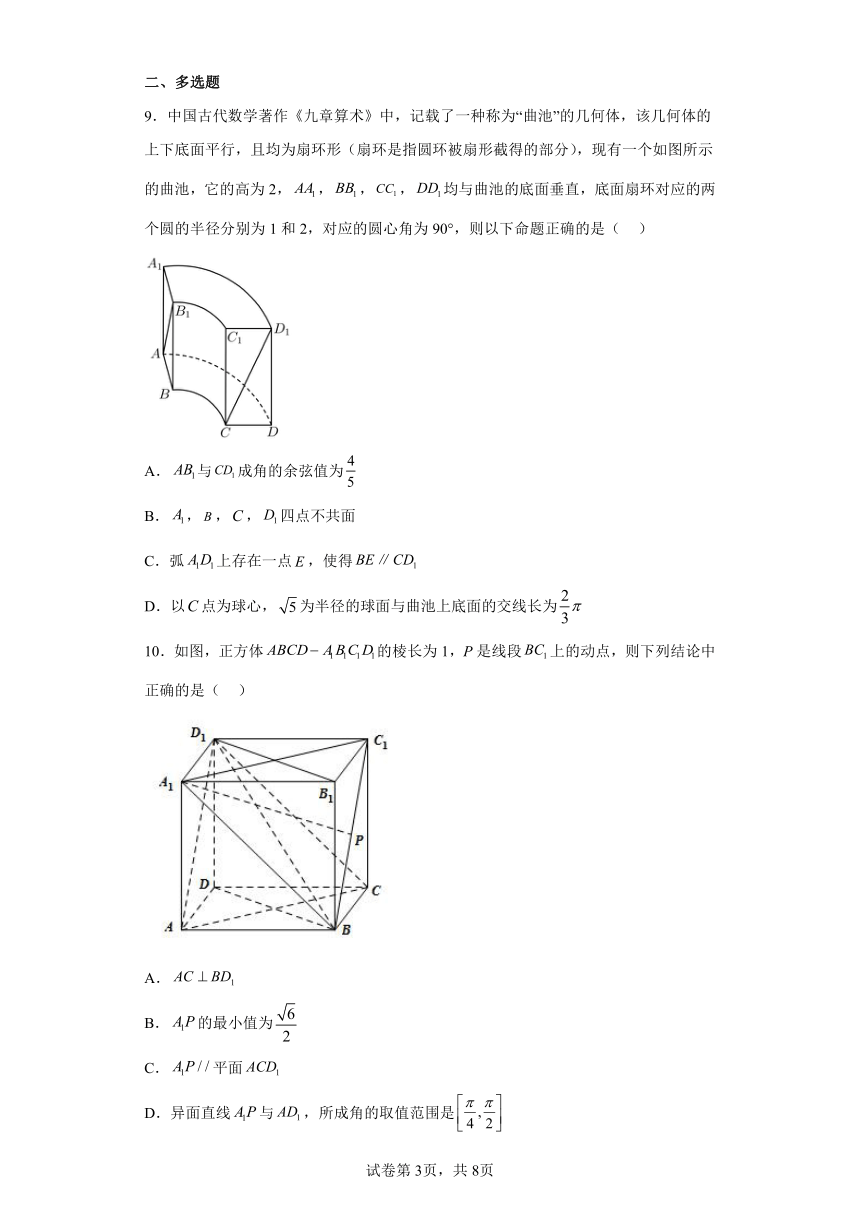
9.中国古代数学著作《九章算术》中,记载了一种称为“曲池”的几何体,该几何体的上下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分),现有一个如图所示的曲池,它的高为2,,,,均与曲池的底面垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为90°,则以下命题正确的是( )
A.与成角的余弦值为
B.,,,四点不共面
C.弧上存在一点,使得
D.以点为球心,为半径的球面与曲池上底面的交线长为
10.如图,正方体的棱长为1,P是线段上的动点,则下列结论中正确的是( )
A.
B.的最小值为
C.平面
D.异面直线与,所成角的取值范围是
11.如图,在直三棱柱中,,,D是棱的中点,,点E在上,且,则下列结论正确的是( )
A.直线与BC所成角为90°
B.三棱锥的体积为
C.平面
D.直三棱柱外接球的表面积为
12.摩天轮常被当作一个城市的地标性建筑,如深圳前海的“湾区之光”摩天轮,如图所示,某摩天轮最高点离地面高度128米,转盘直径为120米,设置若干个座舱,游客从离地面最近的位置进舱,开启后按逆时针匀速旋转分钟,当时,游客随舱旋转至距离地面最远处.以下关于摩天轮的说法中,正确的为( )
A.摩天轮离地面最近的距离为4米
B.若旋转分钟后,游客距离地面的高度为米,则
C.若在,时刻,游客距离地面的高度相等,则的最小值为30
D.,,使得游客在该时刻距离地面的高度均为90米
三、填空题
13.在长方体中,底面是边长为的正方形,,,分别为棱,的中点,为线段上的动点,则直线与平面的交点的轨迹长度为______.
14.在四面体中,棱,,两两垂直,且,,,为的重心,则______.
15.二面角为,A,B是棱l上的两点,,分别在半平面内,,,且,,则的长_______________.
16.如图,边长为的正方形所在平面与正方形所在平面互相垂直,动点、分别在正方形对角线和上移动,且.则下列结论:
①长度的最小值为;
②当时,与相交;
③始终与平面平行;
④当时,为直二面角.
正确的序号是__________.
四、解答题
17.如图,在四棱锥中,平面,.
(1)求A到平面的距离;
(2)求平面与平面夹角的余弦值;
(3)设E为棱上的点,满足异面直线与所成的角为,求的长.
18.如图,在四棱台中,底面四边形ABCD为菱形,平面.
(1)若点是的中点,求证:平面
(2)求直线与平面所成角的余弦值;
(3)棱上存在点,使得,求平面与平面的夹角的正弦值.
19.如图所示的圆柱中,AB是圆O的直径,,为圆柱的母线,四边形ABCD是底面圆O的内接等腰梯形,且,E,F分别为,的中点.
(1)证明:平面ABCD;
(2)求平面与平面所成锐二面角的余弦值.
20.如图,是圆的直径,圆所在的平面,为圆周上一点,为线段的中点,,.
(1)证明:平面平面.
(2)若为的中点,求二面角的余弦值.
21.如图,平面,,,,四边形的对角线交于点M,N为棱上一点,且平面.
(1)求的值:
(2)求二面角的余弦值.
22.如图,在四棱锥P ABCD中,已知AB∥CD,AD⊥CD,BC=BP,CD=2AB=4,△ADP是等边三角形,E为DP的中点.
(1)证明:AE⊥平面PCD;
(2)若,求平面PBC与平面PAD夹角的余弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据题意建立空间直角坐标系,写出相应点的坐标,利用空间向量的数量积的坐标公式及二次函数的性质及已知得出正四棱台的高,
再结合棱台的体积公式即可求解.
【详解】由题意可知,以为坐标原点,所在直线分别为轴,建立空间直角坐标系,如图所示
,,由对称性,点在是相同的,
故只考虑在上时,设正四棱台的高为,则
,,
设,,
因为在上,所以,则
,
,
所以
由二次函数的性质知,当时,取得最小值为,
又因为的最小值为,所以,解得(负舍),
故正四棱台的体积为
.
故选:A.
2.A
【分析】先构造和平面平行的截面,再根据空间向量共面确定点的轨迹形状,再求其长度.
【详解】如图所示,E,F,G,H,N分别为,,,DA,AB的中点,
则,,
所以平面平面,
所以动点P的轨迹是六边形MEFGHN及其内部.
又因为,所以点在侧面,
所以点的轨迹为线段,
因为AB=AD=2,,
所以.
故选:A.
3.D
【分析】作出几何体直观图,由题意结合几何体体积公式即可得组合体的体积.
【详解】该几何体由直三棱柱及直三棱柱组成,作于M,如图,
因为,所以,
因为重叠后的底面为正方形,所以,
在直棱柱中,平面BHC,则,
由可得平面,
设重叠后的EG与交点为
则
则该几何体的体积为.
故选:D.
4.D
【分析】根据正弦函数的图象特征和性质,结合定义域和值域,即可求解.
【详解】,因为,所以,因为,所以.
正弦函数在一个周期内,要满足上式,则,
所以,所以的取值范围是.
故选:D
5.C
【分析】利用向量的叉乘的定义逐项分析即得.
【详解】解法一:同时与,垂直;,,三个向量构成右手系,
且,所以选项A错误;
根据右手系知:与反向,所以,故选项B错误;
因为,
且与同向共线;
又因为,且与同向共线,
,与同向共线,
所以,且与同向共线,
,故选项C正确;
因为长方体的体积为.
又因为由右手系知向量方向垂直底面向上,与反向,所以,故选项D错误;
故选:C.
解法二:如图建立空间直角坐标系:
,,,
则,所以选项A错误;
,则,故选项D错误;
,故选项B错误;
,则,
,,则.
所以,故选项C正确;
故选:C.
6.D
【分析】设向量与所成角为,二面角的平面角大小为,由平方后求得,取中点E,连接,则,中应用余弦定理求得,两者结合和是与的关系,从而求得结论.
【详解】设向量与所成角为,二面角的平面角大小为,
因为,所以,又,所以,
,,
则,
所以,
取中点E,连接,则,,
,,
在中,,即,
所以,即,
又因为,所以,
因为直线夹角范围为,所以直线与所成角的余弦值范围是.
故选:D.
7.D
【分析】先求得正方体的边长,画出截面,利用向量法证得平面,根据梯形面积公式计算出截面的面积.
【详解】设该正方体外接球的半径为R,
依题意,,解得,故,,故.
分别取棱,的中点F,G,连接,,,,
根据正方体的性质可知:四边形为等腰梯形,
建立如图所示空间直角坐标系,,
,
,
所以,由于,
所以平面,即截面为等腰梯形.
由题可知,,
所以等腰梯形的高为,
故截面图形的面积为
故选:D
8.D
【分析】先求出,转化,列方程即可求出.
【详解】由不共线的平面向量,,两两所成的角相等,可设为θ,则.设||=m.
因为,所以,
即,
所以
即,解得:或3.
所以||=2或3
故选:D
9.AD
【分析】建立空间坐标系,用向量计算异面直线的夹角,做辅助图计算判断相关问题.
【详解】圆弧的圆心的原点,CD为x轴,BA为y轴过圆心O垂直于底面的直线为z轴,建立空间直角坐标系如下图:
则 ,故 ,
所以 ,A正确;
对于B,连接 ,则有则,
∴ 与BC共面,即 四点共面,故B错误;
对于C,设在圆弧 存在一点 ,使得,
则有 , ,此方程组无解,
即E点不存在,故C错误;
对于D,做如下俯视图:
,即以C为球心,为半径的球刚好过A点是球面与底面ABCD唯一的交点,
因为,在球面上,
设与圆弧的交点为,则 ,
解得 ,故,
球面与上底面的交线是以为圆心,半径为1的圆弧 ,则,
圆心角,由图知:,得.
,故D正确;
故选:AD.
10.ABC
【分析】建立空间直角坐标系,利用空间向量计算可得;
【详解】解:如图建立空间直角坐标系,则,,,,,,所以,,,,所以,所以,故A正确;
因为是线段上一动点,所以,所以,所以,当且仅当时,故B正确;
设平面的法向量为,则,即,令,则,所以,因为,即,因为平面,所以平面,故C正确;
设直线与所成的角为,因为,当在线段的端点处时,,在线段的中点时,,所以,故D错误;
故选:ABC
11.ABD
【分析】对于A,证明,根据线面垂直的判定定理可得平面,再根据线面垂直的性质可得,即可判断A;
对于B,证明平面,可得,再根据求出体积,即可判断B;
对于C,以为原点建立空间直角坐标系,利用向量法证明不垂直,即可判断C;
对于D,连接,则线段即为直三棱柱外接球的直径,求出外接球的半径,即可求出外接球面积,即可判断.
【详解】解:对于A,在矩形中,
因为,,D是棱的中点,
所以,
所以,
所以,
又因,,
所以平面,
又因平面,
所以,
即直线与BC所成角为90°,故A正确;
对于B,在直三棱柱中,,
又,,
所以平面,
又平面,所以,
则,故B正确;
对于C,由AB可知,两两垂直,
如图,以为原点建立空间直角坐标系,
则,
则,
所以,
所以不垂直,
所以不垂直平面,故C错误;
连接,则线段即为直三棱柱外接球的直径,
,所以外接球的半径,
所以直三棱柱外接球的表面积为,故D正确.
故选:ABD.
12.BC
【分析】易知摩天轮离地面最近的距离,从而可判断A;求出分钟后,转过的角度,即可求出关于的表达式,即可判断B;由余弦型函数的性质可求出的最小值即可判断C;求出在上的单调性,结合当时,即可判断D.
【详解】解:由题意知,摩天轮离地面最近的距离为米,故A不正确;
分钟后,转过的角度为,则,B正确;
周期为,由余弦型函数的性质可知,若取最小值,
则,又高度相等,则关于对称,则,则;
令,解得,令,解得,
则在上单调递增,在上单调递减,当时,,
当时,,所以在只有一个解;
故选:BC.
【点睛】关键点睛:
本题的关键是求出关于的表达式,结合三角函数的性质进行判断.
13.
【分析】连接,然后可得,,,四点共面,连接,,,设,,连接,然后可得点的运动轨迹为,然后以为坐标原点,,,所在直线分别为,,轴建立空间直角坐标系,然后根据条件求出点的坐标即可.
【详解】连接,因为,分别为棱,的中点,所以,
则,,,四点共面,连接,,,设,,
连接,平面平面,
所以当点在线段上运动时,点的运动轨迹为.
以为坐标原点,,,所在直线分别为,,轴建立如图所示的空间直角坐标系,
由,,得.易得,且,
过点作,交于点,易得,,
则,从而可得,所以,
所以
故答案为:
14.
【分析】由三角形重心的性质和向量的三角形法则得出,再由向量数量积的运算律计算可得.
【详解】解:如图所示,连接并延长与相交于点.
点是底面的重心,
,
又,
则
.
故答案为:.
15.4
【分析】根据给定条件,利用空间向量数量积的性质及运算律计算作答.
【详解】依题意,,且有,而,
所以.
故答案为:4
16.①③
【分析】以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间中两点间的距离公式、二次函数的基本性质可判断①的正误,证明、、不共面可判断②的正误,利用空间向量法可判断③的正误,利用二面角的定义可判断④的正误.
【详解】因为平面平面,平面平面,,平面,平面,
因为,以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,
则、、、、、、、.
对于①,,
当且仅当时,等号成立,①正确;
对于②,当时,,,
,,,
设,即,该方程组无解,所以,②错误;
对于③,、.
,平面的一个法向量为,
,则,平面,平面,③正确;
对于④,当时,、.
设平面的法向量为,,,
由,得,取,可得,
设平面的法向量为,,,
由,得,取,可得,
所以,,此时,二面角不是直二面角,④错误.
故答案为:①③.
【点睛】结论点睛:利用空间向量法处理平行与垂直问题:设直线、的方向向量分别为,,平面、的法向量分别为,.
(1),,
;
(2);
(3),;
(4);
(5),,;
(6).
17.(1);(2);(3).
【分析】(1)以A为原点,射线、、分别为x、y、z轴的非负半轴建立空间直角坐标系,利用空间向量即可求A到平面的距离;
(2)利用(1)中相关信息,再求出平面的法向量即可计算作答;
(3)设出点E的坐标,利用空间向量求异面直线夹角公式列式计算得解
【详解】(1)在四棱锥中,平面,,
以A为原点,射线、、分别为x、y、z轴的非负半轴建立空间直角坐标系,如图,
因,则,
于是得.
设为平面的一个法向量,则,令,得,
所以A到平面的距离;
(2)由(1)知,平面的一个法向量,而平面的一个法向量,
于是得,显然平面与平面夹角为锐角,
所以平面与平面夹角的余弦值是;
(3)因E为棱上的点,设,则,而,
又异面直线与所成的角为,则,解得,
所以的长为.
18.(1)见解析
(2)
(3)
【分析】(1)取的中点为,连接,可证平面平面,从而得到要求证的线面平行.
(2)在平面中,过作的垂线,与交于,则可建立如图所示的空间直角坐标系,求出及平面的法向量后可求线面角的正弦值,进而可得余弦值.
(3)求出平面的法向量与平面的法向量的夹角的余弦值后可求面面角的正弦值.
(1)
取的中点为,连接,
在菱形中,因为,则,
而平面,平面,故平面,
由四棱台可得,而,
故,故,故四边形为平行四边形,
故,而平面,平面,故平面,
因为, 平面,平面,
故平面平面,而平面,故平面.
(2)
在平面中,过作的垂线,与交于,
因为平面,平面,故,
同理,故可建立如图所示的空间直角坐标系,
故,
,
故,,所以,
所以,故,
而平面的一个法向量为,
设直线与平面所成的角为,
则,所以.
(3)
由可得,
故,而,
设平面的法向量为,
则即,取,则,
故,
结合(2)的平面的一个法向量为,
故,
设平面与平面的夹角为,则.
故平面与平面的夹角的正弦值为.
19.(1)证明见解析
(2)
【分析】(1) 取的中点G,连接EG,FG,AC,可证明四边形AGFC是平行四边形,从而证明平面平面ABCD,从而得证.
(2)题意知CA,CB,两两垂直,以C为坐标原点,分别以CA,CB,所在直线为x,y,z轴建立空间直角坐标系,利用向量法求解即可.
(1)
取的中点G,连接EG,FG,AC,
因为,平面ABCD,平面ABCD,
所以平面ABCD,
因为,,所以四边形AGFC是平行四边形,
,又平面ABCD,平面ABCD,
所以平面ABCD,
因为,所以平面平面ABCD,
因为平面ABCD,所以平面ABCD.
(2)
设,
由,得,
因为,所以,
由题意知CA,CB,两两垂直,以C为坐标原点,分别以CA,CB,所在直线为x,y,z轴建立空间直角坐标系,
则,,,,,,
所以,,
设平面的一个法向量为,
由得,取,得,
连接BD,因为,,,所以平面,
所以平面的一个法向量为,
所以,
所以平面与平面所成锐二面角的余弦值为.
20.(1)证明见解析
(2)
【分析】(1)先证明平面得,再根据几何关系得,进而得平面,最后结合判定定理即可证明;
(2)根据题意,以为原点,分别以,的方向为轴、轴的正方向建立如图所示的空间直角坐标系,利用坐标法求解即可.
(1)
证明:因为圆所在的平面,即平面,
而平面,所以.
因为是圆的直径,为圆周上一点,
所以.
又,
所以平面,而平面,
则,
因为,,
所以.又,
所以,而为线段的中点,
所以.
又,
所以平面,
而平面,故平面平面.
(2)
解:以为原点,分别以,的方向为轴、轴的正方向建立如图所示的空间直角坐标系.
不妨设,则,,,,,.
设平面的法向量为,
则令,得.
由(1)知平面的一个法向量为,
设二面角为,易知为锐角,则,
即二面角的余弦值为.
21.(1);(2).
【分析】(1)首先证得,由此求得的值.
(2)利用平面和平面的法向量计算出二面角的余弦值.
【详解】(1)因为,且,
所以,从而,
因为平面,
平面,
平面平面,
所以,
所以.
(2)以点A为坐标原点 方向为y轴正方向 方向为z轴正方向,建立如图所示
的空间直角坐标系,则,,,,
由(1)知,解得,
所以,,
设平面法向量为,则
,,令,得,
平面的法向量为,
所以,
由图可知二面角的平面角为钝角,
所以二面角的余弦值为.
【点睛】在求二面角的余弦值时,要注意首先判断二面角的平面角是锐角还是钝角.
22.(1)证明见解析
(2)
【分析】(1)利用平行四边形可证,可得,再由,即可求证;
(2)建立空间直角坐标系,利用向量法求解.
(1)
取的中点,连接,,
因为是等边的中线,所以
因为是棱的中点,为的中点,
所以,且
因为,,所以,且,
所以四边形是平行四边形,所以.
因为,为的中点,所以,从而.
又,且平面,平面,
所以平面.
(2)
由(1)知,又,,且 平面,
所以面,从而平面.
以为坐标原点,,,的方向分别为,,轴的正方向,
建立如图所示的空间直角坐标系.
则,,,
所以,,
设平面的法向量为,
由得
令,则,,所以.
又平面的一个法向量为,
所以,
即平面与平面夹角的余弦值为.
答案第1页,共2页
答案第1页,共2页
1.已知正四棱台的上、下底面边长分别为1和2,P是上底面的边界上一点.若的最小值为,则该正四棱台的体积为( )
A. B.3 C. D.1
2.已知长方体,,,M是的中点,点P满足,其中,,且平面,则动点P的轨迹所形成的轨迹长度是( )
A. B. C. D.2
3.如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为,腰为3的等腰三角形,则该几何体的体积为( )
A.23 B.24 C.26 D.27
4.已知函数的定义域为,值域为,则的取值范围是( )
A. B.
C. D.
5.向量的运算包含点乘和叉乘,其中点乘就是大家熟悉的向量的数量积.现定义向量的叉乘:给定两个不共线的空间向量与,规定:①为同时与,垂直的向量;②,,三个向量构成右手系(如图1);③;④若,,则,其中.如图2,在长方体中,,,则下列结论正确的是( )
A.
B.
C.
D.长方体的体积
6.如图,四边形中,.现将沿折起,当二面角处于过程中,直线与所成角的余弦值取值范围是( )
A. B. C. D.
7.已知正方体的外接球表面积为,点E为棱的中点,且平面,点平面,则平面截正方体所得的截面图形的面积为( )
A. B. C. D.
8.已知不共线的平面向量两两所成的角相等,且,则( )
A. B.2 C.3 D.2或3
二、多选题
9.中国古代数学著作《九章算术》中,记载了一种称为“曲池”的几何体,该几何体的上下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分),现有一个如图所示的曲池,它的高为2,,,,均与曲池的底面垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为90°,则以下命题正确的是( )
A.与成角的余弦值为
B.,,,四点不共面
C.弧上存在一点,使得
D.以点为球心,为半径的球面与曲池上底面的交线长为
10.如图,正方体的棱长为1,P是线段上的动点,则下列结论中正确的是( )
A.
B.的最小值为
C.平面
D.异面直线与,所成角的取值范围是
11.如图,在直三棱柱中,,,D是棱的中点,,点E在上,且,则下列结论正确的是( )
A.直线与BC所成角为90°
B.三棱锥的体积为
C.平面
D.直三棱柱外接球的表面积为
12.摩天轮常被当作一个城市的地标性建筑,如深圳前海的“湾区之光”摩天轮,如图所示,某摩天轮最高点离地面高度128米,转盘直径为120米,设置若干个座舱,游客从离地面最近的位置进舱,开启后按逆时针匀速旋转分钟,当时,游客随舱旋转至距离地面最远处.以下关于摩天轮的说法中,正确的为( )
A.摩天轮离地面最近的距离为4米
B.若旋转分钟后,游客距离地面的高度为米,则
C.若在,时刻,游客距离地面的高度相等,则的最小值为30
D.,,使得游客在该时刻距离地面的高度均为90米
三、填空题
13.在长方体中,底面是边长为的正方形,,,分别为棱,的中点,为线段上的动点,则直线与平面的交点的轨迹长度为______.
14.在四面体中,棱,,两两垂直,且,,,为的重心,则______.
15.二面角为,A,B是棱l上的两点,,分别在半平面内,,,且,,则的长_______________.
16.如图,边长为的正方形所在平面与正方形所在平面互相垂直,动点、分别在正方形对角线和上移动,且.则下列结论:
①长度的最小值为;
②当时,与相交;
③始终与平面平行;
④当时,为直二面角.
正确的序号是__________.
四、解答题
17.如图,在四棱锥中,平面,.
(1)求A到平面的距离;
(2)求平面与平面夹角的余弦值;
(3)设E为棱上的点,满足异面直线与所成的角为,求的长.
18.如图,在四棱台中,底面四边形ABCD为菱形,平面.
(1)若点是的中点,求证:平面
(2)求直线与平面所成角的余弦值;
(3)棱上存在点,使得,求平面与平面的夹角的正弦值.
19.如图所示的圆柱中,AB是圆O的直径,,为圆柱的母线,四边形ABCD是底面圆O的内接等腰梯形,且,E,F分别为,的中点.
(1)证明:平面ABCD;
(2)求平面与平面所成锐二面角的余弦值.
20.如图,是圆的直径,圆所在的平面,为圆周上一点,为线段的中点,,.
(1)证明:平面平面.
(2)若为的中点,求二面角的余弦值.
21.如图,平面,,,,四边形的对角线交于点M,N为棱上一点,且平面.
(1)求的值:
(2)求二面角的余弦值.
22.如图,在四棱锥P ABCD中,已知AB∥CD,AD⊥CD,BC=BP,CD=2AB=4,△ADP是等边三角形,E为DP的中点.
(1)证明:AE⊥平面PCD;
(2)若,求平面PBC与平面PAD夹角的余弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据题意建立空间直角坐标系,写出相应点的坐标,利用空间向量的数量积的坐标公式及二次函数的性质及已知得出正四棱台的高,
再结合棱台的体积公式即可求解.
【详解】由题意可知,以为坐标原点,所在直线分别为轴,建立空间直角坐标系,如图所示
,,由对称性,点在是相同的,
故只考虑在上时,设正四棱台的高为,则
,,
设,,
因为在上,所以,则
,
,
所以
由二次函数的性质知,当时,取得最小值为,
又因为的最小值为,所以,解得(负舍),
故正四棱台的体积为
.
故选:A.
2.A
【分析】先构造和平面平行的截面,再根据空间向量共面确定点的轨迹形状,再求其长度.
【详解】如图所示,E,F,G,H,N分别为,,,DA,AB的中点,
则,,
所以平面平面,
所以动点P的轨迹是六边形MEFGHN及其内部.
又因为,所以点在侧面,
所以点的轨迹为线段,
因为AB=AD=2,,
所以.
故选:A.
3.D
【分析】作出几何体直观图,由题意结合几何体体积公式即可得组合体的体积.
【详解】该几何体由直三棱柱及直三棱柱组成,作于M,如图,
因为,所以,
因为重叠后的底面为正方形,所以,
在直棱柱中,平面BHC,则,
由可得平面,
设重叠后的EG与交点为
则
则该几何体的体积为.
故选:D.
4.D
【分析】根据正弦函数的图象特征和性质,结合定义域和值域,即可求解.
【详解】,因为,所以,因为,所以.
正弦函数在一个周期内,要满足上式,则,
所以,所以的取值范围是.
故选:D
5.C
【分析】利用向量的叉乘的定义逐项分析即得.
【详解】解法一:同时与,垂直;,,三个向量构成右手系,
且,所以选项A错误;
根据右手系知:与反向,所以,故选项B错误;
因为,
且与同向共线;
又因为,且与同向共线,
,与同向共线,
所以,且与同向共线,
,故选项C正确;
因为长方体的体积为.
又因为由右手系知向量方向垂直底面向上,与反向,所以,故选项D错误;
故选:C.
解法二:如图建立空间直角坐标系:
,,,
则,所以选项A错误;
,则,故选项D错误;
,故选项B错误;
,则,
,,则.
所以,故选项C正确;
故选:C.
6.D
【分析】设向量与所成角为,二面角的平面角大小为,由平方后求得,取中点E,连接,则,中应用余弦定理求得,两者结合和是与的关系,从而求得结论.
【详解】设向量与所成角为,二面角的平面角大小为,
因为,所以,又,所以,
,,
则,
所以,
取中点E,连接,则,,
,,
在中,,即,
所以,即,
又因为,所以,
因为直线夹角范围为,所以直线与所成角的余弦值范围是.
故选:D.
7.D
【分析】先求得正方体的边长,画出截面,利用向量法证得平面,根据梯形面积公式计算出截面的面积.
【详解】设该正方体外接球的半径为R,
依题意,,解得,故,,故.
分别取棱,的中点F,G,连接,,,,
根据正方体的性质可知:四边形为等腰梯形,
建立如图所示空间直角坐标系,,
,
,
所以,由于,
所以平面,即截面为等腰梯形.
由题可知,,
所以等腰梯形的高为,
故截面图形的面积为
故选:D
8.D
【分析】先求出,转化,列方程即可求出.
【详解】由不共线的平面向量,,两两所成的角相等,可设为θ,则.设||=m.
因为,所以,
即,
所以
即,解得:或3.
所以||=2或3
故选:D
9.AD
【分析】建立空间坐标系,用向量计算异面直线的夹角,做辅助图计算判断相关问题.
【详解】圆弧的圆心的原点,CD为x轴,BA为y轴过圆心O垂直于底面的直线为z轴,建立空间直角坐标系如下图:
则 ,故 ,
所以 ,A正确;
对于B,连接 ,则有则,
∴ 与BC共面,即 四点共面,故B错误;
对于C,设在圆弧 存在一点 ,使得,
则有 , ,此方程组无解,
即E点不存在,故C错误;
对于D,做如下俯视图:
,即以C为球心,为半径的球刚好过A点是球面与底面ABCD唯一的交点,
因为,在球面上,
设与圆弧的交点为,则 ,
解得 ,故,
球面与上底面的交线是以为圆心,半径为1的圆弧 ,则,
圆心角,由图知:,得.
,故D正确;
故选:AD.
10.ABC
【分析】建立空间直角坐标系,利用空间向量计算可得;
【详解】解:如图建立空间直角坐标系,则,,,,,,所以,,,,所以,所以,故A正确;
因为是线段上一动点,所以,所以,所以,当且仅当时,故B正确;
设平面的法向量为,则,即,令,则,所以,因为,即,因为平面,所以平面,故C正确;
设直线与所成的角为,因为,当在线段的端点处时,,在线段的中点时,,所以,故D错误;
故选:ABC
11.ABD
【分析】对于A,证明,根据线面垂直的判定定理可得平面,再根据线面垂直的性质可得,即可判断A;
对于B,证明平面,可得,再根据求出体积,即可判断B;
对于C,以为原点建立空间直角坐标系,利用向量法证明不垂直,即可判断C;
对于D,连接,则线段即为直三棱柱外接球的直径,求出外接球的半径,即可求出外接球面积,即可判断.
【详解】解:对于A,在矩形中,
因为,,D是棱的中点,
所以,
所以,
所以,
又因,,
所以平面,
又因平面,
所以,
即直线与BC所成角为90°,故A正确;
对于B,在直三棱柱中,,
又,,
所以平面,
又平面,所以,
则,故B正确;
对于C,由AB可知,两两垂直,
如图,以为原点建立空间直角坐标系,
则,
则,
所以,
所以不垂直,
所以不垂直平面,故C错误;
连接,则线段即为直三棱柱外接球的直径,
,所以外接球的半径,
所以直三棱柱外接球的表面积为,故D正确.
故选:ABD.
12.BC
【分析】易知摩天轮离地面最近的距离,从而可判断A;求出分钟后,转过的角度,即可求出关于的表达式,即可判断B;由余弦型函数的性质可求出的最小值即可判断C;求出在上的单调性,结合当时,即可判断D.
【详解】解:由题意知,摩天轮离地面最近的距离为米,故A不正确;
分钟后,转过的角度为,则,B正确;
周期为,由余弦型函数的性质可知,若取最小值,
则,又高度相等,则关于对称,则,则;
令,解得,令,解得,
则在上单调递增,在上单调递减,当时,,
当时,,所以在只有一个解;
故选:BC.
【点睛】关键点睛:
本题的关键是求出关于的表达式,结合三角函数的性质进行判断.
13.
【分析】连接,然后可得,,,四点共面,连接,,,设,,连接,然后可得点的运动轨迹为,然后以为坐标原点,,,所在直线分别为,,轴建立空间直角坐标系,然后根据条件求出点的坐标即可.
【详解】连接,因为,分别为棱,的中点,所以,
则,,,四点共面,连接,,,设,,
连接,平面平面,
所以当点在线段上运动时,点的运动轨迹为.
以为坐标原点,,,所在直线分别为,,轴建立如图所示的空间直角坐标系,
由,,得.易得,且,
过点作,交于点,易得,,
则,从而可得,所以,
所以
故答案为:
14.
【分析】由三角形重心的性质和向量的三角形法则得出,再由向量数量积的运算律计算可得.
【详解】解:如图所示,连接并延长与相交于点.
点是底面的重心,
,
又,
则
.
故答案为:.
15.4
【分析】根据给定条件,利用空间向量数量积的性质及运算律计算作答.
【详解】依题意,,且有,而,
所以.
故答案为:4
16.①③
【分析】以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间中两点间的距离公式、二次函数的基本性质可判断①的正误,证明、、不共面可判断②的正误,利用空间向量法可判断③的正误,利用二面角的定义可判断④的正误.
【详解】因为平面平面,平面平面,,平面,平面,
因为,以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,
则、、、、、、、.
对于①,,
当且仅当时,等号成立,①正确;
对于②,当时,,,
,,,
设,即,该方程组无解,所以,②错误;
对于③,、.
,平面的一个法向量为,
,则,平面,平面,③正确;
对于④,当时,、.
设平面的法向量为,,,
由,得,取,可得,
设平面的法向量为,,,
由,得,取,可得,
所以,,此时,二面角不是直二面角,④错误.
故答案为:①③.
【点睛】结论点睛:利用空间向量法处理平行与垂直问题:设直线、的方向向量分别为,,平面、的法向量分别为,.
(1),,
;
(2);
(3),;
(4);
(5),,;
(6).
17.(1);(2);(3).
【分析】(1)以A为原点,射线、、分别为x、y、z轴的非负半轴建立空间直角坐标系,利用空间向量即可求A到平面的距离;
(2)利用(1)中相关信息,再求出平面的法向量即可计算作答;
(3)设出点E的坐标,利用空间向量求异面直线夹角公式列式计算得解
【详解】(1)在四棱锥中,平面,,
以A为原点,射线、、分别为x、y、z轴的非负半轴建立空间直角坐标系,如图,
因,则,
于是得.
设为平面的一个法向量,则,令,得,
所以A到平面的距离;
(2)由(1)知,平面的一个法向量,而平面的一个法向量,
于是得,显然平面与平面夹角为锐角,
所以平面与平面夹角的余弦值是;
(3)因E为棱上的点,设,则,而,
又异面直线与所成的角为,则,解得,
所以的长为.
18.(1)见解析
(2)
(3)
【分析】(1)取的中点为,连接,可证平面平面,从而得到要求证的线面平行.
(2)在平面中,过作的垂线,与交于,则可建立如图所示的空间直角坐标系,求出及平面的法向量后可求线面角的正弦值,进而可得余弦值.
(3)求出平面的法向量与平面的法向量的夹角的余弦值后可求面面角的正弦值.
(1)
取的中点为,连接,
在菱形中,因为,则,
而平面,平面,故平面,
由四棱台可得,而,
故,故,故四边形为平行四边形,
故,而平面,平面,故平面,
因为, 平面,平面,
故平面平面,而平面,故平面.
(2)
在平面中,过作的垂线,与交于,
因为平面,平面,故,
同理,故可建立如图所示的空间直角坐标系,
故,
,
故,,所以,
所以,故,
而平面的一个法向量为,
设直线与平面所成的角为,
则,所以.
(3)
由可得,
故,而,
设平面的法向量为,
则即,取,则,
故,
结合(2)的平面的一个法向量为,
故,
设平面与平面的夹角为,则.
故平面与平面的夹角的正弦值为.
19.(1)证明见解析
(2)
【分析】(1) 取的中点G,连接EG,FG,AC,可证明四边形AGFC是平行四边形,从而证明平面平面ABCD,从而得证.
(2)题意知CA,CB,两两垂直,以C为坐标原点,分别以CA,CB,所在直线为x,y,z轴建立空间直角坐标系,利用向量法求解即可.
(1)
取的中点G,连接EG,FG,AC,
因为,平面ABCD,平面ABCD,
所以平面ABCD,
因为,,所以四边形AGFC是平行四边形,
,又平面ABCD,平面ABCD,
所以平面ABCD,
因为,所以平面平面ABCD,
因为平面ABCD,所以平面ABCD.
(2)
设,
由,得,
因为,所以,
由题意知CA,CB,两两垂直,以C为坐标原点,分别以CA,CB,所在直线为x,y,z轴建立空间直角坐标系,
则,,,,,,
所以,,
设平面的一个法向量为,
由得,取,得,
连接BD,因为,,,所以平面,
所以平面的一个法向量为,
所以,
所以平面与平面所成锐二面角的余弦值为.
20.(1)证明见解析
(2)
【分析】(1)先证明平面得,再根据几何关系得,进而得平面,最后结合判定定理即可证明;
(2)根据题意,以为原点,分别以,的方向为轴、轴的正方向建立如图所示的空间直角坐标系,利用坐标法求解即可.
(1)
证明:因为圆所在的平面,即平面,
而平面,所以.
因为是圆的直径,为圆周上一点,
所以.
又,
所以平面,而平面,
则,
因为,,
所以.又,
所以,而为线段的中点,
所以.
又,
所以平面,
而平面,故平面平面.
(2)
解:以为原点,分别以,的方向为轴、轴的正方向建立如图所示的空间直角坐标系.
不妨设,则,,,,,.
设平面的法向量为,
则令,得.
由(1)知平面的一个法向量为,
设二面角为,易知为锐角,则,
即二面角的余弦值为.
21.(1);(2).
【分析】(1)首先证得,由此求得的值.
(2)利用平面和平面的法向量计算出二面角的余弦值.
【详解】(1)因为,且,
所以,从而,
因为平面,
平面,
平面平面,
所以,
所以.
(2)以点A为坐标原点 方向为y轴正方向 方向为z轴正方向,建立如图所示
的空间直角坐标系,则,,,,
由(1)知,解得,
所以,,
设平面法向量为,则
,,令,得,
平面的法向量为,
所以,
由图可知二面角的平面角为钝角,
所以二面角的余弦值为.
【点睛】在求二面角的余弦值时,要注意首先判断二面角的平面角是锐角还是钝角.
22.(1)证明见解析
(2)
【分析】(1)利用平行四边形可证,可得,再由,即可求证;
(2)建立空间直角坐标系,利用向量法求解.
(1)
取的中点,连接,,
因为是等边的中线,所以
因为是棱的中点,为的中点,
所以,且
因为,,所以,且,
所以四边形是平行四边形,所以.
因为,为的中点,所以,从而.
又,且平面,平面,
所以平面.
(2)
由(1)知,又,,且 平面,
所以面,从而平面.
以为坐标原点,,,的方向分别为,,轴的正方向,
建立如图所示的空间直角坐标系.
则,,,
所以,,
设平面的法向量为,
由得
令,则,,所以.
又平面的一个法向量为,
所以,
即平面与平面夹角的余弦值为.
答案第1页,共2页
答案第1页,共2页
