2022-2023学年人教版数学九年级上册24.3正多边形和圆(2)课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册24.3正多边形和圆(2)课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 21:09:44 | ||
图片预览






文档简介
(共19张PPT)
24.3正多边形和圆(第2课时)
第二十四章 圆
学习目标
1.进一步理解并掌握正多边形半径和边长、边心距、中心角之间的关系
2.掌握圆内接正多边形的两种画法:
(1)用量角器等分圆周法作正多边形;
(2)用尺规作图法作特殊的正多边形
01
新课导入
新课导入
实际生活中,经常遇到画正多边形的问题,比如画一个六角螺帽的平面图、画一个五角星等,这些问题都与等分圆周有关,要制造下图中的零件,也需要等分圆周.
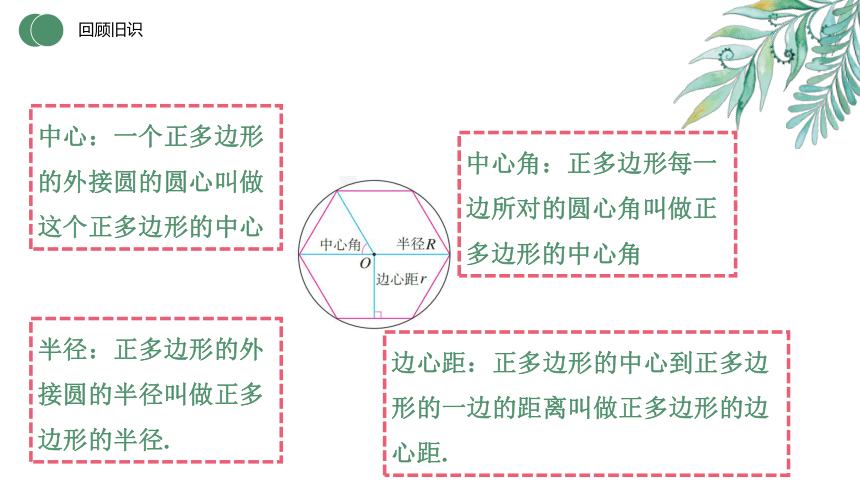
回顾旧识
中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心
半径:正多边形的外接圆的半径叫做正多边形的半径.
中心角:正多边形每一边所对的圆心角叫做正多边形的中心角
边心距:正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
回顾旧识
正多边形和圆有怎样的关系?
正n边形的一个内角的度数是 ;中心角是 ;中心角和外角的关系是 .
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
相等
02
探索新知
问题1
怎样等分圆周?
分析:因为同圆中相等的圆心角所对的弧相等,所以作相等的圆心角就可以等分圆,从而得到相应的正多边形.
利用你手中的工具,画一个边长为2cm的正六边形.
画一画
第一种方法,如图,以2cm为半径作一个 ,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
·
60°
O
90
0
180
60
120
利用这种方法可以画出任意的正n边形.
画一个边长为2cm的正六边形
及时练
第二种方法,如图,以2cm为半径作一个⊙O,由于正六边形的
半径等于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺次连接各分点即可.
·
O
由此,你能画出正三角形,正十二边形吗
问题
小结:如何用等分圆周的方法画正多边形?
一、度量法:依次画出相等的圆心角来等分圆
这种方法比较准确,但是麻烦
二、尺规法:在半径为R的圆中,先用量角器画一个等于 的圆心角,这个角所对的弧就是圆中的 ,然后在院上依次截取这条弧的等弧,就得到圆的n等分点,顺次连接各等分点从而作出半径为R的正n边形
此方法可将圆任意n等分,所以用该方法可作出任意正多边形,但边数很大时,容易产生较大的误差.
画一画
正四边形:如下图所示,在 中用直尺和圆规作两条互相垂直的直径,就可以把 四等分,从而作出正四边形;
正八边形:再用直尺和圆规分别作与正四边形相邻两边垂直的直径,就可以作出正八边形,如上图所示.
正十六边形:同理可以作出正十六边形等边数逐次倍增的正多边形.
动手试一试
画一画
正六边形:如下图所以,先画 的任意一条直径AB,再
分别以点A,B为圆心,以 的半径R为半径画弧,与 相交于点C,D和E,F,顺次连接点A,C,E,B,F,D,A,得正六边形ACEBFD;
正十二边形:在正六边形的基础上可作正十二边形,如右图所示;
画一画
正三角形:连接BD,BC,CD,得正三角形,如下图所示.
我们不难发现,随着边数的增加,正多边形越来越接近于圆,正多边形将越来越难画
作圆 确定圆心角 所对的弧 截取等弧 顺次连接各分点 正多边形
03
练习
练习
练习
04
小结
小结
1.本节课我们主要学习了哪些内容?
2.用量角器等分圆
3.尺规作图等分圆
24.3正多边形和圆(第2课时)
第二十四章 圆
学习目标
1.进一步理解并掌握正多边形半径和边长、边心距、中心角之间的关系
2.掌握圆内接正多边形的两种画法:
(1)用量角器等分圆周法作正多边形;
(2)用尺规作图法作特殊的正多边形
01
新课导入
新课导入
实际生活中,经常遇到画正多边形的问题,比如画一个六角螺帽的平面图、画一个五角星等,这些问题都与等分圆周有关,要制造下图中的零件,也需要等分圆周.
回顾旧识
中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心
半径:正多边形的外接圆的半径叫做正多边形的半径.
中心角:正多边形每一边所对的圆心角叫做正多边形的中心角
边心距:正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
回顾旧识
正多边形和圆有怎样的关系?
正n边形的一个内角的度数是 ;中心角是 ;中心角和外角的关系是 .
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
相等
02
探索新知
问题1
怎样等分圆周?
分析:因为同圆中相等的圆心角所对的弧相等,所以作相等的圆心角就可以等分圆,从而得到相应的正多边形.
利用你手中的工具,画一个边长为2cm的正六边形.
画一画
第一种方法,如图,以2cm为半径作一个 ,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
·
60°
O
90
0
180
60
120
利用这种方法可以画出任意的正n边形.
画一个边长为2cm的正六边形
及时练
第二种方法,如图,以2cm为半径作一个⊙O,由于正六边形的
半径等于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺次连接各分点即可.
·
O
由此,你能画出正三角形,正十二边形吗
问题
小结:如何用等分圆周的方法画正多边形?
一、度量法:依次画出相等的圆心角来等分圆
这种方法比较准确,但是麻烦
二、尺规法:在半径为R的圆中,先用量角器画一个等于 的圆心角,这个角所对的弧就是圆中的 ,然后在院上依次截取这条弧的等弧,就得到圆的n等分点,顺次连接各等分点从而作出半径为R的正n边形
此方法可将圆任意n等分,所以用该方法可作出任意正多边形,但边数很大时,容易产生较大的误差.
画一画
正四边形:如下图所示,在 中用直尺和圆规作两条互相垂直的直径,就可以把 四等分,从而作出正四边形;
正八边形:再用直尺和圆规分别作与正四边形相邻两边垂直的直径,就可以作出正八边形,如上图所示.
正十六边形:同理可以作出正十六边形等边数逐次倍增的正多边形.
动手试一试
画一画
正六边形:如下图所以,先画 的任意一条直径AB,再
分别以点A,B为圆心,以 的半径R为半径画弧,与 相交于点C,D和E,F,顺次连接点A,C,E,B,F,D,A,得正六边形ACEBFD;
正十二边形:在正六边形的基础上可作正十二边形,如右图所示;
画一画
正三角形:连接BD,BC,CD,得正三角形,如下图所示.
我们不难发现,随着边数的增加,正多边形越来越接近于圆,正多边形将越来越难画
作圆 确定圆心角 所对的弧 截取等弧 顺次连接各分点 正多边形
03
练习
练习
练习
04
小结
小结
1.本节课我们主要学习了哪些内容?
2.用量角器等分圆
3.尺规作图等分圆
同课章节目录
